De gemiddelde hoeksnelheid Rotatie wordt gedefinieerd als de hoek die per tijdseenheid wordt geroteerd van de positievector van een punt dat een cirkelvormige beweging beschrijft. De bladen van een plafondventilator (zoals die in figuur 1) volgen een cirkelvormige beweging en hun gemiddelde rotatiesnelheid wordt berekend door het quotiënt te nemen tussen de gedraaide hoek en de tijd waarin die hoek werd afgelegd..
De regels die rotatiebeweging volgt, lijken enigszins op de bekende regels voor translatiebeweging. De afgelegde afstanden kunnen ook in meters worden gemeten, maar de hoekgrootten krijgen een speciale betekenis omdat ze de beschrijving van de beweging aanzienlijk vergemakkelijken..
Over het algemeen worden Griekse letters gebruikt voor de hoekgrootheden en Latijnse letters voor de overeenkomstige lineaire grootheden..
Artikel index
Figuur 2 geeft de beweging weer van een punt op een cirkelvormig pad c. De positie P van het punt komt overeen met het moment t en de hoekpositie die overeenkomt met dat moment is ϕ.
Vanaf het moment t verstrijkt een tijdsperiode Δt. In die periode is de nieuwe positie van het punt P 'en is de hoekpositie met een hoek Δϕ vergroot.
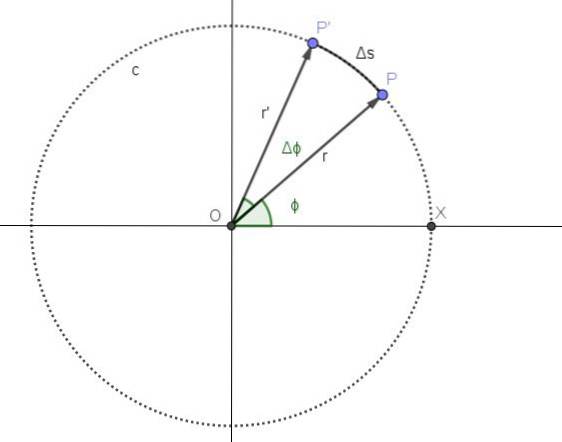
De gemiddelde hoeksnelheid ω is de hoek die per tijdseenheid wordt afgelegd, zodat het quotiënt Δϕ / Δt de gemiddelde hoeksnelheid tussen tijden t en t + Δt vertegenwoordigt:
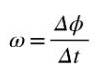
Omdat de hoek wordt gemeten in radialen en de tijd in seconden, is de eenheid voor de gemiddelde hoeksnelheid rad / s. Als u de hoeksnelheid precies op het moment t, dan zullen we het quotiënt Δϕ / Δt moeten berekenen als Δt ➡0.
Een rotatiebeweging is uniform als op elk waargenomen moment de afgelegde hoek dezelfde is in dezelfde tijdsperiode. Als de rotatie uniform is, valt de hoeksnelheid op elk moment samen met de gemiddelde hoeksnelheid.
Bij een uniforme rotatiebeweging wordt de tijd waarin een volledige omwenteling wordt gemaakt de periode en wordt aangegeven met T.
Bovendien, wanneer een volledige bocht is gemaakt, is de afgelegde hoek 2π, dus in een uniforme rotatie is de hoeksnelheid ω gerelateerd aan de periode T, door de volgende formule:
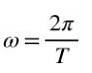
Het definieert de frequentie F. van een uniforme rotatie als het quotiënt tussen het aantal beurten en de tijd die wordt gebruikt om ze te doorlopen, dat wil zeggen, als er N beurten worden gemaakt in de tijdsperiode Δt, dan is de frequentie:
f = N / Δt
Aangezien er één beurt (N = 1) wordt afgelegd in tijd T (de periode), wordt de volgende relatie verkregen:
f = 1 / T
Dat wil zeggen, in een uniforme rotatie is de hoeksnelheid gerelateerd aan de frequentie door de relatie:
ω = 2π ・ f
Lineaire snelheid v, is het quotiënt tussen de afgelegde afstand en de tijd die nodig is om deze af te leggen. In figuur 2 is de afgelegde afstand de booglengte Δs.
De boog Δs is evenredig met de afgelegde hoek Δϕ en de straal r, waarbij aan de volgende relatie is voldaan:
Δs = r ・ Δϕ
Zolang Δϕ wordt gemeten in radialen.
Als we de vorige uitdrukking delen door de tijdsverloop Δt, krijgen we:
(Δs / Δt) = r ・ (Δϕ / Δt)
Het quotiënt van het eerste lid is de lineaire snelheid en het quotiënt van het tweede lid is de gemiddelde hoeksnelheid:
v = r ・ ω
De uiteinden van de bladen van de plafondventilator getoond in figuur 1 bewegen met een snelheid van 5 m / s en de bladen hebben een straal van 40 cm.
Bereken met deze gegevens: i) de gemiddelde hoeksnelheid van het wiel, ii) het aantal omwentelingen dat het wiel maakt in één seconde, iii) de periode in seconden.
i) De lineaire snelheid is v = 5 m / s.
De straal is r = 0,40 m.
Uit de relatie tussen lineaire snelheid en hoeksnelheid lossen we het laatste op:
v = r ・ ω => ω = v / r = (5 m / s) / (0,40 m) = 12,57 rad / s
ii) ω = 2π ・ f => f = ω / 2π = (12,57 rad / s) / (2π rad) = 2 omwentelingen / s
iii) T = 1 / f = 1 / (2 omwentelingen / sec.) = 0,5 s voor elke omwenteling.
Een speelgoedbuggy beweegt op een cirkelvormige baan met een straal van 2 meter. Bij 0s is zijn hoekpositie 0 rad, maar na verloop van tijd t is zijn hoekpositie
φ (t) = 2 ・ t .
Met deze gegevens
i) Bereken de gemiddelde hoeksnelheid in de volgende tijdsintervallen [0s, 0,5s]; [0,5 s, 1,0 s]; [1.0s, 1.5s] en tot slot in de periode [0.0s, 1.5s].
ii) Gebaseerd op de resultaten van deel i) Wat kan er gezegd worden over de beweging?
iii) Bepaal de gemiddelde lineaire snelheid in dezelfde tijdsperiode uit deel i)
iv) Vind de hoeksnelheid en lineaire snelheid voor elk moment.
i) De gemiddelde hoeksnelheid wordt gegeven door de volgende formule:
We gaan verder met het berekenen van de afgelegde hoek en het tijdsverloop dat in elk interval is verstreken.
Interval 1: Δϕ = ϕ (0,5 s) - ϕ (0,0 s) = 2 (rad / s) * 0,5 s - 2 (rad / s) * 0,0 s = 1,0 rad
Δt = 0,5 s - 0,0 s = 0,5 s
ω = Δϕ / Δt = 1,0 rad / 0,5 s = 2,0 rad / s
Interval 2: Δϕ = ϕ (1,0 s) - ϕ (0,5 s) = 2 (rad / s) * 1,0 s - 2 (rad / s) * 0,5 s = 1,0 rad
Δt = 1,0 s - 0,5 s = 0,5 s
ω = Δϕ / Δt = 1,0 rad / 0,5 s = 2,0 rad / s
Interval 3: Δϕ = ϕ (1,5 s) - ϕ (1,0 s) = 2 (rad / s) * 1,5 s - 2 (rad / s) * 1,0 s = 1,0 rad
Δt = 1,5 s - 1,0 s = 0,5 s
ω = Δϕ / Δt = 1,0 rad / 0,5 s = 2,0 rad / s
Interval 4: Δϕ = ϕ (1,5 s) - ϕ (0,0 s) = 2 (rad / s) * 1,5 s - 2 (rad / s) * 0,0 s = 3,0 rad
Δt = 1,5 s - 0,0 s = 1,5 s
ω = Δϕ / Δt = 3.0 rad / 1.5s = 2.0 rad / s
ii) Gezien de eerdere resultaten, waarin de gemiddelde hoeksnelheid werd berekend in verschillende tijdsintervallen, waarbij altijd hetzelfde resultaat werd verkregen, lijkt het erop te wijzen dat het een uniforme cirkelvormige beweging is. Deze resultaten zijn echter niet overtuigend..
De manier om tot de conclusie te komen, is door de gemiddelde hoeksnelheid te berekenen voor een willekeurig interval [t, t ']: Δϕ = ϕ (t') - ϕ (t) = 2 * t '- 2 * t = 2 * (t '-t)
Δt = t '- t
ω = Δϕ / Δt = 2 * (t'-t) / (t'-t) = 2,0 rad / s
Dit betekent dat de speelgoedbuggy een constante gemiddelde hoeksnelheid van 2 rad / s heeft in elke beschouwde tijdsperiode. Maar je kunt verder gaan als je de momentane hoeksnelheid berekent:
Dit wordt geïnterpreteerd als dat de speelgoedauto te allen tijde een constante hoeksnelheid = 2 rad / s heeft.
Niemand heeft nog op dit artikel gereageerd.