
Areolaire snelheid hoe het wordt berekend en oefeningen worden opgelost
De areolaire snelheid is het geveegde oppervlak per tijdseenheid en is constant. Het is specifiek voor elke planeet en komt voort uit de beschrijving van de tweede wet van Kepler in wiskundige vorm. In dit artikel leggen we uit wat het is en hoe het wordt berekend.
De hausse die de ontdekking van planeten buiten het zonnestelsel vertegenwoordigt, heeft de belangstelling voor planetaire beweging nieuw leven ingeblazen. Niets suggereert dat deze exoplaneten andere wetten volgen dan die al bekend en geldig zijn in het zonnestelsel: de wetten van Kepler..
Johannes Kepler was de astronoom die, zonder de hulp van de telescoop en met behulp van de waarnemingen van zijn mentor Tycho Brahe, een wiskundig model creëerde dat de beweging van de planeten rond de zon beschrijft..
Hij verliet dit model, belichaamd in de drie wetten die zijn naam dragen en die nog steeds even geldig zijn als in 1609, toen hij de eerste twee vaststelde en in 1618, de datum waarop hij de derde uitsprak..
Artikel index
- 1 De wetten van Kepler
- 2 Waarom bewegen de planeten elliptisch rond de zon??
- 3 De grootte van de lineaire snelheid van een planeet is niet constant
- 4 Areolaire snelheid
- 5 Berekenen van lineaire snelheid en areolaire snelheid
- 5.1 Oefening
- 6 Bibliografie
Kepler's wetten
In het huidige spraakgebruik luiden de drie wetten van Kepler als volgt:
1. De banen van alle planeten zijn elliptisch en de zon staat in focus.
2. De positievector van de zon naar een planeet veegt in gelijke tijden over gelijke gebieden.
3. Het kwadraat van de omlooptijd van een planeet is evenredig met de kubus van de halve hoofdas van de beschreven ellips..
Een planeet heeft een lineaire snelheid, net als elk bekend bewegend object. En er is zelfs meer: bij het schrijven van de tweede wet van Kepler in wiskundige vorm, ontstaat een nieuw concept dat areolaire snelheid wordt genoemd, typerend voor elke planeet..
Waarom bewegen de planeten elliptisch rond de zon??
De aarde en de andere planeten bewegen rond de zon dankzij het feit dat het een kracht op hen uitoefent: de zwaartekracht. Hetzelfde gebeurt met elke andere ster en de planeten waaruit het systeem bestaat, als die er zijn..
Dit is een kracht van het type dat bekend staat als een centrale kracht. Gewicht is een centrale kracht die iedereen kent. Het object dat de centrale kracht uitoefent, of het nu de zon is of een verre ster, trekt de planeten naar het midden en ze bewegen in een gesloten curve.
In principe kan deze curve worden benaderd als een omtrek, net als Nicolás Copernicus, een Poolse astronoom die de heliocentrische theorie bedacht..
De verantwoordelijke kracht is de aantrekkingskracht. Deze kracht hangt rechtstreeks af van de massa van de ster en de planeet in kwestie en is omgekeerd evenredig met het kwadraat van de afstand die hen scheidt..
Het probleem is niet zo eenvoudig, omdat in een zonnestelsel alle elementen op deze manier op elkaar inwerken, waardoor de materie complexer wordt. Bovendien zijn het geen deeltjes, aangezien sterren en planeten meetbare afmetingen hebben..
Om deze reden is het centrale punt van de baan of het circuit dat door de planeten wordt afgelegd, niet precies gecentreerd rond de ster, maar op een punt dat bekend staat als het zwaartepunt van het zonneplanetenstelsel..
De resulterende baan is elliptisch. De volgende afbeelding laat het zien, waarbij de aarde en de zon als voorbeeld worden genomen:
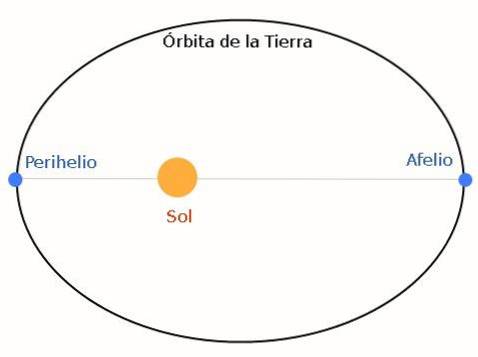
Het aphelium is de verste positie op aarde van de zon, terwijl het perihelium het dichtstbijzijnde punt is. De ellips kan min of meer afgeplat zijn, afhankelijk van de kenmerken van het ster-planetenstelsel..
De aphelium- en periheliumwaarden variëren jaarlijks, omdat de andere planeten verstoringen veroorzaken. Voor andere planeten worden deze posities respectievelijk apoaster en periaster genoemd..
De grootte van de lineaire snelheid van een planeet is niet constant
Kepler ontdekte dat wanneer een planeet in een baan om de zon draait, deze tijdens zijn beweging in gelijke tijden gelijke gebieden opneemt. Figuur 2 geeft grafisch de betekenis hiervan weer:
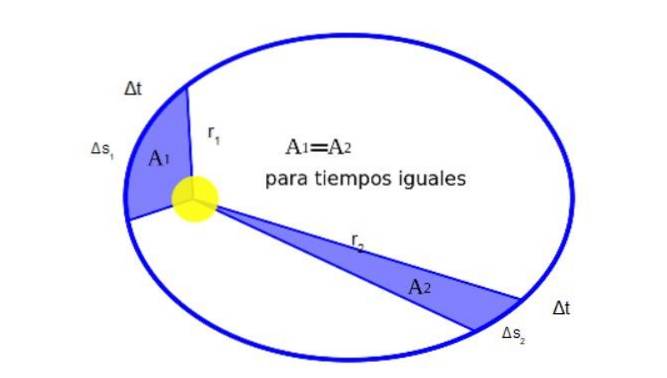
Wiskundig gezien is het feit dat A1 gelijk zijn aan Atwee wordt als volgt uitgedrukt:

De afgelegde bogen Δs zijn klein, zodat elk gebied dat van een driehoek kan benaderen:
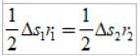
Omdat Δs =vΔt, waarbij v de lineaire snelheid van de planeet op een bepaald punt is, door deze te vervangen hebben we:
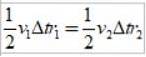
En aangezien het tijdsinterval Δt hetzelfde is, krijgen we:
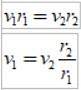
Zoals rtwee > r1, dan v1 > vtwee, met andere woorden, de lineaire snelheid van een planeet is niet constant. In feite gaat de aarde sneller als ze zich in het perihelium bevindt dan wanneer ze zich in een aphelium bevindt..
Daarom is de lineaire snelheid van de aarde of van een willekeurige planeet rond de zon niet een grootte die dient om de beweging van die planeet te karakteriseren..
Areolaire snelheid
De tweede wet van Kepler suggereert een nieuwe magnitude genaamd areolaire snelheid. Het wordt gedefinieerd als het geveegde oppervlak per tijdseenheid en is constant. Om het te berekenen, wordt de volgende afbeelding gebruikt:
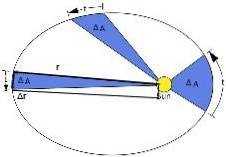
Een klein gebied dat door de aarde wordt geveegd, wordt gekozen tijdens het maken van zijn elliptische circuit, dat we zullen aanduiden als ΔA. De tijd die hiervoor nodig is, is Δt.
Figuur 3 toont de positievector van de aarde ten opzichte van de zon, aangegeven met r. Wanneer de aarde beweegt, ervaart ze een verplaatsing Δr.
Dit gebied komt overeen met de helft van het gebied van de rechthoek weergegeven in figuur 3:
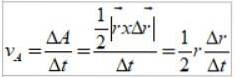
Het quotiënt Δr / Δt is precies de lineaire snelheid van de aarde, dus de areolaire snelheid is als:
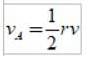
De eenheden van vNAAR in het internationale systeem zijn ze:
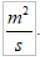
Merk op dat hoewel r en v variëren, het product constant blijft. Dit maakt de areolaire snelheid een zeer geschikte grootte om de beweging van een planeet rond zijn ster te karakteriseren..
Het product van r en v is de grootte van het impulsmoment L, zodat de areolaire snelheid kan worden uitgedrukt als:
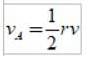
Berekenen van lineaire snelheid en areolaire snelheid
Met het volgende voorbeeld laten we zien hoe de areolaire snelheid berekend kan worden als enkele parameters van planetaire beweging bekend zijn:
Oefening
Volgens de wetten van Kepler beweegt een exo-planeet om zijn zon in een elliptische baan. Als het zich in de periaster bevindt, is de straalvector r1 = 4 107 km, en als het in apoastro is, is het rtwee = 15 107 km. De lineaire snelheid op zijn periaster is v1 = 1000 km / s.
Berekenen:
A) De grootte van de snelheid bij de apoastro.
B) De areolaire snelheid van de exo-planeet.
C) De lengte van de semi-hoofdas van de ellips.
Antwoord op)
De vergelijking wordt gebruikt:
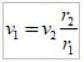
waarin numerieke waarden worden vervangen.
Elke term wordt als volgt geïdentificeerd:
v1 = snelheid in apoastro; vtwee = snelheid in de periaster; r1= afstand vanaf apoastro,
rtwee= afstand tot de periaster.
Met deze waarden krijg je:

Antwoord B)
De te gebruiken vergelijking is
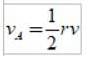
waarin het waardenpaar r en v van de periaster of van de apoaster kan worden vervangen, aangezien vNAAR is een constante van de planeet:

Antwoord C)
De lengte van de semi-hoofdas van de ellips is het semisum van de apoaster en de periaster:
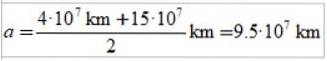
Bibliografie
- Serway, R., Jewett, J. (2008). Physics for Science and Engineering. Deel 1. Mexico. Cengage Learning Editors. 367-372.
- Stern, D. (2005). Kepler's drie wetten van planetaire beweging. Opgehaald van pwg.gsfc.nasa.gov
- Opmerking: de voorgestelde oefening is overgenomen en gewijzigd van de volgende tekst in een McGrawHill-boek. Helaas is het een geïsoleerd hoofdstuk in pdf-formaat, zonder de titel of de auteur: mheducation.es/bcv/guide/capitulo/844817027X.pdf

Niemand heeft nog op dit artikel gereageerd.