De relatieve snelheid van een object is er een die wordt gemeten ten opzichte van een bepaalde waarnemer, aangezien een andere waarnemer een andere meting kan verkrijgen. Snelheid hangt altijd af van de waarnemer die het meet.
Daarom is de snelheid van een object gemeten door een bepaalde persoon de relatieve snelheid ten opzichte van het object. Een andere waarnemer kan een andere waarde voor de snelheid verkrijgen, zelfs als het hetzelfde object is.
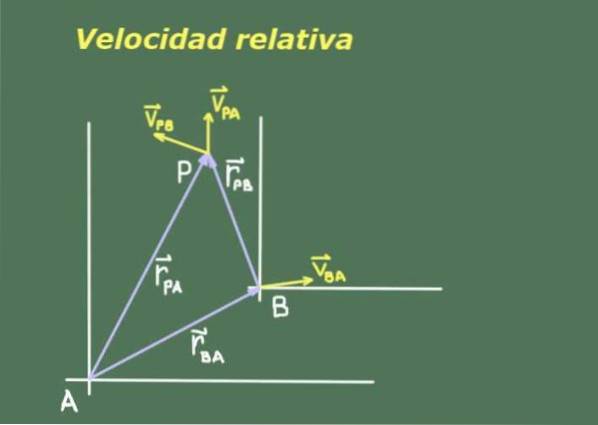
Aangezien twee waarnemers A en B die ten opzichte van elkaar bewegen, verschillende metingen kunnen hebben van een derde bewegend object P, is het noodzakelijk om een verband te zoeken tussen de posities en snelheden van P gezien door A en B.
Figuur 1 toont twee waarnemers A en B met hun respectievelijke referentiesystemen, van waaruit ze de positie en snelheid van het object P meten.
Elke waarnemer A en B meet de positie en snelheid van het object P op een bepaald tijdstip t. In de klassieke (of Galileïsche) relativiteitstheorie is de tijd voor waarnemer A dezelfde als voor waarnemer B, ongeacht hun relatieve snelheden.
Dit artikel gaat over de klassieke relativiteitstheorie die geldig en toepasbaar is in de meeste alledaagse situaties waarin objecten veel lagere snelheden hebben dan die van licht..
We duiden de positie van waarnemer B ten opzichte van A aan als rBA. Omdat positie een vectorgrootheid is, gebruiken we vet om dit aan te duiden. De positie van het object P ten opzichte van A wordt aangeduid als rVADER en dat van hetzelfde object P met betrekking tot B rPB.
Artikel index
Er is een vectorrelatie tussen deze drie posities die kan worden afgeleid uit de weergave van figuur 1:
rVADER rPB + rBA
Als de afgeleide van de vorige uitdrukking wordt genomen met betrekking tot tijd t we zullen de relatie verkrijgen tussen de relatieve snelheden van elke waarnemer:
V.VADER V.PB + V.BA
In de vorige uitdrukking hebben we de relatieve snelheid van P ten opzichte van A als functie van de relatieve snelheid van P ten opzichte van B en de relatieve snelheid van B ten opzichte van A.
Evenzo kan de relatieve snelheid van P ten opzichte van B worden geschreven als een functie van de relatieve snelheid van P ten opzichte van A en de relatieve snelheid van A ten opzichte van B..
V.PB V.VADER + V.AB
Opgemerkt moet worden dat de relatieve snelheid van A ten opzichte van B gelijk is aan en tegengesteld aan die van B ten opzichte van A:
V.AB -V.BA
Een auto rijdt op een rechte weg, die van west naar oost gaat, met een snelheid van 80 km / u terwijl in de tegenovergestelde richting (en vanaf de andere rijstrook) een motorfiets komt met een snelheid van 100 km / u.
Een jongen rijdt op de achterbank van de auto die de relatieve snelheid wil weten van een motorfiets die hem nadert. Om het antwoord te achterhalen, past het kind de relaties toe die hij zojuist in de vorige paragraaf heeft gelezen, waarbij het elk coördinatensysteem als volgt identificeert:
-A is het coördinatensysteem van een waarnemer op de weg en ten opzichte daarvan zijn de snelheden van elk voertuig gemeten.
-B is de auto en P is de motorfiets.
Wil je de snelheid van motor P ten opzichte van auto B berekenen, dan wordt de volgende relatie gehanteerd:
V.PB V.VADER + V.ABV.VADER - V.BA
Als we de west-oost richting positief nemen, hebben we:
V.PB= (-100 km / u - 80 km / u) ik = -180 km / u ik
Dit resultaat wordt als volgt geïnterpreteerd: de motorfiets beweegt ten opzichte van de auto met een snelheid van 180 km / u en richting -ik, dat wil zeggen, van oost naar west.
De motor en de auto zijn elkaar gekruist en hebben hun rijstrook gevolgd. Het kind op de achterbank van de auto ziet de motor wegrijden en wil nu weten hoe snel hij van hem af beweegt, ervan uitgaande dat zowel de motor als de auto dezelfde snelheid aanhouden als voor het oversteken..
Om het antwoord te weten, past het kind dezelfde relatie toe die eerder werd gebruikt:
V.PB V.VADER + V.ABV. VADER - V.BA
V.PB= -100 km / u ik - 80 km / u ik = -180 km / u ik
En nu beweegt de motorfiets zich van de auto af met dezelfde relatieve snelheid waarmee hij naderde voordat ze overstaken..
Dezelfde motorfiets uit deel 2 wordt geretourneerd met dezelfde snelheid van 100 km / u maar verandert van richting. Dat wil zeggen, de auto (die doorgaat met een snelheid van 80 km / u) en de motorfiets rijden beide in een positieve oost-west richting..
Op een gegeven moment passeert de motorfiets de auto en het kind op de achterbank van de auto wil de relatieve snelheid van de motorfiets ten opzichte van hem weten wanneer hij deze voorbij ziet rijden..
Om het antwoord te krijgen, past het kind de relaties van relatieve beweging opnieuw toe:
V.PB V.VADER + V.ABV.VADER - V.BA
V.PB= +100 km / u ik - 80 km / u ik = 20 km / u ik
Het kind vanaf de achterbank kijkt met een snelheid van 20 km / u naar de motorfiets die de auto inhaal.
Een motorboot steekt een rivier over die 600 m breed is en van noord naar zuid stroomt. De snelheid van de rivier is 3 m / s. De snelheid van de boot ten opzichte van het water van de rivier is 4 m / s naar het oosten.
(i) Zoek de snelheid van de boot ten opzichte van de oever van de rivier.
(ii) Geef de snelheid en richting van de boot ten opzichte van het land aan.
(iii) Bereken de crossover-tijd.
(iv) Hoe ver naar het zuiden is het verplaatst vanaf het startpunt.
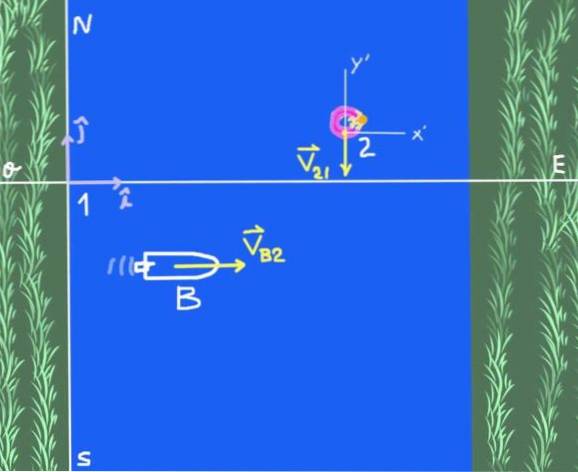
Er zijn twee referentiesystemen: het solidaire referentiesysteem op de rivieroever dat we 1 zullen noemen en het referentiesysteem 2, een waarnemer die op het rivierwater drijft. Het onderwerp van studie is boot B.
De snelheid van de boot ten opzichte van de rivier wordt als volgt in vectorvorm geschreven:
V.B2 = 4 ik Mevrouw
De snelheid van waarnemer 2 (vlot op de rivier) ten opzichte van waarnemer 1 (op het land):
V.eenentwintig = -3 j Mevrouw
U wilt de snelheid van de boot ten opzichte van het land vinden V.B1.
V.B1 = VB2 + V.eenentwintig
V.B1 (4 ik - 3 j) Mevrouw
De snelheid van de boot is de modulus van de vorige snelheid:
V.B1= (42 + (-3) 2) ½ = 5 m / s
En het adres zal zijn:
θ = arctan (-¾) = -36,87º
De oversteektijd van de boot is het quotiënt tussen de breedte van de rivier en de x-component van de snelheid van de boot ten opzichte van het land.
t = (600m) / (4 m / s) = 150 s
Om de drift te berekenen die de boot naar het zuiden had, wordt de y-component van de bootsnelheid ten opzichte van land vermenigvuldigd met de oversteektijd:
d = -3 j m / s * 150 s = -450 j m
De verplaatsing naar het zuiden tov het startpunt is 450m.
Niemand heeft nog op dit artikel gereageerd.