
Mesh-analyseconcepten, methoden, voorbeelden
De mesh-analyse is een techniek die wordt gebruikt om platte elektrische circuits op te lossen. Deze procedure kan ook in de literatuur voorkomen onder de methodenamen van de circuit stromen of methode van maasstromen (of lus).
De basis van deze en andere analysemethoden voor elektrische circuits ligt in de wetten van Kirchhoff en de wet van Ohm. De wetten van Kirchhoff zijn op hun beurt uitdrukkingen van twee zeer belangrijke principes van behoud in de natuurkunde voor geïsoleerde systemen: zowel de elektrische lading als de energie blijven behouden..

Enerzijds is de elektrische lading gerelateerd aan de stroom, wat de lading in beweging is, terwijl in een circuit de energie is gekoppeld aan de spanning, die de agent is die verantwoordelijk is voor het uitvoeren van het werk dat nodig is om de lading binnen te houden beweging..
Deze wetten, toegepast op een vlak circuit, genereren een reeks gelijktijdige vergelijkingen die moeten worden opgelost om de stroom- of spanningswaarden te verkrijgen..
Het stelsel van vergelijkingen kan worden opgelost met bekende analytische technieken, zoals regel van cramer, dat vereist de berekening van determinanten om de oplossing van het systeem te verkrijgen.
Afhankelijk van het aantal vergelijkingen worden ze opgelost met behulp van een wetenschappelijke rekenmachine of wiskundige software. Op het net zijn er ook veel opties beschikbaar.
Artikel index
- 1 Belangrijke termen
- 2 methoden
- 2.1 - Stappen om mesh-analyse toe te passen
- 3 Opgeloste oefeningen
- 3.1 - Voorbeeld 1
- 3.2 - Voorbeeld 2
- 4 referenties
Belangrijke termen
Voordat we uitleggen hoe het werkt, beginnen we met het definiëren van deze termen:
Afdeling: sectie met een circuitelement.
Knooppunt: punt dat twee of meer takken verbindt.
Lint: is elk gesloten deel van een circuit, beginnend en eindigend bij hetzelfde knooppunt.
Mesh: loop die geen andere loop bevat binnen (essentieel mesh.
Methoden
Mesh-analyse is een algemene methode die wordt gebruikt om circuits op te lossen waarvan de elementen in serie, parallel of op een gemengde manier zijn verbonden, dat wil zeggen wanneer het type verbinding niet duidelijk wordt onderscheiden. Het circuit moet vlak zijn, of het moet in ieder geval mogelijk zijn om het als zodanig opnieuw te tekenen.
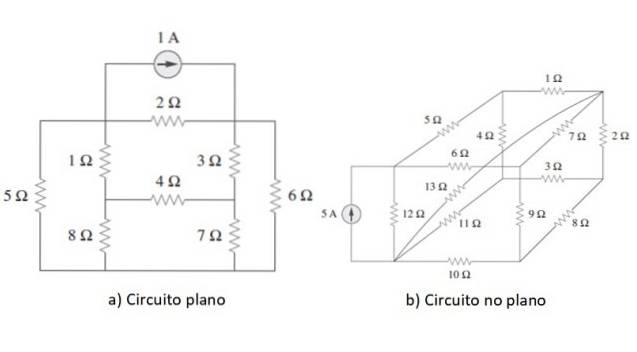
Een voorbeeld van elk type circuit wordt getoond in de bovenstaande afbeelding. Zodra het punt is opgehelderd, zullen we om te beginnen de methode toepassen op een eenvoudig circuit als voorbeeld in de volgende sectie, maar eerst zullen we kort de wetten van Ohm en Kirchhoff bespreken..
De wet van Ohm: worden V. de spanning, R weerstand e ik de stroom van het ohmse weerstandselement, waarin de spanning en stroom recht evenredig zijn, waarbij de weerstand de evenredigheidsconstante is:
V = I.R
Kirchhoff's wet van spanning (LKV): In elk gesloten pad dat in slechts één richting wordt afgelegd, is de algebraïsche som van de spanningen nul. Dit omvat spanningen als gevolg van bronnen, weerstanden, inductoren of condensatoren: ∑ E = ∑ Rik. ik
De huidige wet van Kirchhoff (LKC): op elk knooppunt is de algebraïsche som van de stromen nul, rekening houdend met het feit dat de inkomende stromen het ene teken krijgen en de stromen die een andere verlaten. Op deze manier: ∑ I = 0.
Met de mesh current-methode is het niet nodig om de huidige wet van Kirchhoff toe te passen, waardoor er minder vergelijkingen zijn om op te lossen.
- Stappen om mesh-analyse toe te passen
We beginnen met het uitleggen van de methode voor een circuit met 2 mazen. De procedure kan dan worden uitgebreid voor grotere circuits.
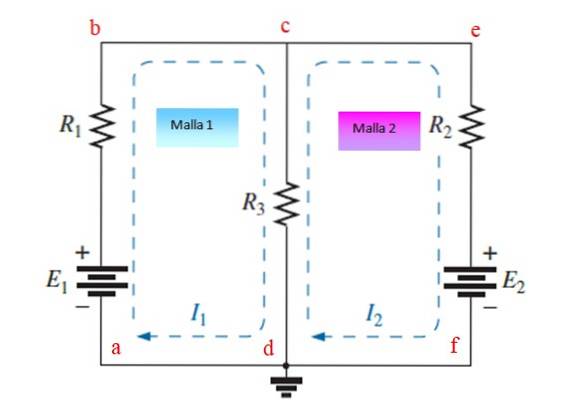
Stap 1
Wijs onafhankelijke stromen toe aan elke mesh en teken deze, in dit voorbeeld zijn ze dat ik1 en iktwee. Ze kunnen met de klok mee of tegen de klok in worden getekend.
Stap 2
Pas de wet van spanningen van Kirchhoff (LTK) en de wet van Ohm toe op elke mesh. Potentiële dalingen krijgen een teken (-) terwijl stijgingen een teken (+) krijgen.
Mesh abcda
Beginnend bij punt a en in de richting van de stroom, vinden we een mogelijke stijging van batterij E1 (+), dan een daling van R1 (-) en dan nog een druppel in R3 .
Tegelijkertijd is de weerstand R3 wordt ook doorkruist door huidige Itwee, maar in de tegenovergestelde richting vertegenwoordigt het daarom een stijging (+). De eerste vergelijking ziet er als volgt uit:
EN1-R1.ik1 -R3.ik1 + R3.iktwee = 0
Vervolgens wordt er rekening mee gehouden en worden de termen opnieuw gegroepeerd:
- (R.1+R3) Ik1 +R3iktwee = -E1 (Vergelijking 1)
Cefdc mesh
Beginnend vanaf het punt en en in de richting van de stroom wordt een potentiële daling gevonden in Rtwee (-), nog een drop-in ENtwee, omdat de stroom binnenkomt via de + pool van de batterij en uiteindelijk weer naar binnen valt R3 (-), Tegelijkertijd de huidige ik1 doorkruist R3 in tegengestelde richting (+).
De tweede vergelijking, met de aangegeven tekens, ziet er als volgt uit:
- Rtwee iktwee - ENtwee -R3 iktwee +R3 ik1= 0
R3ik1 - (R.twee +R3) iktwee = Etwee (Vergelijking 2)
Merk op dat er twee vergelijkingen zijn met de twee onbekenden I1 en iktwee.
Stap 3
Het aldus gevormde stelsel van vergelijkingen wordt dan opgelost.
Opgeloste oefeningen
Om te beginnen is het belangrijk om het volgende te overwegen:
-Lusstromen of maasstromen kunnen een willekeurig adres worden toegewezen.
-Aan elk essentieel mesh - of "venster" - dat het circuit heeft, moet een stroom worden toegewezen.
-Maasstromen worden aangeduid met een hoofdletter om ze te onderscheiden van stromen die door takken circuleren, hoewel in sommige gevallen de stroom die door een tak circuleert dezelfde kan zijn als die van mesh.
- voorbeeld 1
Zoek de stromen die door elke weerstand in het circuit van figuur 3 vloeien, als de elementen de volgende waarden hebben:
R1 = 20 Ω; Rtwee = 30 Ω; R3 = 10 Ω; EN1 = 12 V; ENtwee = 18 V
Oplossing
Ten eerste is het noodzakelijk om de maasstromen I toe te wijzen1 en iktwee en neem het stelsel van vergelijkingen zoals afgeleid in de vorige sectie, en vervang dan de waarden die in de verklaring worden gegeven:
- (R.1+R3) Ik1 +R3iktwee = -E1 (Vergelijking 1)
R3ik1 - (R.twee +R3) iktwee = Etwee (Vergelijking 2)
-
-(20 + 30) ik1 + 10Itwee = -12
10I1 - (30 +10) Itwee = 18
--
-vijftigik1 + 10Itwee = -12
10I1 - 40 iktwee = 18
Omdat het een 2 x 2 stelsel van vergelijkingen is, kan het gemakkelijk worden opgelost door reductie, waarbij de tweede vergelijking met 5 wordt vermenigvuldigd om het onbekende te elimineren ik1
-vijftigik1 + 10 iktwee = -12
50I1 - 200 iktwee = 90
-
-190 Itwee= 78
iktwee = - 78/180 A = - 0,41 A
Meteen wordt de stroom gewist ik1 van een van de originele vergelijkingen:
ik1 = (18 + 40 iktwee) / 10 = (18 + 40 x (-0,41)) / 10 = 0,16 A
Het minteken in de stroom iktwee betekent dat de stroom in mesh 2 in tegengestelde richting circuleert.
De stromen in elke weerstand zijn als volgt:
Voor het verzet R1 de stroom circuleert ik1 = 0,16 A in de zin getrokken door weerstand Rtwee de stroom circuleert iktwee = 0,41 A in de tegenovergestelde richting van degene die wordt getrokken, en door de weerstand R3 circuleren ik3 = 0,16- (-0,41) A = 0,57 A naar beneden.
Systeemoplossing volgens de methode van Cramer
In matrixvorm kan het systeem als volgt worden opgelost:
Stap 1: Bereken Δ

Stap 2: Bereken Δ1
De eerste kolom wordt vervangen door de onafhankelijke termen van het stelsel vergelijkingen, waarbij de volgorde wordt gehandhaafd waarin het systeem oorspronkelijk werd voorgesteld:

Stap 3: Bereken I.1
ik1 = Δ1/ Δ = 300/1900 = 0,16 A
Stap 4: Bereken Δtwee

iktwee = Δtwee/ Δ = -780/1900 = -0,41 EEN
- Voorbeeld 2
Bepaal de stroom en spanningen door elke weerstand in het volgende circuit met behulp van de maasstromen-methode:

Oplossing
De drie maasstromen worden, zoals weergegeven in de volgende afbeelding, in willekeurige richtingen getekend. Nu worden de mazen doorkruist vanaf elk punt:
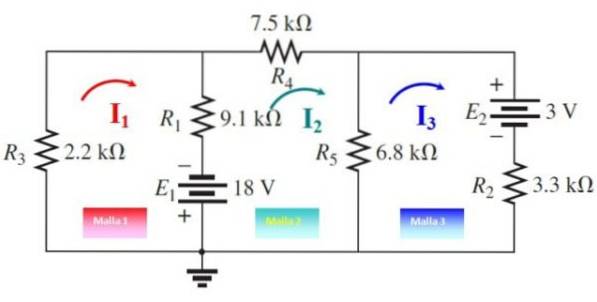
Mesh 1
-9100.I1+18-2200.I1+9100.Itwee= 0
-11300 I1 + 9100.Itwee = -18
Mesh 2
-(7500 + 6800 + 9100) I.twee + 9100.I1+6800.I3-18 = 0
9100.I1 - 23400.Itwee + 6800.I3 = 18
Mesh 3
-(6800 + 3300) I3 + 6800.Itwee - 3 = 0
6800.Itwee - 10100.I3 = 3
Stelsel van vergelijkingen
-11300 I1 + 9100.Itwee + 0.I3= -18
9100.I1 - 23400.Itwee + 6800.I3 = 18
0.I1 + 6800.Itwee - 10100.I3 = 3
Hoewel de cijfers groot zijn, kan het snel worden opgelost met behulp van een wetenschappelijke rekenmachine. Onthoud dat de vergelijkingen moeten worden geordend en nullen moeten worden toegevoegd op de plaatsen waar het onbekende niet verschijnt, zoals het hier voorkomt.
De maasstromen zijn:
ik1 = 0,0012 A; iktwee = -0,00048 A; ik3 = -0.00062 EEN
Stromingen iktwee en ik3 circuleren in de tegenovergestelde richting van de richting die in de figuur wordt getoond, aangezien ze negatief bleken te zijn.
Tabel met stromen en spanningen in elke weerstand
| Weerstand (Ω) | Stroom (ampère) | Spanning = I.R (Volt) |
|---|---|---|
| 9100 | ik1 -iktwee = 0,0012 - (- 0,00048) = 0,00168 | 15.3 |
| 3300 | 0.00062 | 2.05 |
| 2200 | 0,0012 | 2,64 |
| 7500 | 0.00048 | 3,60 |
| 6800 | iktwee -ik3= -0.00048 - (- 0.00062) = 0.00014 | 0,95 |
De regeloplossing van Cramer
Omdat het grote getallen zijn, is het handig om wetenschappelijke notatie te gebruiken om er direct mee te werken.
Berekening van I1
De gekleurde pijlen in de 3 x 3 determinant geven aan hoe de numerieke waarden kunnen worden gevonden door de aangegeven waarden te vermenigvuldigen. Laten we beginnen met die van de eerste haak in de determinant Δ:
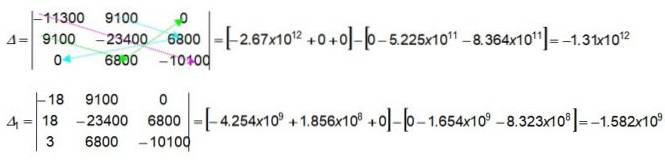
(-11300) x (-23400) x (-10100) = -2,67 x 1012
9100 x 0 x 0 = 0
9100 x 6800 x 0 = 0
Meteen krijgen we het tweede haakje in dezelfde determinant, die van links naar rechts wordt gewerkt (voor dit haakje zijn de gekleurde pijlen niet getekend in de figuur). We nodigen de lezer uit om het te verifiëren:
0 x (-23400) x 0 = 0
9100 x 9100 x (-10100) = -8,364 x 10elf
6800 x 6800 x (-11300) = -5,225 x 10elf
Evenzo kan de lezer ook de waarden voor de determinant controleren Δ1.
Belangrijk: tussen beide haakjes staat altijd een negatief teken.
Eindelijk krijg je de stroom ik1 door ik1 = Δ1 / Δ
ik1 = -1,582 x 109/ - 1,31 x 1012 = 0,0012 A
Berekening van Itwee
De procedure kan worden herhaald om te berekenen iktwee, in dit geval om de determinant Δ te berekenentwee de tweede kolom van de determinant Δ wordt vervangen door de kolom met de onafhankelijke termen en de waarde ervan wordt gevonden volgens de beschreven procedure.
Omdat het echter omslachtig is vanwege de grote getallen, vooral als u geen wetenschappelijke rekenmachine heeft, is het het gemakkelijkst om de waarde van ik1 al berekend, in de volgende vergelijking en duidelijk:
-11300 I1 + 9100.Itwee + 0.I3= -18 → 9100 Itwee= -18 + 11300 ik1 → iktwee = -0.00048 EEN
Berekening van I3
Een keer met de waarden van ik1 en iktwee in de hand, dat van ik3 rechtstreeks gevonden door vervanging.
Referenties
- Alexander, C. 2006. Grondbeginselen van elektrische schakelingen. 3e. Editie. Mc Graw Hill.
- Boylestad, R. 2011. Inleiding tot circuitanalyse. 2da. Editie. Pearson.
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 5. Elektrische interactie. Bewerkt door Douglas Figueroa (USB).
- García, L. 2014. Elektromagnetisme. 2e. Editie. Industriële Universiteit van Santander.
- Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. Ed. Deel 2.



Niemand heeft nog op dit artikel gereageerd.