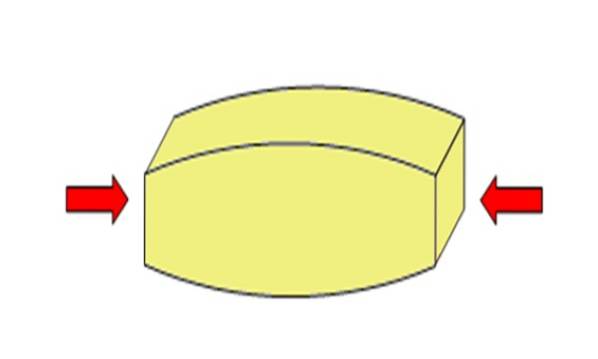
De compressie of drukspanning is de kracht per oppervlakte-eenheid waarvan het resultaat is dat een voorwerp wordt geduwd, samengedrukt of gecomprimeerd, waardoor het wordt verkort. Wiskundig is het:
E = F / A
Hier EN staat voor inspanning, F. de grootte van de kracht en NAAR het gebied waarop het werkt, waarbij de eenheid in het SI International System de newton / m istwee of pascal (Pa). Drukspanning is een normale inspanning, omdat de kracht die het produceert loodrecht staat op het gebied waarop het wordt uitgeoefend.
Een dergelijke inspanning kan het object samendrukken of, integendeel, spannen en uitrekken, zoals het wordt toegepast. In het geval van drukspanning worden de krachten in de tegenovergestelde richting uitgeoefend om het effect van het samenknijpen en inkorten van het object uit te oefenen.
Zodra de krachten wegvallen, keren veel materialen terug naar hun oorspronkelijke afmetingen. Deze eigenschap is bekend onder de naam elasticiteit. Maar terwijl dat gebeurt, is de vervorming van de elastische eenheid die wordt opgelopen door een materiaal dat aan spanning wordt blootgesteld:
Strain = (Final Size - Initial Size) / Initial Size
De rek kan lineair, oppervlakkig of volumetrisch zijn, hoewel rek geen eenheid is. De informatie die het geeft is echter erg belangrijk, aangezien het niet hetzelfde is om een staaf van 10 m lang met 1 cm te vervormen, om een andere staaf van 1 m lang met 1 cm te vervormen..
In een elastisch materiaal zijn vervorming en spanning proportioneel en voldoen ze aan de wet van Hooke:
Inspanning ∝ Vervorming van het apparaat
Artikel index
De drukspanning zorgt ervoor dat de deeltjes van het materiaal steeds dichterbij komen, waardoor ze kleiner worden. Afhankelijk van de richting waarin de inspanning wordt uitgeoefend, zal een deel van de afmetingen worden verkort of verkleind.
Laten we beginnen met een dunne staaf van oorspronkelijke lengte aan te nemen L., tot welke normale spanning van grootte EN. Als de spanning drukkend is, ervaart de staaf een vermindering van de lengte, aangeduid met δ. Als het spanning is, wordt de balk langer.
Het materiaal waaruit het element is gemaakt, is natuurlijk doorslaggevend voor het vermogen om stress te weerstaan..
Deze elastische eigenschappen van het materiaal zijn opgenomen in de bovengenoemde evenredigheidsconstante. Is genaamd elasticiteitsmodulus of Young's modulus en wordt aangeduid als Y. Elk materiaal heeft een elasticiteitsmodulus, die experimenteel wordt bepaald door laboratoriumtests.
Met dit in gedachten, de moeite EN Het wordt als volgt in wiskundige vorm uitgedrukt:
Inspanning ∝ Vervorming van het apparaat
Tenslotte, om deze voorwaarde als een vergelijking vast te stellen, is een evenredigheidsconstante vereist om het symbool van evenredigheid ∝ te vervangen door gelijkheid, als volgt:
Spanning = evenredigheidsconstante x eenheidsrek
E = Y. (δ / L)
Het quotiënt (δ / L) is de stam, aangeduid als ε en met δ Uiteindelijke lengte - initiële lengte. Op deze manier de moeite EN lijkt op:
E = Y. ε
Omdat stam dimensieloos is, zijn de eenheden van Y zijn dezelfde als die van EN: N / mtwee o Pa in het SI-systeem, ponden / intwee of psi in het Britse systeem, evenals andere combinaties van kracht en oppervlakte, zoals kg / cmtwee.
Y-waarden worden experimenteel bepaald in het laboratorium, onder gecontroleerde omstandigheden. Vervolgens de elasticiteitsmodulus voor materialen die veel worden gebruikt in de constructie en ook die van botten:
tafel 1
| Materiaal | Elasticiteitsmodulus Y (Pa) x 109 |
|---|---|
| Staal | 200 |
| Ijzer | 100 |
| Messing | 100 |
| Bronzen | 90 |
| Aluminium | 70 |
| Marmeren | vijftig |
| Graniet | Vier vijf |
| Beton | twintig |
| Bot | vijftien |
| Pinewood | 10 |
Drukkrachten werken op verschillende constructies; Ze zijn onderhevig aan de werking van krachten zoals het gewicht van elk van de elementen waaruit ze bestaan, evenals krachten van externe factoren: wind, sneeuw, andere constructies en meer..
Het is gebruikelijk dat de meeste constructies zijn ontworpen om alle soorten spanningen te weerstaan zonder te vervormen. Daarom moet rekening worden gehouden met de compressiespanning om te voorkomen dat het onderdeel of object zijn vorm verliest..
Ook de botten van het skelet zijn structuren die aan verschillende spanningen worden blootgesteld. Hoewel de botten hiertegen resistent zijn, ontstaan bij per ongeluk de elastische limiet scheuren en breuken.
Bouwkolommen en pijlers moeten zo worden gemaakt dat ze bestand zijn tegen compressie, anders hebben ze de neiging om te buigen. Dit staat bekend als zijwaarts buigen of knik.
De kolommen (zie figuur 1) zijn elementen waarvan de lengte aanzienlijk groter is in vergelijking met hun dwarsdoorsnede..
Een cilindrisch element is een kolom waarvan de lengte gelijk is aan of groter is dan tien keer de diameter van de doorsnede. Maar als de doorsnede niet constant is, wordt de kleinere diameter genomen om het element als een kolom te classificeren.
Wanneer mensen plaatsnemen op meubels zoals stoelen en banken, of er voorwerpen bovenop leggen, worden de benen blootgesteld aan drukspanningen die de neiging hebben om hun hoogte te verkleinen..
Meubels zijn meestal gemaakt om redelijk goed tegen het gewicht te kunnen en keren na verwijdering terug naar hun natuurlijke staat. Maar als er zwaar gewicht op kwetsbare stoelen of banken wordt geplaatst, maken de benen plaats voor compressie en breken ze..
Er is een staaf die oorspronkelijk 12 m lang is, waaraan hij wordt onderworpen aan een drukspanning zodat de vervorming van de eenheid -0,0004 is. Wat is de nieuwe lengte van de staaf?
Uitgaande van de bovenstaande vergelijking:
ε = (δ / L) = - 0,0004
Ja L.F. is de uiteindelijke lengte en L.of de aanvankelijke lengte, sinds δ = LF. - L.of jij hebt:
(L.F. - L.of) / Lof = -0.0004
Daarom: L.F. - L.of = -0,0004 x 12 m = -0,0048 m. En tenslotte:
L.F. = (12 - 0,0048) m = 11,9952 m.
Een massief stalen staaf, cilindrisch van vorm, is 6 m lang en 8 cm in diameter. Als de staaf wordt samengedrukt door een belasting van 90.000 kg, zoek dan:
a) De grootte van de drukspanning in megapascal (MPa)
b) Met hoeveel is de lengte van de staaf afgenomen?
Eerst vinden we het gebied A van de doorsnede van de staaf, dat afhangt van de diameter D, resulterend in:
A = π. Dtwee / 4 = π. (0,08 m)twee / 4 = 5,03 x 10-3 mtwee
De kracht wordt onmiddellijk gevonden, door F = m.g = 90.000 kg x 9,8 m / stwee= 882.000 N.
Ten slotte wordt de gemiddelde inspanning als volgt berekend:
E = F / A = 882.000 N / 5,03 x 10-3 mtwee = 1,75 x 108 Pa = 175 MPa
Nu wordt de vergelijking voor spanning gebruikt, wetende dat het materiaal een elastische respons heeft:
E = Y. (δ / L)
De Young's modulus van staal is te vinden in Tabel 1:
δ = E.L / Y = 6 m x 1,75 x 108 Pa / 200 x 10 9 Pa = 5,25 x 10 -3 m = 5,25 mm.
Niemand heeft nog op dit artikel gereageerd.