
Gratis lichaamsdiagram hoe het te doen, voorbeelden, oefening
EEN Vrijlichaam diagram, geïsoleerd lichaamsdiagram of krachtdiagram, is een diagram waarin de krachten die op een lichaam inwerken, worden weergegeven door pijlen.
Zorg ervoor dat u het in het diagram opneemt alle de krachten die op het object inwerken, en aangezien het een vectorgrootheid is, is de pijl verantwoordelijk voor het aangeven van de richting en de zin, terwijl de lengte een idee geeft van de modulus of intensiteit.
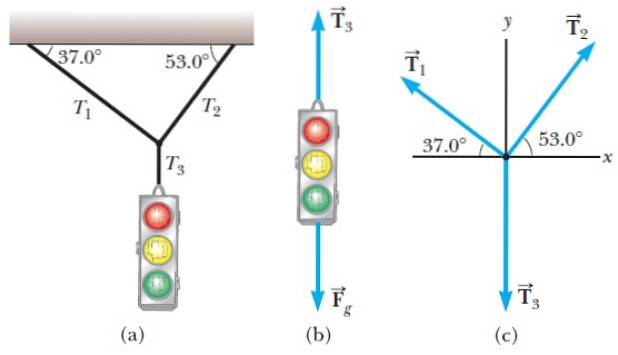
In figuur 1 hebben we een voorbeeld van een gratis lichaamsdiagram dat we gaan analyseren.
De situatie is als volgt: een stoplicht hangt stil aan enkele kabels (figuur 1a). Twee krachten werken erop, de ene wordt uitgeoefend door de aarde, wat het gewicht is. In het diagram wordt het aangeduid als F.g en werkt verticaal naar beneden.
De andere kracht is de spanning in de verticale snaar, genaamd T3 en dat gaat in verticale richting naar boven, waarbij het verkeerslicht wordt vastgehouden en niet op de grond valt.
Als een probleem meer dan één object heeft, moet voor elk afzonderlijk een diagram worden getekend..
De knoop tussen de hellende touwen en het touw dat het verkeerslicht vasthoudt, wordt beschouwd als een puntobject en het vrije-lichaamdiagram is in figuur 1c. Merk op dat voor de knoop, de spanning T3 is naar beneden gericht.
Het is belangrijk op te merken dat de krachten die door het object op andere lichamen worden uitgeoefend, niet in het free-body-diagram moeten voorkomen, maar alleen degenen die ernaar handelen.
Artikel index
- 1 Voorbeelden van een vrijlichaamdiagram
- 1.1 Een persoon die een kofferbak of container trekt
- 1.2 Een blok dat van een hellend vlak naar beneden glijdt
- 1.3 Atwood's machine
- 2 Oefening opgelost
- 2.1 Oplossing
- 3 referenties
Voorbeelden van free-body diagrammen
Het vrije-lichaamsdiagram maakt de toepassing van de wetten van Newton mogelijk en bepaalt daarmee de bewegingstoestand of de rest van het object waarop de krachten werken. In het geval van het getoonde stoplicht kunnen we de waarde bepalen van de spanningen in de kabels die het stoplicht vasthouden, wetende wat het gewicht hiervan is.
Als deze gegevens eenmaal bekend zijn, worden geschikte kabels geselecteerd om het verkeerslicht op te hangen en die hun functie vervullen zonder te bezwijken.
Free-body-diagrammen worden gebruikt om verschillende alledaagse situaties te beschrijven, zoals deze:
Een persoon die een koffer of container trekt
Het is heel gebruikelijk dat mensen zware voorwerpen moeten dragen, zoals de container in de figuur. Om dit te doen, moeten ze een kracht uitoefenen F. over de container, die in dit voorbeeld horizontaal is en naar rechts, wat de bewegingsrichting is.
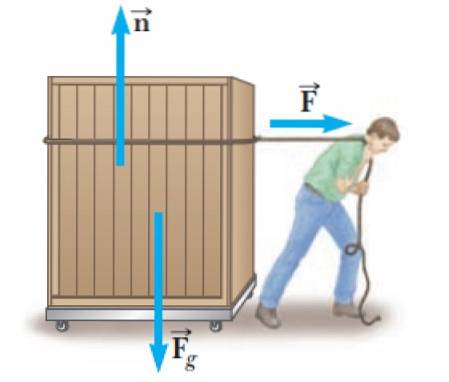
Maar dit is niet de enige kracht die op hem inwerkt, er is ook de normale n, uitgeoefend door het vlakke oppervlak van het verrijdbare platform. En tot slot is er het gewicht ervan: F.g, verticaal naar beneden gericht.
De normaal is een kracht die ontstaat wanneer twee oppervlakken in contact zijn en altijd loodrecht staat op het oppervlak waarop het wordt uitgeoefend. In dit geval oefent het verrijdbare platform een normaal uit op de container.
Een blok dat van een hellend vlak naar beneden glijdt
Bij sommige bureaus is de tafel iets gekanteld om het gemakkelijker te maken om aantekeningen te maken en te lezen. Hij heeft ook een gleuf voor een potloodhouder, maar we hebben het potlood allemaal uit de gleuf op tafel gelegd en we hebben gezien hoe hij over de tafel glijdt.
Welke krachten werken op het potlood?
Dezelfde die werken op het blok dat wordt weergegeven in het volgende free-body-diagram:
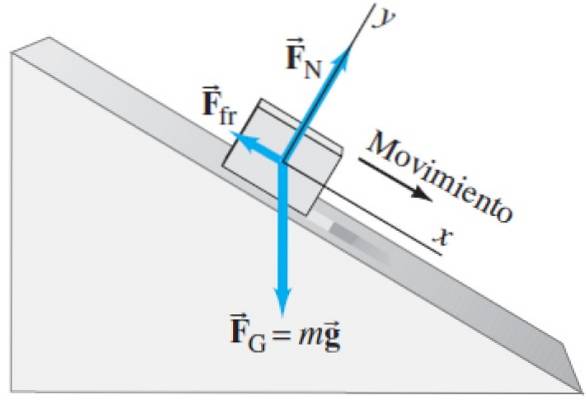
De normale F.N is de kracht die het tafeloppervlak uitoefent op het ondersteunde potlood of blok. In tegenstelling tot het vorige voorbeeld is de normaal niet verticaal, maar schuin. Onthoud dat de normaal de kracht is die de tafel op het blok uitoefent en er loodrecht op staat. Omdat de tafel gekanteld is, ook de normale.
Zoals altijd het gewicht F.g verticaal staat, ongeacht de helling van het systeem.
En tot slot hebben we een nieuwe kracht die werkt, namelijk kinetische wrijving F.vr tussen de tafel en het potlood of blok. Wrijving is ook een contactkracht, maar in tegenstelling tot normaal is het een tangentiële (parallelle) kracht op het oppervlak. Merk ook op dat het altijd in de tegenovergestelde richting van beweging is gericht..
Atwood's machine
De Atwood-machine is een eenvoudige machine die bestaat uit een lichtgewicht, wrijvingsloze katrol op de rail, waar een licht en onrekbaar touw doorheen gaat.
Er worden twee objecten van massa m aan opgehangen1 en Mtwee. Wanneer een van de objecten omhoog gaat, gaat het andere naar beneden, zoals weergegeven in figuur 4a:
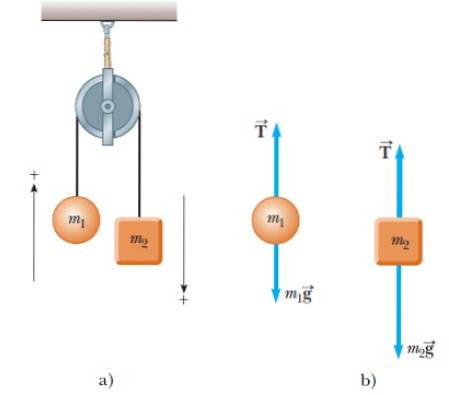
Omdat er twee objecten zijn, wordt voor elk afzonderlijk een vrijlichaamdiagram gemaakt. Voor beide objecten zijn er maar twee krachten: de spanning in de snaar T en de respectievelijke gewichten.
In de figuur wordt elk gewicht rechtstreeks uitgedrukt als het product van massa en versnelling. Van zijn kant wordt de spanning altijd verticaal langs het gespannen touw gericht.
Oefening opgelost
Pas de wetten van Newton toe om de versnelling te bepalen waarmee de massa van de Atwood-machine beweegt die in de vorige sectie wordt getoond.
Oplossing
De tweede wet van Newton stelt dat de som van de krachten gelijk is aan het product van de massa en de versnelling.
De tekenconventie in elke massa kan anders zijn, dus we gaan beweging als een positieve zin nemen, zoals aangegeven in de grafiek, de eerste massa stijgt en de tweede valt.
Bij sommige problemen geeft de verklaring geen informatie, dan moeten de tekens willekeurig worden toegewezen en als het resultaat van de versnelling negatief is, beweegt het massasysteem zich in de tegenovergestelde richting van het aanvankelijk veronderstelde.
-Voor massa 1 (stijgt):
T - m1g = m1naar
-Voor massa 2 (laag):
-T + mtweeg = mtweenaar
Beide vergelijkingen vormen een systeem van lineaire vergelijkingen van twee onbekenden, aangezien de spanning met een ander teken in elke vergelijking verschijnt, voegen we ze eenvoudig term voor term toe en de spanning annuleert:
mtweeg - m1g = m1een + mtweenaar
een = mtweeg - m1g / (m1 + mtwee
Referenties
- Bauer, W. 2011. Physics for Engineering and Sciences. Deel 1. Mc Graw Hill.
- Giancoli, D. 2006. Natuurkunde: principes met toepassingen. 6e. Ed Prentice Hall.
- Serway, R., Vulle, C. 2011. College Physics. 9e Ed. Cengage Learning.
- Tipler, P. (2006) Fysica voor wetenschap en technologie. 5e editie Deel 1. Editorial Reverté.
- Tippens, P. 2011. Fysica: concepten en toepassingen. 7e editie. Mcgraw heuvel



Niemand heeft nog op dit artikel gereageerd.