De verschillen tussen snelheid en snelheid ze bestaan, ook al zijn ze beide verwante fysieke grootheden. In gewone taal wordt de ene term of de andere door elkaar gebruikt alsof het synoniemen zijn, maar in de natuurkunde is het nodig om ze van elkaar te onderscheiden..
Dit artikel definieert beide concepten, wijst op de verschillen en legt aan de hand van voorbeelden uit hoe en wanneer de een of de ander wordt toegepast. Om het te vereenvoudigen beschouwen we een deeltje in beweging en van daaruit zullen we de concepten snelheid en snelheid bespreken.
| Snelheid | Snelheid | |
| Definitie | Het is de afgelegde afstand per tijdseenheid. | Het is de verplaatsing (of verandering van positie) in elke tijdseenheid. |
| Notatie | v | v |
| Wiskundig objecttype | Beklimmen. | Vector. |
| Formule (voor een eindige periode) * | v = Δs / Δt | v = Δr / Δt |
| Formule (voor een bepaald moment) ** | v = ds / dt = s '(t) | v = dr / dt = r '(t) |
| Uitleg van de formule | * Lengte van het afgelegde pad gedeeld door de tijdsperiode die wordt gebruikt om het af te leggen. ** In onmiddellijke snelheid neigt de tijdsperiode naar nul. | * Vectorverplaatsing gedeeld door de tijdspanne waarin de verplaatsing plaatsvond. |
| Kenmerken | Om het uit te drukken, is alleen een positief reëel getal vereist, ongeacht de ruimtelijke dimensies waarin de beweging plaatsvindt.. | Er kan meer dan één reëel getal (positief of negatief) nodig zijn om het uit te drukken, afhankelijk van de ruimtelijke dimensies waarin de beweging plaatsvindt.. |
In bovenstaande tabel zijn verschillende aspecten van snelheid en snelheid samengevat. En dan, om aan te vullen, worden verschillende voorbeelden overwogen die de betrokken concepten en hun relaties illustreren:
Stel dat een rode mier zich langs een rechte lijn beweegt en in de richting zoals aangegeven in de onderstaande afbeelding.
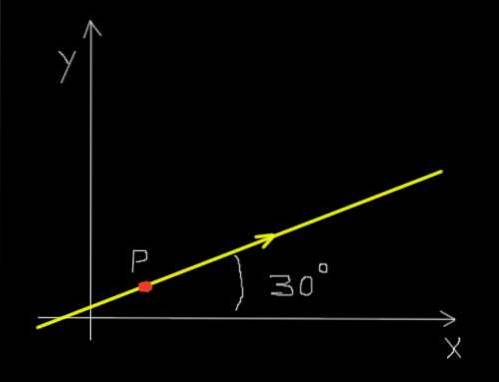
Bovendien beweegt de mier zo gelijkmatig dat hij in een tijdsbestek van 0,25 seconden een afstand van 30 millimeter aflegt..
Bepaal de snelheid en snelheid van de mier.
De snelheid van de mier wordt berekend door de afstand te delen Δs gereisd tussen de time-lapse Δt.
v = Δs / Δt = (30 mm) / (0,25s) = 120 mm / s = 12 cm / s
De snelheid van de mier wordt berekend door de verplaatsing te delen Δr tussen de tijdsperiode waarin de verplaatsing werd gemaakt.
De verplaatsing was 30 mm in de 30 ° -richting ten opzichte van de X-as, of in compacte vorm:
Δr = (30 mm ¦ 30º)
Opgemerkt kan worden dat de verplaatsing bestaat uit een grootte en een richting, aangezien het een vectorgrootheid is. Als alternatief kan de verplaatsing op deze manier worden uitgedrukt volgens de Cartesiaanse componenten X en Y:
Δr = (30 mm * cos (30º); 30 mm * sin (30º)) = (25,98 mm; 15,00 mm)
De snelheid van de mier wordt berekend door de verplaatsing te delen door de tijdsperiode waarin deze is gemaakt:
v Δr/ Δt (25,98 mm / 0,25 sec; 15,00 mm / 0,25 sec) = (103,92; 60,00) mm / sec
Deze snelheid in Cartesische componenten X en Y en in eenheden van cm / s is:
v = (10.392; 6.000) cm / s.
Als alternatief kan de snelheidsvector worden uitgedrukt in zijn polaire vorm (modulus ¦ richting) zoals weergegeven:
v (12 cm / s ¦ 30º).
Opmerking: in dit voorbeeld, aangezien de snelheid constant is, vallen de gemiddelde snelheid en de momentane snelheid samen. De modulus van de momentane snelheid blijkt de momentane snelheid te zijn.
Dezelfde mier in het vorige voorbeeld gaat van A naar B, dan van B naar C en tenslotte van C naar A, volgens het driehoekige pad dat wordt getoond in de volgende afbeelding.
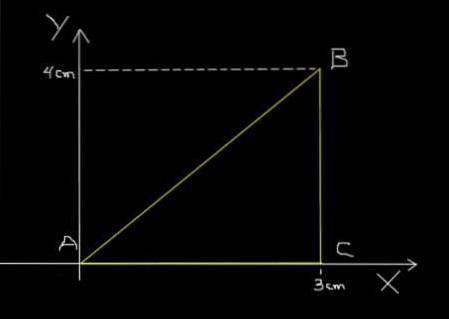
Sectie AB behandelt het in 0.2s; de BC loopt er doorheen in 0.1s en tenslotte CA loopt er doorheen in 0.3s. Bereken de gemiddelde snelheid van de trip ABCA en de gemiddelde snelheid van de trip ABCA.
Om de gemiddelde snelheid van de mier te berekenen, beginnen we met het bepalen van de totale afgelegde afstand:
Δs = 5 cm + 4 cm + 3 cm = 12 cm.
De tijd die voor de hele reis wordt gebruikt, is:
Δt = 0,2 s + 0,1 s + 0,3 s = 0,6 s.
De gemiddelde snelheid van de mier is dus:
v = Δs / Δt = (12 cm) / (0,6s) = 20 cm / s.
Vervolgens wordt de gemiddelde snelheid van de mier in de ABCA-route berekend. In dit geval is de verplaatsing van de mier:
Δr = (0 cm; 0 cm)
Dit komt doordat de offset het verschil is tussen de eindpositie minus de startpositie. Omdat beide posities hetzelfde zijn, is hun verschil nul, wat resulteert in een verplaatsing van nul.
Deze nulverplaatsing werd uitgevoerd in een tijdsperiode van 0,6 s, dus de gemiddelde snelheid van de mier was:
v (0 cm; 0 cm) / 0,6s = (0; 0) cm / s.
Conclusie: gemiddelde snelheid 20 cm / s, maar de gemiddelde snelheid is nul in de ABCA-route.
Een insect beweegt op een cirkel met een straal van 0,2 m met een uniforme snelheid, zodat het, beginnend bij A en aankomend bij B, ¼ van een omtrek aflegt in 0,25 s.
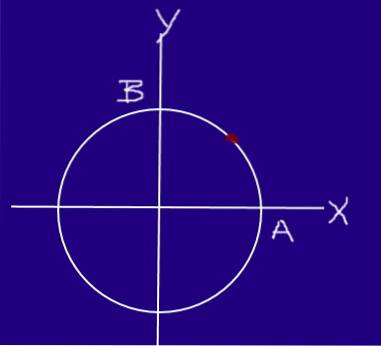
Bepaal de snelheid en snelheid van het insect in sectie AB.
De lengte van de omtrekboog tussen A en B is:
Δs = 2πR / 4 = 2π (0,2 m) / 4 = 0,32 m.
Als we de definitie van gemiddelde snelheid toepassen, hebben we:
v = Δs / Δt = 0,32 m / 0,25 s = 1,28 m / s.
Om de gemiddelde snelheid te berekenen, is het nodig om de verplaatsingsvector tussen de beginpositie A en de eindpositie B te berekenen:
Δr = (0, R) - (R, 0) = (-R, R) = (-0,2, 0,2) m
Door de definitie van gemiddelde snelheid toe te passen, verkrijgen we:
v = Δr/ Δt = (-0,2; 0,2) m / 0,25 s = (-0,8; 0,8) m / s.
De vorige uitdrukking is de gemiddelde snelheid tussen A en B uitgedrukt in Cartesiaanse vorm. Als alternatief kan de gemiddelde snelheid worden uitgedrukt in polaire vorm, dat wil zeggen modulus en richting:
v = ((-0,8) ^ 2 + 0,8 ^ 2) ^ (½) = 1,13 m / s
Richting = arctan (0,8 / (-0,8)) = arctan (-1) = -45º + 180º = 135º ten opzichte van de X-as.
Ten slotte is de gemiddelde snelheidsvector in polaire vorm: v (1,13 m / s ¦ 135º).
Ervan uitgaande dat de starttijd van het insect in het vorige voorbeeld 0 s is vanaf punt A, hebben we dat zijn positievector op elk moment t wordt gegeven door:
r(t) = [R cos ((π / 2) t); R sin ((π / 2) t)].
Bepaal de snelheid en momentane snelheid voor elk moment t.
De momentane snelheid is de afgeleide naar de tijd van de positiefunctie:
v(t) = dr/ dt = [-R (π / 2) sin ((π / 2) t); R (π / 2) cos ((π / 2) t)]
De momentane snelheid is de module van de momentane snelheidsvector:
v (t) = v(t) π R / 2 ^ ½
Niemand heeft nog op dit artikel gereageerd.