
Continu uniforme distributiekarakteristieken, voorbeelden, toepassingen
Een willekeurige variabele heeft een continue uniforme distributie als de kans dat het een waarde aanneemt, binnen een eindig interval [a, b], hetzelfde is voor elk subinterval van gelijke lengte.
Deze verdeling is analoog aan de discrete uniforme verdeling, die aan elk resultaat van het willekeurige experiment dezelfde waarschijnlijkheid toekende, maar in dit geval is de in aanmerking te nemen variabele continu. Het experiment dat bestaat uit het willekeurig kiezen van een reëel getal tussen de waarden a en b, volgt bijvoorbeeld de uniforme verdeling. Hier is de grafiek:
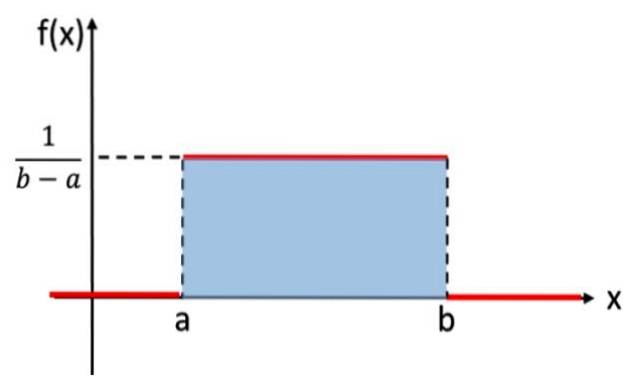
In wiskundige notatie heeft de continue uniforme verdeling een dichtheidsfunctie gedefinieerd als een stuksgewijze of stuksgewijze functie, die kan worden geschreven als:
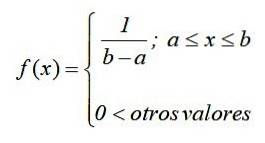
De grafiek van deze functie, bekend als dichtheidscurve of functie, is een rechthoek, daarom wordt de continue gelijkmatige verdeling ook wel rechthoekige indeling y is de eenvoudigste van de continue distributies.
Het gebied onder de grafiek van een kansverdeling is gelijk aan 1 en neemt altijd positieve waarden aan. De uniforme verdeling voldoet aan deze criteria. Het is niet nodig om direct te integreren om te controleren of het gebied 1 is, aangezien het gebied van de gearceerde rechthoek in Figuur 1 kan worden berekend met behulp van de formule:
Oppervlakte = basis x hoogte = (b - a) x [1 / (b - a)] = 1
Het kennen van het gebied onder de dichtheidscurve is erg belangrijk, omdat er een relatie is tussen het gebied en de kans op optreden van een gebeurtenis, die voor deze verdeling wordt bepaald in de volgende paragraaf.
Kenmerken van continue uniforme distributie
De continue gelijkmatige verdeling kenmerkt zich door:
Dichtheidsfunctie
Laat X de continue willekeurige variabele zijn, die behoort tot het interval [a, b], dan:

Distributie functie
De verdelingsfunctie berekent de kans dat de willekeurige variabele X een waarde x krijgt uit de mogelijke waarden van het interval [a, b]. Voor een continue distributie wordt deze over het algemeen als volgt berekend:

In het geval van de continue uniforme verdeling is de kans F (x) gelijk aan het oppervlak van de rechthoek waarvan de basis (x-a) is en de hoogte (b-a):

Wiskundig gezien, als F (x) = Pr (X = x), wordt de volgende functie in delen vastgesteld, volgens het vorige resultaat:

Op deze manier wordt geverifieerd wat eerder werd gezegd: de kans hangt alleen af van de waarde van (x-a) en niet van zijn locatie in het interval [a, b]. De grafiek van de verdelingsfunctie is:
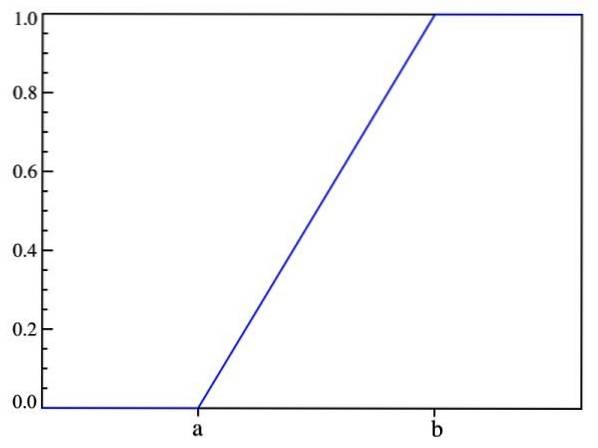
Verwachte waarde, variantie en standaarddeviatie
Na talloze experimenten met de continue willekeurige variabele te hebben gedaan, wordt de gemiddelde waarde ervan opgeroepen verwachte waarde, wordt aangeduid als E (X) en wordt berekend door de volgende integraal:

V (X) = E (Xtwee) - E (X)twee
Daarom:


D (X) = √ V (X)

Mediaan, modus, symmetrie en kurtosis
Het kan gemakkelijk worden geverifieerd dat de mediaan, de centrale waarde van de uniforme verdeling, gelijk is aan het gemiddelde, en aangezien er geen waarde is die zich meer herhaalt dan andere, omdat ze allemaal even waarschijnlijk zijn in het interval [a, b] , mode bestaat niet.
Wat betreft symmetrie: de uniforme verdeling is symmetrisch en de kurtosis, de mate waarin de waarden geconcentreerd zijn rond het midden, is -6/5.
Voorbeelden
Door continue distributie kunnen verschillende situaties worden gemodelleerd, waardoor hun gedrag kan worden voorspeld. Hier zijn enkele voorbeelden:
voorbeeld 1
Een bedrijf dat elektriciteit levert, levert spanningsniveaus die gelijkmatig verdeeld zijn, tussen 123,0 V en 125,0 V. Dit betekent dat het in het stopcontact voor huishoudelijk gebruik mogelijk is om elke spanningswaarde te verkrijgen die tot dat bereik behoort..
Dus, zoals hierboven te zien is, is de grafiek van de dichtheidsfunctie de rechthoek in rood:

Het berekenen van de kans op een spanning binnen het gegeven interval is heel eenvoudig, wat is bijvoorbeeld de kans dat het bedrijf een spanning zendt die lager is dan 123,5 V?
Deze kans is gelijk aan de oppervlakte van de rechthoek in blauw gearceerd:
P (X<123.5) = (123.5 −123.0)x 0.5 = 0.25
En wat is de kans dat de geleverde spanning groter is dan 124,0 V?
Aangezien de totale oppervlakte gelijk is aan 1, is de gezochte kans:
P (X> 124,0 V) = 1 - (1 × 0,5) = 0,5
Logisch, aangezien 124,0 precies de waarde in het midden van het interval is.
Voorbeeld 2
Een bepaalde willekeurige variabele X heeft een uniforme verdeling in het interval [0,100]. Besluiten:
a) De kans dat de waarde van X kleiner is dan 22.
b) De kans dat X waarden tussen 20 en 35 aanneemt.
c) De verwachte waarde, variantie en standaarddeviatie van deze verdeling.
Antwoord op
Het wordt op dezelfde manier bepaald als in het vorige voorbeeld, maar eerst moeten we de hoogte van de rechthoek bepalen, waarbij we bedenken dat de totale oppervlakte gelijk moet zijn aan 1:
Oppervlakte = 100 × hoogte = 1
Daarom heeft de rechthoek een hoogte gelijk aan 1/100 = 0,01
P (X<22) = 22×0.01 = 0.22
Antwoord b
De gevraagde kans is gelijk aan de oppervlakte van de rechthoek waarvan de breedte (35 - 20) is en waarvan de hoogte 0,01 is:
P (22 Als u liever rechtstreeks naar de bovenstaande verdelingsfunctie gaat, hoeft u alleen de waarden in te vervangen: P (20≤X≤35) = F (35) -F (20) Met F (x) gegeven door: F (x) = (x-a) / (b-a) De in te voeren waarden zijn: a = 0 b = 100 F (35) = (35-0) / (100-0) = 0,35 F (20) = (20-0) / (100-0) = 0,20 P (20≤X≤35) = 0,35-0,20 = 0,15 De verwachte waarde is: E (X) = (a + b) / 2 = (100 + 0) / 2 = 50 De variantie is: V (X) = (b-a)twee/ 12 = (100-0)twee/ 12 = 833,33 En de standaarddeviatie is: D (X) = √833,33 = 28,87 Deze verdeling is handig bij het uitvoeren van statistische simulatieprocessen of bij het werken aan gebeurtenissen waarvan de frequentie regelmatig is.. Sommige programmeertalen genereren willekeurige getallen tussen 0 en 1, en zoals blijkt uit de voorgaande voorbeelden, is de gevolgde kansverdeling uniform. In dit geval is het te overwegen interval [0,1]. Als je een experiment hebt waarin de gebeurtenissen regelmaat hebben, zoals eerder uitgelegd, kun je in principe aan elke gebeurtenis dezelfde kans op voorkomen toekennen. In dit geval biedt het probabilistische model van uniforme distributie informatie voor de analyse.. De uniforme verdeling wordt ook gebruikt voor het afronden van de verschillen tussen de waargenomen waarden en de reële waarden van een variabele, uitgaande van een uniforme verdeling van de fout in een bepaald interval, volgens afronding, meestal van -0,5 tot +0,5..Antwoord c
Toepassingen
Genereren van willekeurige getallen
Bemonstering van willekeurige distributies
Fouten afronden
Referenties



Niemand heeft nog op dit artikel gereageerd.