
Thermische evenwichtsvergelijkingen, toepassingen, oefeningen
Het thermisch evenwicht van twee lichamen die in thermisch contact zijn, is de toestand die wordt bereikt na een tijd die lang genoeg is om de temperatuur van beide lichamen gelijk te maken.
In de thermodynamica wordt thermisch contact van twee lichamen (of twee thermodynamische systemen) opgevat als een situatie waarin de lichamen mechanisch contact hebben of gescheiden zijn maar in contact staan met een oppervlak dat alleen de doorgang van warmte van het ene lichaam naar het andere toelaat (diathermische oppervlakte).
-

Figuur 1. Na een tijdje zullen het ijs en de drank hun thermisch evenwicht bereiken. Bron: pixabay
Bij thermisch contact mag er geen chemische reactie optreden tussen de systemen die in contact staan. Er mag alleen warmte-uitwisseling zijn.
Alledaagse situaties waarin er warmte-uitwisseling is, doen zich voor bij systemen zoals de koude drank en het glas, de hete koffie en de theelepel, of het lichaam en de thermometer, naast vele andere voorbeelden..
Artikel index
- 1 Wanneer zijn twee of meer systemen in thermisch evenwicht??
- 2 Vergelijkingen van thermisch evenwicht
- 2.1 Evenwichtstemperatuur
- 2.2 Thermisch contact met faseverandering
- 3 Toepassingen
- 3.1 -Oefening 1
- 4 Opgeloste oefeningen
- 4.1 -Oefening 2
- 4.2 Oefening 3
- 4.3 -Oefening 4
- 5 referenties
Wanneer twee of meer systemen in thermisch evenwicht zijn?
De tweede wet van de thermodynamica stelt dat warmte altijd van het lichaam met de hoogste temperatuur naar het lichaam met de laagste temperatuur gaat. De warmteoverdracht stopt zodra de temperaturen gelijk worden en de toestand van thermisch evenwicht is bereikt..
De praktische toepassing van thermisch evenwicht is de thermometer. Een thermometer is een apparaat dat zijn eigen temperatuur meet, maar dankzij thermisch evenwicht kunnen we de temperatuur van andere lichamen kennen, zoals die van een persoon of dier..
De kwikkolomthermometer wordt in thermisch contact met het lichaam geplaatst, bijvoorbeeld onder de tong, en er wordt voldoende tijd gewacht totdat het thermisch evenwicht tussen het lichaam en de thermometer is bereikt en dat de aflezing niet verder varieert..
Wanneer dit punt is bereikt, is de temperatuur van de thermometer dezelfde als die van het lichaam.
De nulwet van de thermodynamica stelt dat als een lichaam A in thermisch evenwicht is met een lichaam C en datzelfde lichaam C in thermisch evenwicht is met B, dan zijn A en B in thermisch evenwicht, zelfs als er geen thermisch contact is tussen A en B..
Daarom concluderen we dat twee of meer systemen in thermisch evenwicht zijn wanneer ze dezelfde temperatuur hebben.
Thermische evenwichtsvergelijkingen
We gaan uit van een lichaam A met begintemperatuur Ta in thermisch contact met een ander lichaam B met begintemperatuur Tb. We nemen ook aan dat Ta> Tb, dan wordt volgens de tweede wet de warmte overgedragen van A naar B.
Na enige tijd zal een thermisch evenwicht worden bereikt en zullen beide lichamen dezelfde eindtemperatuur Tf hebben. Dit heeft een tussenwaarde bij Ta en Tb, dat wil zeggen Ta> Tf> Tb.
De hoeveelheid warmte Qa die van A naar B wordt overgedragen, is Qa = Ma Ca (Tf - Ta), waarbij Ma de massa van lichaam A is, Ca de warmtecapaciteit per massa-eenheid van A en (Tf - Ta) het temperatuurverschil. Als Tf kleiner is dan Ta, dan is Qa negatief, wat aangeeft dat het lichaam A warmte afgeeft.
Evenzo hebben we voor het lichaam B dat Qb = Mb Cb (Tf - Tb); en als Tf groter is dan Tb, dan is Qb positief, wat aangeeft dat lichaam B warmte ontvangt. Omdat lichaam A en lichaam B in thermisch contact met elkaar staan, maar geïsoleerd zijn van de omgeving, moet de totale hoeveelheid uitgewisselde warmte nul zijn: Qa + Qb = 0
Dan is Ma Ca (Tf - Ta) + Mb Cb (Tf - Tb) = 0
Evenwichtstemperatuur
Door deze uitdrukking te ontwikkelen en op te lossen voor de temperatuur Tf wordt de eindtemperatuur van thermisch evenwicht verkregen.
-

Figuur 2. Uiteindelijke evenwichtstemperatuur. Bron: zelf gemaakt
Tf = (Ma Ca Ta + Mb Cb Tb) / (Ma Ca + Mb Cb).
Beschouw als een specifiek geval het geval dat de lichamen A en B identiek zijn in massa en warmtecapaciteit, in dit geval zal de evenwichtstemperatuur zijn:
Tf = (Ta + Tb) / 2 ↔ als Ma = Mb en Ca = Cb.
Thermisch contact met faseverandering
In sommige situaties komt het voor dat wanneer twee lichamen in thermisch contact worden geplaatst, de warmte-uitwisseling de toestand of fase in een van hen verandert. Als dit gebeurt, moet er rekening mee worden gehouden dat er tijdens de faseverandering geen temperatuurverandering is in het lichaam dat zijn toestand wijzigt.
Als de faseverandering van een van de lichamen in thermisch contact optreedt, wordt het concept van latente warmte L toegepast, wat de energie per massa-eenheid is die nodig is voor de toestandsverandering:
Q = L ∙ M
Om bijvoorbeeld 1 kg ijs te smelten bij 0 ° C is 333,5 kJ / kg vereist en deze waarde is de latente warmte L van het smelten van ijs.
Tijdens het smelten verandert het van vast water in vloeibaar water, maar dat water behoudt tijdens het smeltproces dezelfde temperatuur als ijs..
Toepassingen
Thermische balans maakt deel uit van het dagelijks leven. Laten we deze situatie bijvoorbeeld in detail bekijken:
-Oefening 1
Een persoon wil baden in warm water van 25 ° C. Doe in een emmer 3 liter koud water van 15 ° C en verwarm in de keuken water tot 95 ° C.
Hoeveel liter heet water moet je toevoegen aan de emmer koud water om de gewenste eindtemperatuur te krijgen?
Oplossing
Stel dat A koud water is en B heet water:
-
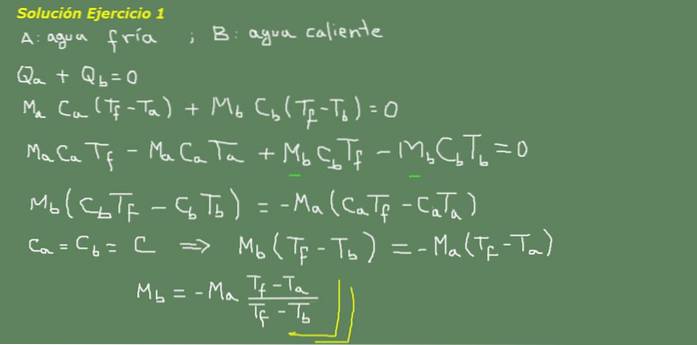
Figuur 3. Oplossing voor oefening 3. Bron: eigen uitwerking.
We stellen de vergelijking van het thermisch evenwicht voor, zoals aangegeven op het bord in figuur 3 en van daaruit lossen we de massa van water Mb op.
De aanvankelijke massa koud water kan worden verkregen doordat de dichtheid van het water bekend is, namelijk 1 kg per liter. Dat wil zeggen, we hebben 3 kg koud water.
Ma = 3 kg
Dan
Mb = - 3 kg * (25 ° C - 15 ° C) / (25 ° C - 95 ° C) = 0,43 kg
Dan is 0,43 liter heet water voldoende om uiteindelijk 3,43 liter warm water van 25 ° C te krijgen.
Opgeloste oefeningen
-Oefening 2
Een stuk metaal met een massa van 150 g en een temperatuur van 95 ° C wordt in een bak met een halve liter water van 18 ° C gebracht. Na een tijdje is het thermisch evenwicht bereikt en is de temperatuur van het water en het metaal 25 ° C.
Stel dat de bak met het water en het stuk metaal een gesloten thermoskan is die geen warmte-uitwisseling met de omgeving toelaat.
Verkrijg de soortelijke warmte van het metaal.
Oplossing
Eerst berekenen we de warmte die door het water wordt opgenomen:
Qa = Ma Ca (Tf - Ta)
Qa = 500 g 1cal / (g ° C) (25 ° C - 18 ° C) = 3500 calorieën.
Dat is dezelfde warmte die door het metaal wordt gegeven:
Qm = 150 g Cm (25 ° C - 95 ° C) = -3500 calorieën.
Zodat we de warmtecapaciteit van het metaal kunnen krijgen:
Cm = 3500 cal / (150 g 70 ° C) = ⅓ cal / (g ° C).
Oefening 3
Je hebt 250 c.c. van water bij 30 ° C. Aan dat water dat in een isolerende thermoskan zit, wordt 25 g ijsblokjes van 0 ° C toegevoegd om het te koelen.
Bepaal de evenwichtstemperatuur; dat wil zeggen, de temperatuur die zal blijven als al het ijs is gesmolten en het ijswater is opgewarmd om in eerste instantie overeen te komen met die van het water in het glas.
Oplossing 3
Deze oefening kan in drie fasen worden opgelost:
- De eerste is het smelten van ijs dat warmte absorbeert van het oorspronkelijke water om te smelten en water te worden..
- Vervolgens wordt de temperatuurdaling in het aanvankelijke water berekend, omdat het warmte heeft opgegeven (Qced<0) para fundir el hielo.
- Ten slotte moet het gesmolten water (afkomstig van het ijs) thermisch in evenwicht worden gebracht met het water dat aanvankelijk bestond..
-

Figuur 4. Oplossing voor oefening 3. Bron: eigen uitwerking.
Laten we de warmte berekenen die nodig is voor het smelten van ijs:
Qf = L * Mh = 333,5 kJ / kg * 0,025 kg = 8,338 kJ
Vervolgens is de warmte die het water geeft om het ijs te smelten Qced = -Qf
Deze warmte die door het water wordt afgegeven, verlaagt de temperatuur tot een waarde T 'die we als volgt kunnen berekenen:
T '= T0 - Qf / (Ma * Ca) = 22,02 ° C
Waar Ca de warmtecapaciteit van water is: 4,18 kJ / (kg ° C).
Ten slotte zal de oorspronkelijke watermassa die nu 22,02 ° C is, warmte afgeven aan de massa gesmolten water van het ijs dat op 0 ° C staat..
Uiteindelijk wordt de evenwichtstemperatuur Te na voldoende tijd bereikt:
Te = (Ma * T '+ Mh * 0 ° C) / (Ma + Mh) = (0,25 kg * 22,02 ° C + 0,025 kg * 0 ° C) / (0,25 kg + 0,025 kg).
Eindelijk het verkrijgen van de evenwichtstemperatuur:
Te = 20,02 ° C.
-Oefening 4
Een stuk lood van 0,5 kg komt uit de oven bij een temperatuur van 150 ° C, wat ruim onder het smeltpunt ligt. Dit stuk wordt in een bak met 3 liter water bij kamertemperatuur van 20 ° C geplaatst. Bepaal de uiteindelijke evenwichtstemperatuur.
Bereken ook:
- Hoeveelheid warmte geleverd door lood aan water.
- Hoeveelheid warmte opgenomen door water.
Gegevens:
Soortelijke warmte van lood: Cp = 0,03 cal / (g ° C); soortelijke warmte van water: Ca = 1 cal / (g ° C).
Oplossing
Eerst bepalen we de uiteindelijke evenwichtstemperatuur Te:
Te = (Ma Ca Ta + Mp Cp Tp) / (Ma Ca + Mp Cp)
Te = 20,65 ° C
Dan is de hoeveelheid warmte die door lood vrijkomt:
Qp = Mp Cp (Te - Tp) = -1,94 x 10³ cal.
De hoeveelheid warmte die door het water wordt opgenomen, is:
Qa = Ma Ca (Te - Ta) = + 1,94x 10³ cal.
Referenties
- Atkins, P. 1999. Physical Chemistry. Omega-edities.
- Bauer, W. 2011. Physics for Engineering and Sciences. Deel 1. Mc Graw Hill.
- Giancoli, D. 2006. Natuurkunde: principes met toepassingen. 6e… Ed Prentice Hall.
- Hewitt, Paul. 2012. Conceptuele fysische wetenschappen. 5e. Ed Pearson.
- Resnick, R. (1999). Fysiek. Vol. 1. 3e uitgave in het Spaans. Compañía Redactioneel Continental S.A. door C.V.
- Rex, A. 2011. Fundamentals of Physics. Pearson.
- Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. Ed. Deel 1.
- Serway, R., Jewett, J. (2008). Physics for Science and Engineering. Deel 1. 7e. Ed. Cengage Learning.



Niemand heeft nog op dit artikel gereageerd.