De cumulatieve frequentie is de som van de absolute frequenties f, van de laagste tot degene die overeenkomt met een bepaalde waarde van de variabele. De absolute frequentie is op zijn beurt het aantal keren dat een waarneming in de dataset voorkomt.
Het is duidelijk dat de studievariabele sorteerbaar moet zijn. En aangezien de geaccumuleerde frequentie wordt verkregen door de absolute frequenties op te tellen, blijkt dat de geaccumuleerde frequentie tot de laatste gegevens moet samenvallen met het totaal ervan. Anders zit er een fout in de berekeningen.
Gewoonlijk wordt de cumulatieve frequentie aangeduid als Fik (of soms nik), om het te onderscheiden van de absolute frequentie fik en het is belangrijk om er een kolom voor toe te voegen in de tabel waarmee de gegevens zijn georganiseerd, bekend als frequentietabel.
Dit maakt het onder andere gemakkelijker om bij te houden hoeveel data tot een bepaalde waarneming is geteld..
A Fik het is ook bekend als absolute cumulatieve frequentie. Indien gedeeld door de totale gegevens, hebben we de relatieve cumulatieve frequentie, waarvan het uiteindelijke bedrag gelijk moet zijn aan 1.
Artikel index
De cumulatieve frequentie van een bepaalde waarde van variabele Xik is de som van de absolute frequenties f van alle waarden kleiner dan of gelijk aan:
F.ik = f1 + F.twee + F.3 +... fik
Door alle absolute frequenties op te tellen, wordt het totale aantal gegevens N verkregen, dat wil zeggen:
F.1 + F.twee + F.3 ++ F.n = N
De vorige bewerking is samengevat geschreven door middel van het sommatiesymbool:
∑ F.ik = N
De volgende frequenties kunnen ook worden verzameld:
-Relatieve frequentie: wordt verkregen door de absolute frequentie f te delenik tussen de totale gegevens N:
F.r = fik / N
Als de relatieve frequenties van de laagste tot de frequentie die overeenkomt met een bepaalde waarneming worden opgeteld, hebben we de cumulatieve relatieve frequentie. De laatste waarde moet gelijk zijn aan 1.
-Percentage cumulatieve relatieve frequentie: de geaccumuleerde relatieve frequentie wordt vermenigvuldigd met 100%.
F. = (fik / N) x 100%
Deze frequenties zijn nuttig om het gedrag van de gegevens te beschrijven, bijvoorbeeld bij het vinden van de maten van centrale tendens.
Om de geaccumuleerde frequentie te verkrijgen, is het noodzakelijk om de gegevens te ordenen en ze in een frequentietabel te ordenen. De procedure wordt geïllustreerd in de volgende praktijksituatie:
-In een online winkel die mobiele telefoons verkoopt, vertoonde het verkooprecord van een bepaald merk voor de maand maart de volgende waarden per dag:
1; twee; 1; 3; 0; 1; 0; twee; 4; twee; 1; 0; 3; 3; 0; 1; twee; 4; 1; twee; 3; twee; 3; 1; twee; 4; twee; 1; 5; 5; 3
De variabele is de aantal verkochte telefoons per dag en het is kwantitatief. De gegevens die op deze manier worden gepresenteerd, zijn niet zo gemakkelijk te interpreteren, de eigenaren van de winkel zijn bijvoorbeeld misschien geïnteresseerd in het weten of er een trend is, zoals dagen van de week waarop de verkoop van dat merk hoger is..
Informatie zoals deze en meer kan worden verkregen door de gegevens op een geordende manier weer te geven en de frequenties te specificeren..
Om de cumulatieve frequentie te berekenen, worden de gegevens eerst geordend:
0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; twee; twee; twee; twee; twee; twee; twee; twee; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5
Vervolgens wordt een tafel gebouwd met de volgende informatie:
-De eerste kolom aan de linkerkant met het aantal verkochte telefoons, tussen 0 en 5 en in oplopende volgorde.
-Tweede kolom: absolute frequentie, het aantal dagen dat 0 telefoons, 1 telefoon, 2 telefoons enzovoort zijn verkocht.
-Derde kolom: de geaccumuleerde frequentie, bestaande uit de som van de vorige frequentie plus de frequentie van de gegevens waarmee rekening moet worden gehouden.
Deze kolom begint met de eerste gegevens in de absolute frequentiekolom, in dit geval is het 0. Voor de volgende waarde, tel deze op bij de vorige. Het gaat zo door totdat de laatste gegevens van de verzamelde frequentie zijn bereikt, die moeten samenvallen met de totale gegevens.
De volgende tabel toont de variabele "aantal verkochte telefoons per dag", de absolute frequentie en de gedetailleerde berekening van de geaccumuleerde frequentie.
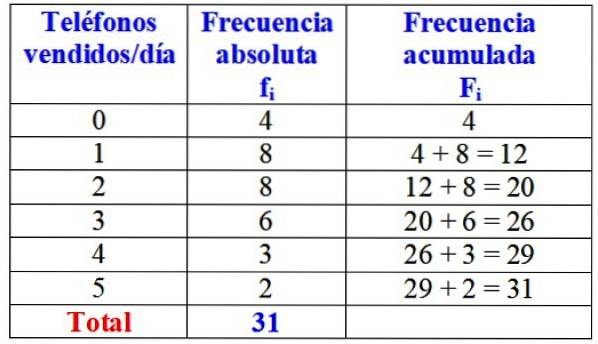
Op het eerste gezicht zou kunnen worden gesteld dat van het merk in kwestie bijna altijd een of twee telefoons per dag worden verkocht, aangezien de hoogste absolute frequentie 8 dagen is, wat overeenkomt met deze waarden van de variabele. Slechts gedurende 4 dagen van de maand verkochten ze geen enkele telefoon.
Zoals opgemerkt, is de tabel gemakkelijker te onderzoeken dan de individuele gegevens die oorspronkelijk zijn verzameld.
Een cumulatieve frequentieverdeling is een tabel met de absolute frequenties, de cumulatieve frequenties, de cumulatieve relatieve frequenties en het cumulatieve percentage frequenties..
Hoewel het voordeel is om de gegevens in een tabel zoals de vorige te ordenen, is het mogelijk dat als het aantal gegevens erg groot is, het niet voldoende is om ze te ordenen zoals hierboven weergegeven, want als er veel frequenties zijn, wordt het nog steeds moeilijk om interpreteren.
Het probleem kan worden verholpen door een frequentieverdeling met intervallen, een handige procedure wanneer de variabele een groot aantal waarden aanneemt of als het een continue variabele is.
Hier zijn de waarden gegroepeerd in intervallen van gelijke amplitude, genaamd klasse. De lessen kenmerken zich door:
-Klasse limiet: zijn de uiterste waarden van elk interval, er zijn er twee, de bovengrens en de ondergrens. Over het algemeen hoort de bovengrens niet bij het interval maar bij de volgende, terwijl de ondergrens wel hoort.
-Klasse cijfer: is het middelpunt van elk interval, en wordt genomen als de representatieve waarde ervan.
-Klasse breedte: Het wordt berekend door de waarde van de grootste en kleinste gegevens (bereik) af te trekken en te delen door het aantal klassen:
Klasse breedte = bereik / aantal klassen
De uitwerking van de frequentieverdeling wordt hieronder toegelicht..
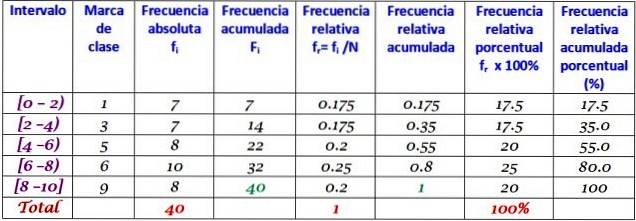
Deze dataset komt overeen met 40 punten van een wiskundetoets, op een schaal van 0 tot 10:
0; 0; 0; 1; 1; 1; 1; twee; twee; twee; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 9; 9; 10; 10.
Een frequentieverdeling kan gemaakt worden met een bepaald aantal klassen, bijvoorbeeld 5 klassen. Houd er rekening mee dat bij het gebruik van veel klassen de gegevens niet gemakkelijk te interpreteren zijn en het gevoel van het uitvoeren van de groepering verloren gaat.
En als ze daarentegen in zeer weinige groepen worden gegroepeerd, wordt de informatie verwaterd en gaat een deel ervan verloren. Het hangt allemaal af van de hoeveelheid gegevens die u heeft.
In dit voorbeeld is het een goed idee om twee scores in elk interval te hebben, aangezien er 10 scores zijn en er zullen 5 klassen worden gemaakt. Het bereik is de aftrekking tussen het hoogste en laagste cijfer, waarbij de klassebreedte is:
Klasse breedte = (10-0) / 5 = 2
De intervallen zijn links gesloten en rechts open (behalve de laatste), die wordt gesymboliseerd door respectievelijk vierkante haken en haakjes. Ze hebben allemaal dezelfde breedte, maar het is niet verplicht, hoewel dit meestal het geval is.
Elk interval bevat een bepaald aantal elementen of absolute frequentie, en in de volgende kolom staat de geaccumuleerde frequentie waarin de som wordt gedragen. De tabel toont ook de relatieve frequentie fr (absolute frequentie tussen het totale aantal gegevens) en het percentage relatieve frequentie fr × 100%.
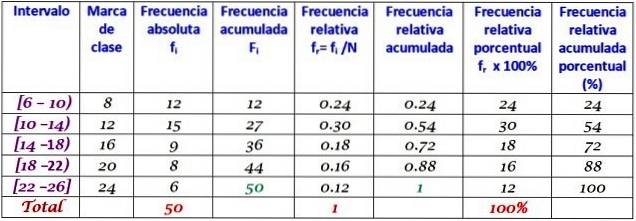
Een bedrijf belde dagelijks zijn klanten tijdens de eerste twee maanden van het jaar. De gegevens zijn als volgt:
6, 12, 7, 15, 13, 18, 20, 25, 12, 10, 8, 13, 15, 6, 9, 18, 20, 24, 12, 7, 10, 11, 13, 9, 12, 15, 18, 20, 13, 17, 23, 25, 14, 18, 6, 14, 16, 9, 6, 10, 12, 20, 13, 17, 14, 26, 7, 12, 24, 7
Groepeer in 5 klassen en bouw de tafel met de frequentieverdeling.
De klassebreedte is:
(26-6) / 5 = 4
Probeer erachter te komen voordat u het antwoord ziet.
Niemand heeft nog op dit artikel gereageerd.