De homoscedasticiteit in een voorspellend statistisch model komt het voor als in alle gegevensgroepen van een of meer waarnemingen de variantie van het model ten opzichte van de verklarende (of onafhankelijke) variabelen constant blijft.
Een regressiemodel kan homoscedastisch zijn of niet, in dat geval spreken we van heteroscedasticiteit.
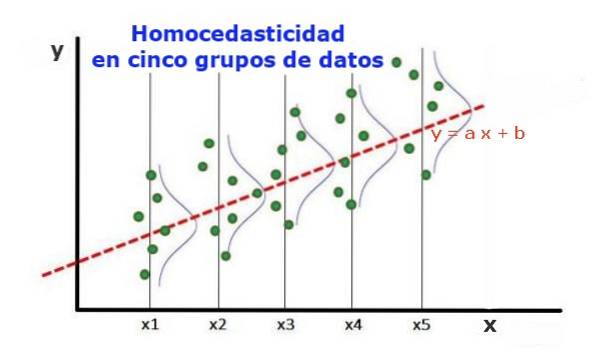
Een statistisch regressiemodel van verschillende onafhankelijke variabelen wordt homoscedastisch genoemd, alleen als de variantie van de fout van de voorspelde variabele (of de standaarddeviatie van de afhankelijke variabele) uniform blijft voor verschillende groepen waarden van de verklarende of onafhankelijke variabelen.
In de vijf datagroepen in figuur 1 is de variantie in elke groep berekend ten opzichte van de waarde geschat door de regressie, waardoor deze in elke groep hetzelfde is. Verder wordt aangenomen dat de gegevens de normale verdeling volgen.
Op grafisch niveau betekent dit dat de punten gelijkelijk verspreid of verspreid zijn over de waarde die wordt voorspeld door de regressie-aanpassing, en dat het regressiemodel dezelfde fout en geldigheid heeft voor het bereik van de verklarende variabele..
Artikel index
Om het belang van homoscedasticiteit in voorspellende statistieken te illustreren, is het nodig om te contrasteren met het tegenovergestelde fenomeen, heteroscedasticiteit..
In het geval van figuur 1, waarin sprake is van homoscedasticiteit, geldt dat:
Var ((y1-Y1); X1) ≈ Var ((y2-Y2); X2) ≈… Var ((y4-Y4); X4)
Waar Var ((yi-Yi); Xi) de variantie vertegenwoordigt, vertegenwoordigt het paar (xi, yi) gegevens uit groep i, terwijl Yi de waarde is die wordt voorspeld door de regressie voor de gemiddelde waarde Xi van de groep. De variantie van de n gegevens uit groep i wordt als volgt berekend:
Var ((yi-Yi); Xi) = ∑j (yij - Yi) ^ 2 / n
Integendeel, wanneer heteroscedasticiteit optreedt, is het regressiemodel mogelijk niet geldig voor de hele regio waarin het werd berekend. Figuur 2 toont een voorbeeld van deze situatie.
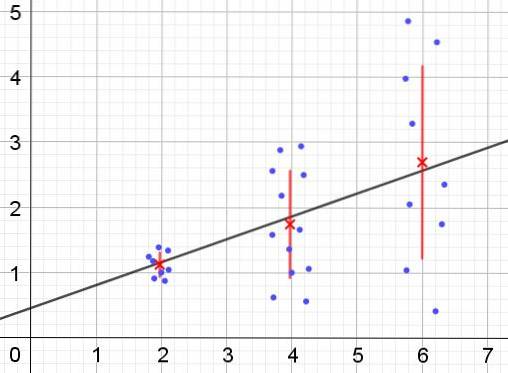
Figuur 2 geeft drie groepen gegevens weer en de pasvorm van de set met behulp van een lineaire regressie. Opgemerkt moet worden dat de gegevens in de tweede en derde groep meer verspreid zijn dan in de eerste groep. De grafiek in figuur 2 toont ook de gemiddelde waarde van elke groep en zijn foutbalk ± σ, met de σ standaarddeviatie van elke groep gegevens. Houd er rekening mee dat de standaarddeviatie σ de vierkantswortel is van de variantie.
Het is duidelijk dat in het geval van heteroscedasticiteit de regressieschattingsfout verandert in het waardenbereik van de verklarende of onafhankelijke variabele, en in de intervallen waarin deze fout erg groot is, de regressievoorspelling onbetrouwbaar of niet toepasbaar is..
In een regressiemodel moeten de fouten of residuen (en -Y) met gelijke variantie (σ ^ 2) worden verdeeld over het interval van waarden van de onafhankelijke variabele. Om deze reden moet een goed regressiemodel (lineair of niet-lineair) de homoscedasticiteitstest doorstaan..
De punten weergegeven in figuur 3 komen overeen met de gegevens van een studie die een relatie zoekt tussen de prijzen (in dollars) van de huizen als functie van de grootte of oppervlakte in vierkante meters.
Het eerste te testen model is dat van een lineaire regressie. In de eerste plaats wordt opgemerkt dat de determinatiecoëfficiënt R ^ 2 van de pasvorm vrij hoog is (91%), dus kan worden aangenomen dat de pasvorm bevredigend is..
Twee regio's kunnen echter duidelijk worden onderscheiden van de aanpassingsgrafiek. Een van hen, die rechts ingesloten in een ovaal, vervult homoscedasticiteit, terwijl de regio aan de linkerkant geen homoscedasticiteit heeft.
Dit betekent dat de voorspelling van het regressiemodel adequaat en betrouwbaar is in het bereik tussen 1800 m ^ 2 tot 4800 m ^ 2, maar buiten dit gebied zeer ontoereikend. In de heteroscedastische zone is niet alleen de fout erg groot, maar ook lijken de gegevens een andere trend te volgen dan voorgesteld door het lineaire regressiemodel..
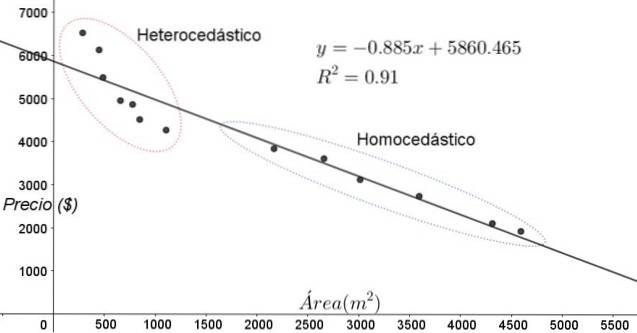
Het spreidingsdiagram van de gegevens is de eenvoudigste en meest visuele test van hun homoscedasticiteit, maar in gevallen waarin het niet zo duidelijk is als in het voorbeeld in figuur 3, is het nodig om gebruik te maken van grafieken met hulpvariabelen..
Om de gebieden te scheiden waar aan homoscedasticiteit wordt voldaan en waar niet, worden de gestandaardiseerde variabelen ZRes en ZPred geïntroduceerd:
ZRes = Abs (y - Y) / σ
ZPred = Y / σ
Opgemerkt moet worden dat deze variabelen afhankelijk zijn van het toegepaste regressiemodel, aangezien Y de waarde is van de regressievoorspelling. Hieronder ziet u de spreidingsplot ZRes versus ZPred voor hetzelfde voorbeeld:
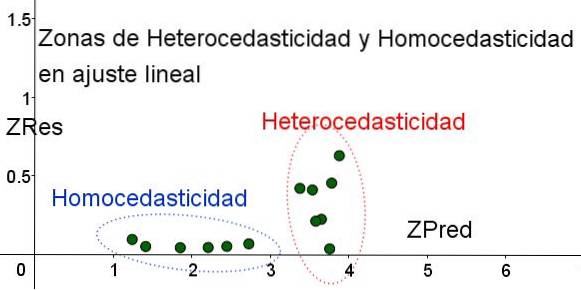
In de grafiek in Figuur 4 met de gestandaardiseerde variabelen is het gebied waar de restfout klein en uniform is duidelijk gescheiden van het gebied waar dat niet het geval is. In de eerste zone wordt aan homoscedasticiteit voldaan, terwijl in het gebied waar de restfout zeer variabel en groot is, aan heteroscedasticiteit wordt voldaan..
Regressie-aanpassing wordt toegepast op dezelfde groep gegevens in figuur 3, in dit geval is de aanpassing niet-lineair, aangezien het gebruikte model een potentiële functie bevat. Het resultaat wordt weergegeven in de volgende afbeelding:
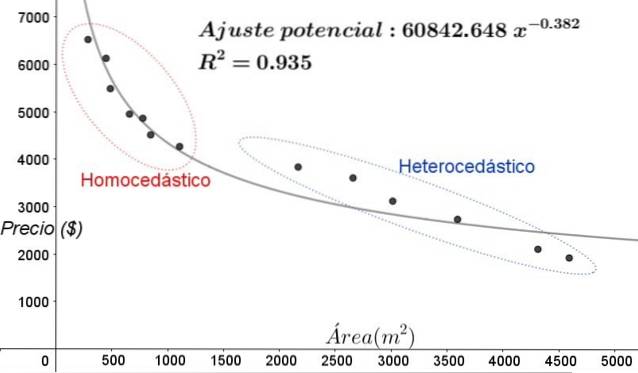
In de grafiek in figuur 5 moeten de homoscedastische en heteroscedastische zones duidelijk worden aangegeven. Er moet ook worden opgemerkt dat deze zones werden verwisseld met betrekking tot de zones die werden gevormd in het lineaire fit-model.
In de grafiek van figuur 5 is het duidelijk dat zelfs als er een vrij hoge coëfficiënt van bepaling van de fit is (93,5%), het model niet toereikend is voor het hele interval van de verklarende variabele, aangezien de gegevens voor waarden groter dan 2000 m ^ 2 aanwezige heteroscedasticiteit.
Een van de niet-grafische tests die het meest wordt gebruikt om te verifiëren of aan homoscedasticiteit is voldaan of niet, is de Breusch-Pagan-test.
Niet alle details van deze test zullen in dit artikel worden gegeven, maar de fundamentele kenmerken en de stappen ervan worden in grote lijnen uiteengezet:
De meeste statistische softwarepakketten zoals: SPSS, MiniTab, R, Python Pandas, SAS, StatGraphic en verschillende andere bevatten de homoscedasticiteitstest van Breusch-Pagan. Een andere test om de uniformiteit van variantie te verifiëren is de Levene-test.
Niemand heeft nog op dit artikel gereageerd.