
Formule en vergelijkingen van de wet van Ampère, bewijs, oefeningen
De De wet van Ampère stelt dat de circulatie van de magnetische inductievector B. is evenredig met de intensiteit I van de stroom die er doorheen vloeit.
Op zijn beurt de circulatie van B. is de som van alle producten tussen de tangentiële component B en de lengte van een klein segment Δℓ van een gesloten curve C, rond een circuit. In wiskundige termen is het als volgt geschreven:
∑ B .Δℓ ik
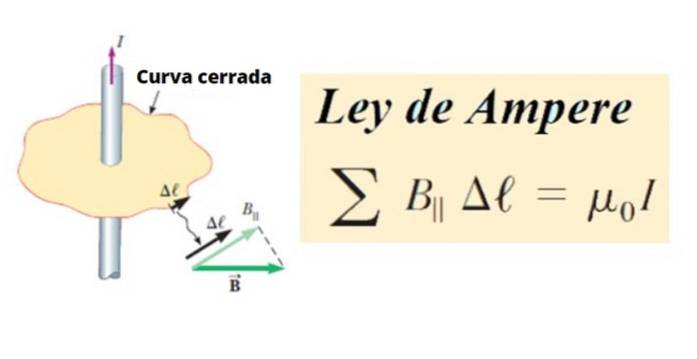
Net als een willekeurige lijn of curve C kan deze worden onderverdeeld in kleine segmenten Δℓ, en deze kunnen op hun beurt oneindig klein zijn, dan worden ze d genoemdℓ.
In dit geval wordt de sommatie een lijnintegraal van het scalaire product tussen de vectoren B. en ds. Dit product bevat de tangentiële component van B, dat is B cosθ, waarbij θ de hoek is tussen de vectoren:
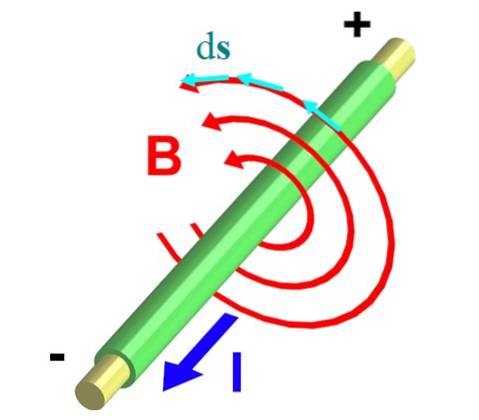
De kleine cirkel door de integraal betekent dat de integratie plaatsvindt over een gesloten pad C, waarbij in dit geval de stroom door de dwarsdoorsnede van de geleider vloeit.
De evenredigheidsconstante die nodig is om gelijkheid vast te stellen, is μof, de doorlaatbaarheid van het vacuüm. Op deze manier is de wet van Ampère:

De wet van Ampère vertelt ons dat de lijnintegraal ∫C B. ∙ ds is precies μofIk, maar het geeft ons niet de details over hoe het magnetische veld is georiënteerd B. met betrekking tot kromme C op elk punt, noch over hoe de integraal moet worden berekend. Het vertelt ons alleen dat het resultaat ervan altijd μ isofik.
Artikel index
- 1 Bewijs van de wet van Ampère
- 1.1 Magnetisch veld van rechtlijnige en oneindige draad
- 2 Opgeloste oefeningen
- 2.1 - Oefening 1
- 2.2 - Oefening 2
- 3 referenties
Demonstratie van de wet van Ampère
De wet van Ampère wordt experimenteel geverifieerd door het magnetische veld te controleren dat wordt geproduceerd door een zeer lange rechtlijnige geleider. Voordat we het probleem aanpakken, moeten we twee gevallen van speciaal belang benadrukken in de vorige vergelijking:
-De eerste is wanneer B. en ds zijn parallel, wat betekent dat B. raakt aan C. Dan is de hoek tussen beide vectoren 0º en is het scalaire product gewoon het product van de grootheden B.ds.
-De tweede treedt op als B. en ds loodrecht staan, in welk geval het scalaire product 0 is, aangezien de hoek tussen de vectoren 90 ° is, waarvan de cosinus 0 is.
Een ander belangrijk detail is de keuze van curve C waarop de veldcirculatie wordt geëvalueerd. De wet van Ampère specificeert niet wat het kan zijn, maar het moet de huidige distributie betreffen. Het zegt ook niet in welke richting de bocht moet worden afgelegd en hiervoor zijn twee mogelijkheden.
De oplossing is om tekens toe te wijzen volgens de regel van de rechterduim. De vier vingers zijn gebogen in de richting waarin u wilt integreren, meestal is dit hetzelfde als het veld B. circuleren. Als de stroom in de richting van de rechterduim wijst, krijgt deze een + -teken en zo niet een teken -.
Dit is van toepassing wanneer er een verdeling is met meerdere stromen, sommige positief en andere negatief. De algebraïsche som daarvan is degene die we gaan plaatsen in de wet van Ampère, die gewoonlijk wordt genoemd als huidige vergrendeld (door curve C).
Oneindig rechtlijnig magnetisch veld van de draad
Figuur 2 toont een draad die een stroom I uit het vlak voert. De regel van de rechterduim zorgt daarvoor B. circuleert tegen de klok in en beschrijft de omtrekken zoals aangegeven door de rode pijlen.

Laten we er een nemen, waarvan de straal r is. We verdelen het in kleine differentiële segmenten ds, vertegenwoordigd door de vectoren in blauw. Beide vectoren, B. en ds, zijn parallel op elk punt van de omtrek, en dus de integraal ∫C B. ∙ ds Het verandert in:
C Bds
Dit komt omdat, zoals we al eerder zeiden, het puntproduct B. ∙ ds is het product van de magnitudes van de vectoren door de cosinus van 0º. We kennen het resultaat van de integraal dankzij de wet van Ampère, daarom schrijven we:
C Bds = μofik
Omdat de grootte van het veld constant is over het hele traject, verlaat het de integraal:
B ∫C ds = μofik
De integraal ∫C ds vertegenwoordigt de som van alle oneindig kleine segmenten die de omtrek van de straal vormen r, gelijk aan zijn lengte, het product van zijn straal met 2π:
B.2πr = μofik
En vanaf daar ontdekken we dat de grootte van B is:
B = μofIk / 2πr
Benadrukt moet worden dat zelfs als het geselecteerde pad (of ampère circuit) was niet circulair, het resultaat van de integraal blijft μofIk echter ∫C B. ∙ ds het zou niet langer zijn B.2πr.
Daarom ligt het nut van de wet van Ampère om het magnetisch veld te bepalen in het kiezen van distributies met hoge symmetrie, zodat de integraal gemakkelijk te evalueren is. Cirkelvormige en rechtlijnige paden voldoen aan deze eis.
Opgeloste oefeningen
- Oefening 1
Beschouw de krommen a, b, c en d in figuur 3. Ze hebben betrekking op drie stromen, waarvan er twee het vlak verlaten, gesymboliseerd door een punt ( . ), waarvan de intensiteiten 1 A en 5 A zijn, en een stroom die het vlak binnenkomt, dat wordt aangegeven met een kruis en waarvan de grootte 2 A is.
Zoek de stroom die door elke curve wordt omsloten.
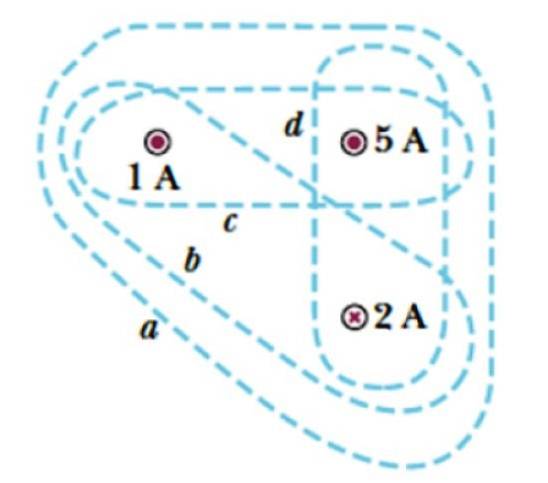
Oplossing
De stromingen die uit het papier komen, krijgen een + -teken. Volgens dit:
Curve a
Het omsluit de drie stromen, daarom is de ingesloten stroom + 1 A + 5 A - 2 A = 4 A.
Curve b
Alleen de stromen van 1 A en -2 A vallen binnen deze curve, daarom is de ingesloten stroom -2 A.
Curve c
Het omsluit de uitgaande stromen 1A en 5 A, daarom is de vergrendelde stroom 6 A.
Curve d
De stromen erin zijn +5 A en -2 A, dus het bevat een netto stroom van 3 A.
- Oefening 2
Bereken de grootte van het magnetische veld dat wordt geproduceerd door een zeer lange rechte draad, op een punt op 1 meter afstand, als de draad een stroom van 1 A voert.
Oplossing
Volgens de wet van Ampère wordt het veld van de draad bepaald door:
B = μofIk / 2πr = (4π x 10-7 x 1 / 2π x 1) T = 2 x 10-7 T.
Referenties
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 6. Elektromagnetisme. Bewerkt door Douglas Figueroa (USB).
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. Ed. Deel 2.
- Serway, R. 2009. College natuurkunde. Cengage leren.
- Tipler, P. (2006) Fysica voor wetenschap en technologie. 5e uitgave Deel 2. Editorial Reverté.

Niemand heeft nog op dit artikel gereageerd.