Blok algebra-elementen, voorbeelden, opgeloste oefeningen

De blok algebra verwijst naar de reeks bewerkingen die via blokken worden uitgevoerd. Deze en enkele andere elementen dienen om een ​​systeem schematisch weer te geven en om de reactie op een gegeven invoer gemakkelijk te visualiseren..

Over het algemeen bevat een systeem verschillende elektrische, elektronische en elektromechanische elementen, en elk ervan, met zijn respectieve functie en positie in het systeem, evenals de manier waarop ze verband houden, wordt geschetst door middel van functionele blokken.

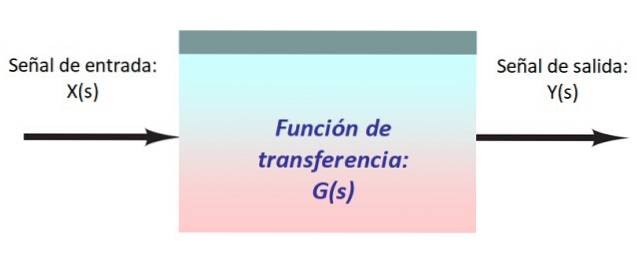
In de bovenstaande figuur is er een heel eenvoudig systeem, bestaande uit een ingangssignaal X (s), dat het blok binnenkomt met de overdrachtsfunctie G (s) die het wijzigt en de uitgang Y (s) produceert.

Het is handig om de signalen en hun pad door het systeem weer te geven door middel van pijlen die elk blok binnenkomen en verlaten. Gewoonlijk wordt de signaalstroom van links naar rechts geleid.

Het voordeel van dit soort schema's is het visuele hulpmiddel dat het biedt bij het begrijpen van het systeem, ook al is het geen fysieke weergave van het systeem. In feite is het blokschema niet uniek, want afhankelijk van het standpunt kunnen zelfs meerdere diagrammen van hetzelfde systeem worden getekend..

Het kan ook gebeuren dat hetzelfde diagram meerdere systemen bedient die niet noodzakelijkerwijs aan elkaar gerelateerd zijn, zolang het hun gedrag maar voldoende beschrijft. Er zijn verschillende systemen waarvan de respons in veel opzichten vergelijkbaar is, bijvoorbeeld een LC-circuit (inductor-condensator) en een massa-veersysteem..

Artikel index

• 1 Wat is een blokschema?
• 2 Elementen van het blokschema
  • 2.1 Het signaal
  • 2.2 Het blok
  • 2.3 Sompunt
  • 2.4 Aftakpunt
• 3 Voorbeelden van blokalgebra-regels
  • 3.1 Trapsgewijze blokken
  • 3.2 Blokken parallel
  • 3.3 Verplaats een opteller naar links
  • 3.4 Verplaats een opteller naar rechts
  • 3.5 Een vertakkingspunt van links naar rechts verplaatsen
  • 3.6 Verplaats een vertakkingspunt van rechts naar links
  • 3.7 Feedbacksysteem
  • 3.8 Systeem met feedback en transducer
• 4 Opgeloste oefeningen
  • 4.1 Oefening 1
  • 4.2 Oefening 2
• 5 referenties

Wat is een blokschema?

De systemen zijn over het algemeen gecompliceerder dan die in figuur 1, maar blokalgebra biedt een reeks eenvoudige regels om het systeemschema te manipuleren en terug te brengen tot de eenvoudigste versie..

Zoals aan het begin uitgelegd, gebruikt het diagram blokken, pijlen en cirkels om de relatie vast te stellen tussen elk onderdeel van het systeem en de stroom van signalen die er doorheen lopen..

Met blokalgebra kunt u twee of meer signalen vergelijken door ze op te tellen, af te trekken en te vermenigvuldigen, en door de bijdrage van elke component aan het systeem te analyseren.

Hierdoor is het mogelijk om het hele systeem terug te brengen tot een enkel ingangssignaal, een enkele overdrachtsfunctie die de werking van het systeem en de bijbehorende uitgang volledig beschrijft..

Blokschema-elementen

De elementen van het blokschema zijn als volgt:

Het signaal

De signalen zijn zeer gevarieerd van aard, het is bijvoorbeeld gebruikelijk dat het een elektrische stroom of een spanning is, maar het kan licht, geluid en meer zijn. Het belangrijkste is dat het informatie over een bepaald systeem bevat.

Het signaal wordt met een hoofdletter aangeduid als het een functie is van de variabele s van de Laplace-transformatie: X (s) (zie figuur 1) of met kleine letters als het een functie van tijd is t, als x (t).

In het blokschema wordt het ingangssignaal weergegeven door een pijl die naar het blok is gericht, terwijl het uitgangssignaal, aangeduid als Y (s) of y (t), wordt aangegeven door een uitgaande pijl.

Zowel de ingangs- als uitgangssignalen zijn uniek en de richting waarin de informatie stroomt wordt bepaald door de richting van de pijl. En de algebra is hetzelfde voor elk van de twee variabelen.

Het blok

Het blok wordt weergegeven door een vierkant of een rechthoek (zie figuur 1) en kan worden gebruikt om bewerkingen uit te voeren of om de overdrachtsfunctie te implementeren, die meestal wordt aangeduid met de hoofdletter G. Deze functie is een wiskundig model dat het antwoord beschrijft. aangeboden door het systeem aan een ingangssignaal.

De overdrachtsfunctie kan worden uitgedrukt in termen van tijd t als G (t) of de variabele s als G (s).

Wanneer het ingangssignaal X (s) het blok bereikt, wordt het vermenigvuldigd met de overdrachtsfunctie en omgezet in het uitgangssignaal Y (s). Wiskundig wordt het als volgt uitgedrukt:

Y (s) = X (s) .G (s)

Op equivalente wijze is de overdrachtsfunctie de verhouding tussen de Laplace-transformatie van het uitgangssignaal en de Laplace-transformatie van het ingangssignaal, op voorwaarde dat de beginvoorwaarden van het systeem nul zijn:

G (s) = Y (s) / X (s)

Som punt

Het toevoegingspunt, of opteller, wordt gesymboliseerd door een cirkel met een kruis erin. Het wordt gebruikt om door middel van optellen en aftrekken twee of meer signalen te combineren. Aan het einde van de pijl die het teken symboliseert, wordt direct een + -teken geplaatst als dat teken wordt toegevoegd of een - -teken als het wordt afgetrokken..

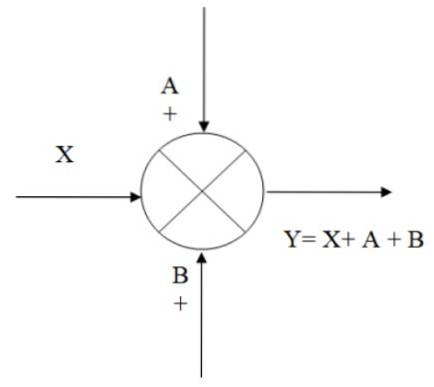
In de volgende afbeelding is er een voorbeeld van hoe de opteller werkt: we hebben het ingangssignaal X, waaraan de signalen A en B worden toegevoegd, waardoor de uitgang Y wordt verkregen, die algebraïsch equivalent is aan:

Y = X + A + B

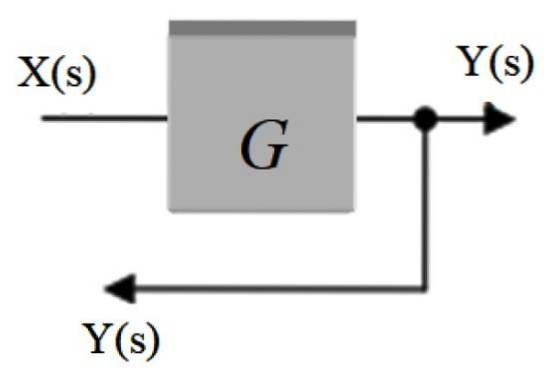
Vertakkingspunt

Het wordt ook wel genoemd splitsingspunt. Daarin wordt het signaal dat uit een blok komt, gedistribueerd naar andere blokken of naar een opteller. Het wordt weergegeven door een punt op de signaalpijl en er komt een andere pijl uit die het signaal naar een ander deel leidt.

Voorbeelden van blokalgebra-regels

Zoals eerder uitgelegd, is het de bedoeling om het systeem uit te drukken met behulp van het blokschema en het te verkleinen om de overdrachtsfunctie te vinden die het beschrijft. Hieronder volgen de blokalgebra-regels om diagrammen te vereenvoudigen:

Trapsgewijze blokken

Als je een signaal hebt dat achtereenvolgens door de G-blokken gaat₁, G_twee, G₃..., wordt teruggebracht tot een enkel blok waarvan de overdrachtsfunctie het product is van G₁, G_twee, G₃​

In het volgende voorbeeld komt het signaal X (s) het eerste blok binnen en is de output:

Y₁(s) = X (s) .G₁(s)

Draai Y₁(s) voer blok G in_twee(s), waarvan de output is:

Y_twee(s) = X (s) .G₁(s). G_twee(s)

De procedure is geldig voor n trapsgewijze blokken:

Y_n (s) = X (s). G₁(s) .G_twee(s) ... G._n(s)

Parallelle blokken

In het diagram aan de linkerkant vertakt het signaal X (s) zich om de G-blokken binnen te gaan₁(s) en G_twee(s):

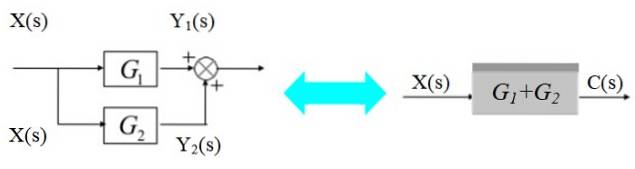
De respectievelijke uitgangssignalen zijn:

Y₁(s) = X (s) .G₁(s)

Y_twee(s) = X (s) .G_twee(s)

Deze signalen worden bij elkaar opgeteld om het volgende te verkrijgen:

C (s) = Y₁(s) + Y_twee(s) = X (s). [G₁(s) + G_twee(s)]

Zoals weergegeven in het diagram aan de rechterkant.

Verplaats een opteller naar links

Een opteller kan als volgt naar links van het blok worden verschoven:

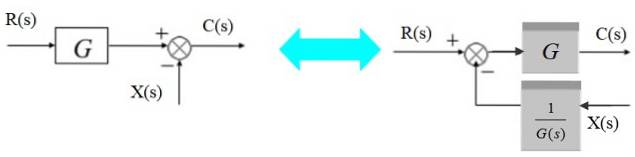
Aan de linkerkant is het uitgangssignaal:

C (s) = R (s). G (s) - X (s)

Equivalent naar rechts:

C (s) = [R (s) - X (s) / G (s)]. G (s)

Verplaats een opteller naar rechts

De opteller kan als volgt naar de rechterkant van het blok worden verplaatst:

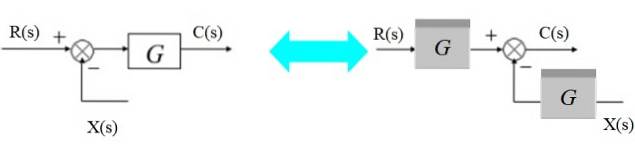
Aan de linkerkant hebben we: [R (s) - X (s)]. G (s) = C (s)

En aan de rechterkant:

R (s). G (s) - X (s). G (s) = C (s)

Verplaats een vertakkingspunt van links naar rechts

Om het vertakkingspunt van links naar rechts van het blok te verplaatsen, moet u er rekening mee houden dat de uitvoer C (s) naar rechts het product X (s) .G (s) is. Omdat je het opnieuw naar X (s) wilt converteren, vermenigvuldig je met het omgekeerde van G (s).

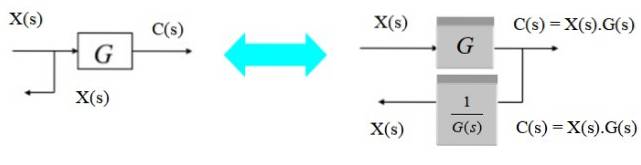
Verplaats een vertakkingspunt van rechts naar links

Als alternatief kan het vertakkingspunt als volgt van rechts naar links worden verschoven:

Aangezien we aan het einde van de tak C (s) willen verkrijgen, voegt u eenvoudig een nieuw blok G (s) in op een vertakking aan de linkerkant van het originele blok.

Feedbacksysteem

In het volgende systeem wordt het uitgangssignaal C (s) teruggekoppeld via de opteller aan de linkerkant:

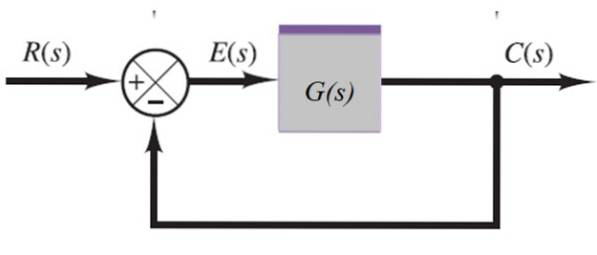
C (s) = E (s) .G (s)

Maar:

E (s) = R (s) -C (s)

Als je deze uitdrukking in de vorige vergelijking vervangt, blijft het: C (s) = [R (s) -C (s)]. G (s), waaruit C (s) kan worden opgelost:

C (s) + C (s) .G (s) = R (s) .G (s) → C (s). [1 + G (s)] = R (s) .G (s)

C (s) = R (s). G (s) / [1 + G (s)]

Of anders:

C (s) / R (s) = G (s) / [1 + G (s)]

In grafische vorm blijft het na vereenvoudiging:

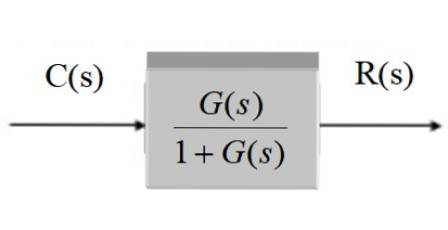
Systeem met feedback en transducer

De transducer bestaat uit de overdrachtsfunctie H (s):

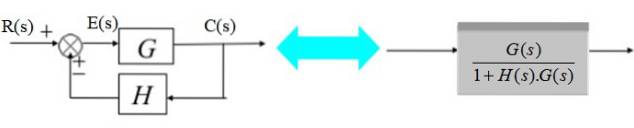
In het diagram rechts is het uitgangssignaal C (s):

C (s) = E (s). G (s) met E (s) = R (s) - C (s). H (s)

Dan:

C (s) = [R (s) - C (s). H (s)]. G (s)

C (s) [1+ H (s) .G (s)] = R (s) .G (s)

Daarom kunnen C (s) worden opgelost door:

C (s) = G (s) .R (s) / [1+ H (s) .G (s)]

En de overdrachtsfunctie zal zijn:

G (s) / [1+ H (s) .G (s)]

Zoals weergegeven in het vereenvoudigde diagram aan de rechterkant.

Opgeloste oefeningen

Oefening 1

Zoek de overdrachtsfunctie van het volgende systeem:

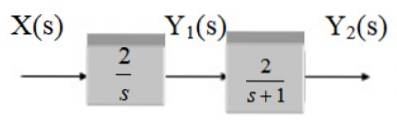
Oplossing

Het behandelt twee blokken in cascade, daarom is de overdrachtsfunctie het product van de functies G₁ en G_twee.

Het moet:

G₁ = 2 / s

G_twee = 2 / (s + 1)

Daarom is de gezochte overdrachtsfunctie:

G (s) = 4 / [s (s + 1)]

Oefening 2

Reduceer het volgende systeem:

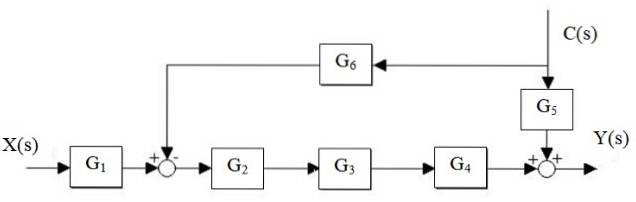
Oplossing

Eerst wordt de G-cascade verminderd_twee, G₃ en G_4, en de parallel G is gescheiden₅ en G₆​

Dan de opteller links van blok G_twee ⋅G₃ ⋅ G₄ beweegt naar rechts:

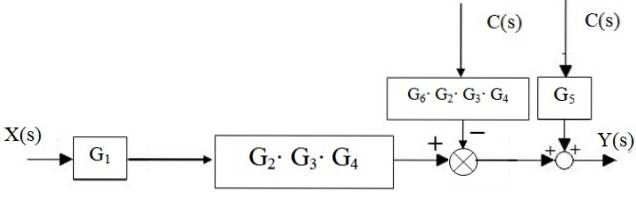
De adders aan de rechterkant zijn teruggebracht tot slechts één, evenals de trapsgewijze blokken:

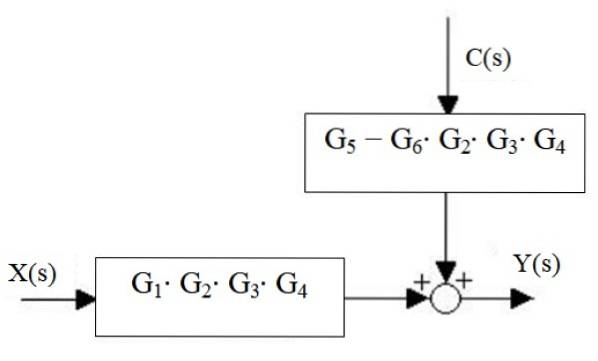
Ten slotte is de output van het systeem:

Y (s) = X (s) ⋅G₁⋅ G_twee ⋅G₃ ⋅ G₄ + C (s) ⋅ [G₅ - G₆ ⋅ G_twee ⋅G₃ ⋅ G₄​

Referenties

1. Alaydi, J. Blokschema besturingssysteem. Hersteld van: site.iugaza.edu.ps.
2. Bolton, W. 2006. Regeltechniek. 2e. Editie. Alpha Omega.
3. Cwalinsky, J. Inleiding tot systeemblokalgebra. Hersteld van: cedengineering.com.
4. Dademuchconnection. Blokken diagram. Hersteld van: dademuch.com.
5. Ogata, K. 2010. Moderne regeltechniek. 5e. Editie. Pearson.