
Orthogonale matrixeigenschappen, bewijs, voorbeelden

Het heeft een orthogonale matrix wanneer genoemde matrix vermenigvuldigd met zijn transponering resulteert in de identiteitsmatrix. Als de inverse van een matrix gelijk is aan de transponering, is de oorspronkelijke matrix orthogonaal.
Orthogonale matrices hebben als kenmerk dat het aantal rijen gelijk is aan het aantal kolommen. De rijvectoren zijn ook orthogonale eenhedenvectoren en de getransponeerde rijvectoren ook.
Wanneer een orthogonale matrix wordt vermenigvuldigd met de vectoren van een vectorruimte, levert dit een op isometrische transformatie, dat wil zeggen, een transformatie die de afstanden niet verandert en de hoeken behoudt.
Een typische vertegenwoordiger van orthogonale matrices zijn de rotatiematrices. De transformaties van orthogonale matrices op een vectorruimte worden genoemd orthogonale transformaties.
De geometrische transformaties van rotatie en reflectie van punten voorgesteld door hun Cartesiaanse vectoren worden uitgevoerd door orthogonale matrices toe te passen op de originele vectoren om de coördinaten van de getransformeerde vectoren te verkrijgen. Het is om deze reden dat orthogonale matrices op grote schaal worden gebruikt bij computationele grafische verwerking..
Artikel index
- 1 Eigenschappen
- 2 Demo
- 3 voorbeelden
- 3.1 Voorbeeld 1
- 3.2 Voorbeeld 2
- 3.3 Voorbeeld 3
- 3.4 Voorbeeld 4
- 4 referenties
Eigendommen
Een array M. is orthogonaal indien vermenigvuldigd met de transponering M.T geeft de identiteitsmatrix terug ik. Evenzo resulteert het product van de transponering van een orthogonale matrix door de originele matrix in de identiteitsmatrix:
M MT = MT M = ik
Als gevolg van de vorige verklaring hebben we dat de transponering van een orthogonale matrix gelijk is aan zijn inverse matrix:
M.T = M-1.
De set orthogonale matrices van de dimensie n x n vormen de groep van orthogonale Aan). En de subset van Aan) van orthogonale matrices met determinant +1 vormen de Groep unitaire speciale matrices SU (n). De groepsmatrices ZO (n) zijn matrices die lineaire rotatietransformaties produceren, ook wel bekend als de rotaties groep.
Demonstratie
Laten we laten zien dat een matrix orthogonaal is als, en alleen als, de rijvectoren (of de kolomvectoren) orthogonaal zijn ten opzichte van elkaar en van norm 1.
Stel dat de rijen van een orthogonale matrix n x n n orthonormale vectoren van dimensie n zijn. Indien aangegeven door v1, vtwee,…., Vn aan de n vectoren is voldaan:
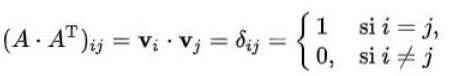
Waar het duidelijk is dat de reeks rijvectoren inderdaad een reeks orthogonale vectoren is met norm één.
Voorbeelden
voorbeeld 1
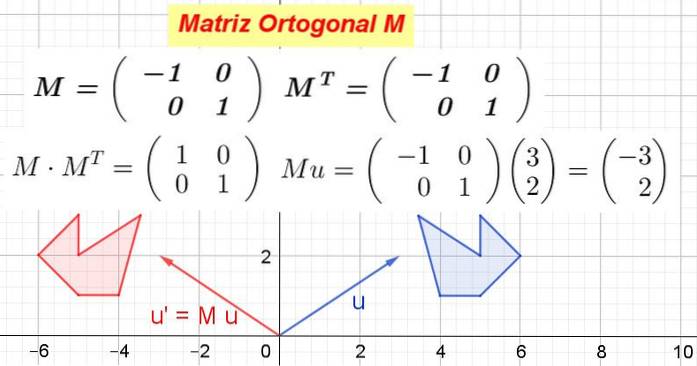
Laat zien dat de 2 x 2 matrix die in de eerste rij de vector heeft v1= (-1 0) en in de tweede rij de vector v2= (0 1) is een orthogonale matrix.
Oplossing: De matrix is gebouwd M. en zijn omzetting wordt berekend M.T
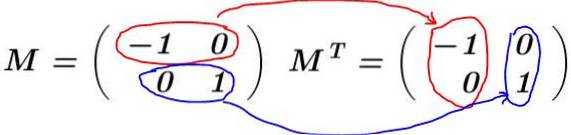
In dit voorbeeld is de array M. het is zelf-getransponeerd, dat wil zeggen, de matrix en zijn getransponeerde zijn identiek. Het vermenigvuldigt zich M. door zijn omzetting M.T
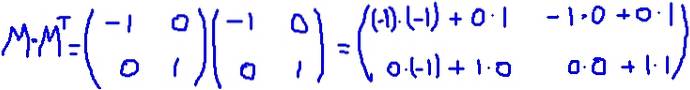
Het is geverifieerd dat M. M.T is gelijk aan de identiteitsmatrix:
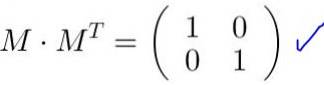
Wanneer de matrix M. wordt vermenigvuldigd met de coördinaten van een vector of een punt, nieuwe coördinaten worden verkregen die overeenkomen met de transformatie die de matrix maakt op de vector of het punt.
Figuur 1 laat zien hoe M. transformeren vector of Aan of' en ook hoe M. transformeer de blauwe veelhoek in de rode veelhoek. Wat M. is orthogonaal het is dan een orthogonale transformatie, die de afstanden en hoeken behoudt.
Voorbeeld 2
Stel dat u een matrix van 2 x 2 hebt gedefinieerd in de reals die worden gegeven door de volgende uitdrukking:
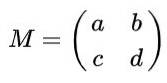
Vind de echte waarden van naar, b, c Y d zodanig dat de matrix M. een orthogonale matrix zijn.
Oplossing: Per definitie is een matrix orthogonaal als vermenigvuldigd met zijn transpositie de identiteitsmatrix wordt verkregen. Onthoud dat de getransponeerde matrix wordt verkregen uit het origineel, waarbij rijen worden verwisseld voor kolommen, en de volgende gelijkheid wordt verkregen:
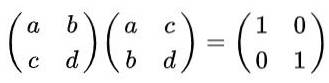
Als we de matrixvermenigvuldiging uitvoeren, hebben we:
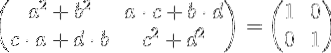
Door de elementen van de linkermatrix gelijk te stellen met de elementen van de identiteitsmatrix aan de rechterkant, krijgen we een stelsel van vier vergelijkingen met vier onbekenden a, b, c en d.
We stellen de volgende uitdrukkingen voor a, b, c en d voor in termen van trigonometrische verhoudingen sinus en cosinus:
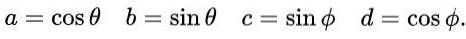
Met dit voorstel en vanwege de fundamentele trigonometrische identiteit, wordt automatisch voldaan aan de eerste en derde vergelijking in de gelijkheid van de matrixelementen. De derde en vierde vergelijking zijn hetzelfde en in matrixgelijkheid na vervanging van de voorgestelde waarden ziet het er als volgt uit:
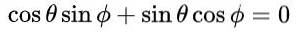
wat leidt tot de volgende oplossing:
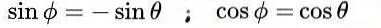
Ten slotte worden de volgende oplossingen verkregen voor de orthogonale matrix M:
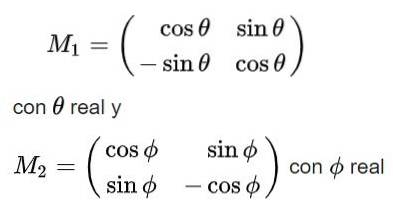
Merk op dat de eerste oplossing determinant +1 heeft en dus tot de groep SU (2) behoort, terwijl de tweede oplossing determinant -1 heeft en daarom niet tot deze groep behoort..
Voorbeeld 3
Gegeven de volgende matrix, zoek de waarden van a en b zodat we een orthogonale matrix hebben.
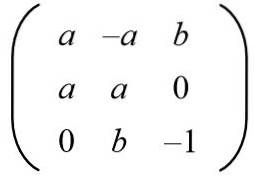
Oplossing: Om een gegeven matrix orthogonaal te laten zijn, moet het product met zijn transpositie de identiteitsmatrix zijn. Vervolgens wordt het matrixproduct van de gegeven matrix met zijn getransponeerde matrix uitgevoerd, wat het volgende resultaat geeft:
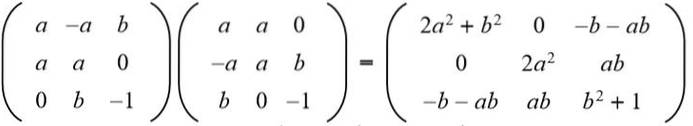
Vervolgens wordt het resultaat gelijkgesteld aan de 3 x 3 identiteitsmatrix:
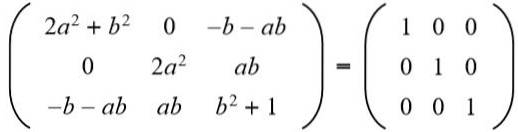
In de tweede rij derde kolom hebben we (een b = 0), maar naar het kan niet nul zijn, want als dat zo is, zou niet aan de gelijkheid van de elementen van de tweede rij en de tweede kolom zijn voldaan. Dan noodzakelijkerwijs b = 0. Vervangen b voor de waarde 0 hebben we:
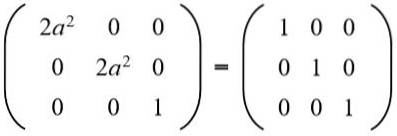
Dan is de vergelijking opgelost: 2a ^ 2 = 1, wiens oplossingen zijn: + ½√2 en -½√2.
De positieve oplossing nemen voor naar de volgende orthogonale matrix wordt verkregen:
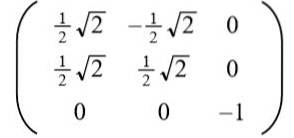
De lezer kan gemakkelijk verifiëren dat de rijvectoren (en ook de kolomvectoren) orthogonaal en unitair zijn, dat wil zeggen orthonormaal.
Voorbeeld 4
Bewijs dat de matrix NAAR wiens rijvectoren zijn v1 = (0, -1 0), v2 = (1, 0, 0) Y v3 = (0 0-1) is een orthogonale matrix. Ontdek ook hoe de vectoren van de canonieke basis worden getransformeerd Ik J K naar vectoren u1, u2 Y u3.
Oplossing: Er moet aan worden herinnerd dat het element (i, j) van een matrix vermenigvuldigd met zijn transponering, het puntproduct is van de vector van rij (i) met die van kolom (j) van de transponering. Bovendien is dit product gelijk aan de Kronecker-delta in het geval dat de matrix orthogonaal is:
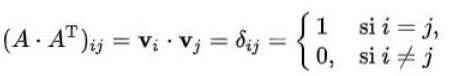
In ons geval ziet het er als volgt uit:
v1 • v1 = 0x0 + (-1) x (-1) + 0x0 = 1
v2 • v2 = 1 × 1 + 0x0 + 0x0 = 1
v3 • v3 = 0x0 + 0x0 + (-1) x (-1) = 1
v1 • v2 = 0x1 + (-1) x0 + 0x0 = 0
v2 • v1 = 1 × 0 + 0x (-1) + 0x0 = 0
v2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0
v3 • v2 = 0x1 + 0x (0) + (-1) x0 = 0
v1 • v3 = 0x0 + (-1) x (0) + 0x (-1) = 0
v3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0
Waarmee wordt aangetoond dat het een orthogonale matrix is.
Bovendien u1 = EEN ik = (0, 1, 0) u2 = EEN j = (-1, 0, 0) en tot slot u3 = Een k = (0, 0, -1)
Referenties
- Anthony Nicolaides (1994) Determinanten en matrices. Pass publicatie.
- Birkhoff en MacLane. (1980). Moderne algebra, ed. Vicens-Vives, Madrid.
- Casteleiro Villalba M. (2004) Inleiding tot lineaire algebra. ESIC-redactie.
- Dave Kirkby (2004) Maths Connect. Heinemann.
- Jenny Olive (1998) Maths: A Student's Survival Guide. Cambridge University Press.
- Richard J. Brown (2012) Wiskunde van 30 seconden: de 50 meest geestverruimende theorieën in de wiskunde. Ivy Press beperkt.
- Wikipedia. Orthogonale matrix. Hersteld van: es.wikipedia.com
- Wikipedia. Orthogonale matrix. Hersteld van: en.wikipedia.com



Niemand heeft nog op dit artikel gereageerd.