
Geschatte meting van amorfe figuren, voorbeeld en oefening
De geschatte meting van amorfe figuren bestaat uit een reeks methoden die worden gebruikt om het gebied of de omtrek van geometrische figuren te bepalen die geen driehoeken, vierkanten, cirkels, enz. zijn. Sommige zijn uitbreidbaar tot driedimensionale figuren.
In wezen bestaat de meting uit het maken van een raster met een regelmatige vorm, zoals rechthoeken, vierkanten of trapeziums, die ongeveer het oppervlak bedekken. De nauwkeurigheid van de oppervlaktebenadering die met deze methoden wordt verkregen, neemt toe met de fijnheid of dichtheid van het rooster..

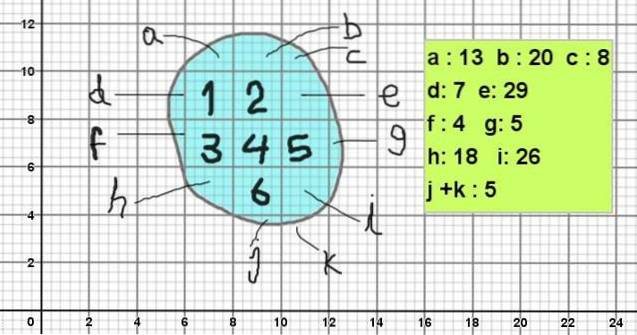
De figuren 1 en 2 tonen verschillende amorfe figuren. Om de oppervlakte te berekenen is een raster gemaakt, bestaande uit 2 x 2 vierkanten, die op hun beurt weer onderverdeeld zijn in vijfentwintig 2/5 x 2/5 vierkanten.
Door de gebieden van de hoofdvierkanten en de secundaire vierkanten toe te voegen, wordt de geschatte oppervlakte van de amorfe figuur verkregen.
Artikel index
- 1 Gebied onder een bocht
- 1.1 Regelmatige intervallen
- 2 Voorbeeld
- 3 Oefening opgelost
- 4 referenties
Gebied onder een bocht
Vaak is het nodig om de oppervlakte onder een curve tussen twee grenswaarden grofweg te berekenen. In dit geval kunnen in plaats van een vierkant rooster rechthoekige strepen worden getekend die ruwweg het gebied onder die curve bedekken..
De som van alle rechthoekige strepen wordt genoemd som of Riemann-som. Figuur 3 toont een verdeling van het interval [a, b] waarover we het gebied onder de curve willen benaderen.
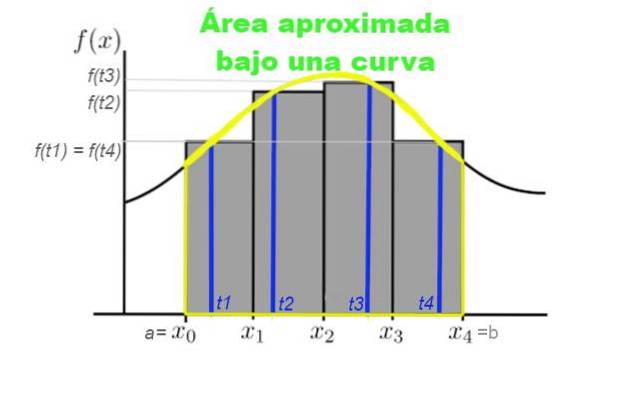
Stel dat u de oppervlakte onder de curve wilt berekenen die wordt gegeven door de functie y = f (x), waarbij x hoort bij het interval [a, b] waarbinnen u de oppervlakte wilt berekenen. Hiervoor wordt binnen dit interval een verdeling van n elementen gemaakt:
Partitie = x0 = a, x1, x2, ..., xn = b.
Vervolgens wordt de geschatte oppervlakte onder de curve gegeven door y = f (x) in het interval [a, b] verkregen door de volgende sommatie uit te voeren:
S = ∑k = 1n f (tk) (xk - Xk-1
Waar Tk is tussen xk-1 en xk: xk-1 ≤ tk ≤ xk .
Figuur 3 toont grafisch de Riemann-som van de kromme y = f (x) in het interval [x0, x4]. In dit geval is er een verdeling van vier subintervallen gemaakt en de som vertegenwoordigt de totale oppervlakte van de grijze rechthoeken.
Deze som vertegenwoordigt een benadering van het oppervlak onder de curve f tussen de abscis x = x0 en x = x4.
De benadering van het gebied onder de curve verbetert naarmate het aantal toeneemt n van partities is groter, en heeft de neiging om precies het gebied onder de curve te zijn wanneer het aantal n van partities neigt naar oneindig.
In het geval dat de curve wordt weergegeven door een analytische functie, worden de waarden f (tk) worden berekend door deze functie te evalueren bij de t-waardenk. Maar als de curve geen analytische uitdrukking heeft, blijven de volgende mogelijkheden over:
- Benader de curve met een functie, bijvoorbeeld een polynoom.
- Neem de cartesische coördinaten van de punten waar de curve de lijnen x = t snijdtk.
Regelmatige intervallen
Afhankelijk van de keuze van de waarde tk in het interval [xk, Xk-1], kan de som de exacte waarde van de oppervlakte onder de curve van de functie y = f (x) overschatten of onderschatten. Het meest aan te raden is om het punt tk te nemen waar het ontbrekende gebied ongeveer gelijk is aan het overtollige gebied, hoewel het niet altijd mogelijk is om een dergelijke keuze te maken..
Neem de tk helemaal rechts
Het meest praktische is dan om regelmatige intervallen met de breedte Δx = (b - a) / n te gebruiken, waarbij a en b de minimum- en maximumwaarden van de abscis zijn, terwijl n het aantal onderverdelingen is.
In dat geval wordt het oppervlak onder de curve benaderd door:
Oppervlakte = f (a + Δx) + f (a + 2Δx) +… + f [a + (n-1] Δx + f (b) * Δx
In de bovenstaande uitdrukking werd tk aan de rechterkant van het subinterval genomen.
Neem de tk helemaal links
Een andere praktische mogelijkheid is om de waarde tk uiterst links te nemen, in welk geval de som die de oppervlakte benadert, wordt uitgedrukt als:
Oppervlakte = [f (a) + f (a + Δx) +… + f (a + (n-1) Δx)] * Δx
Neem tk als centrale waarde
In het geval dat tk wordt gekozen als de centrale waarde van het reguliere subinterval met breedte Δx, is de som die het gebied onder de curve benadert:
Oppervlakte = [f (a + Δx / 2) + f (a + 3Δx / 2) +… + f (b- Δx / 2)] * Δx
Elk van deze uitdrukkingen neigt naar de exacte waarde in die mate dat het aantal onderverdelingen willekeurig groot is, dat wil zeggen dat Δx naar nul neigt, maar in dit geval wordt het aantal termen in de sommatie enorm groot met de daaruit voortvloeiende rekenkosten..
Voorbeeld
Figuur 2 toont een amorfe figuur, waarvan de contour lijkt op de stenen in afbeelding 1. Om de oppervlakte te berekenen, wordt deze op een rooster geplaatst met hoofdvierkanten van 2 x 2 vierkante eenheden (ze kunnen bijvoorbeeld 2 cm² groot zijn)..
En aangezien elk vierkant is onderverdeeld in 5 x 5 onderverdelingen, heeft elke onderverdeling een oppervlakte van 0,4 x 0,4 vierkante eenheden (0,16 cm²).
De oppervlakte van de figuur wordt als volgt berekend:
Oppervlak = 6 x 2 cm² + (13 + 20 + 8 + 7 + 29 + 4 + 5 + 18 + 26 + 5) x 0,16 cm²
Namelijk:
Oppervlakte = 12 cm² + 135 x 0,16 cm² = 33,6 cm².
Oefening opgelost
Bereken ongeveer de oppervlakte onder de curve gegeven door de functie f (x) = xtwee tussen a = -2 tot en met b = +2. Om dit te doen, schrijft u eerst de som voor n reguliere partities van het interval [a, b] en neemt u vervolgens de wiskundige limiet voor het geval dat het aantal partities naar oneindig neigt.
Oplossing
Eerst definieer je het interval van de partities als
Δx = (b - a) / n.
Dan ziet de juiste som die overeenkomt met de functie f (x) er als volgt uit:


[-2 + (4i / n)]twee = 4 - 16 ik / n + (4 / n)twee iktwee
En dan wordt het vervangen in de sommatie:



En de derde resultaten:

S (f, n) = 16 - 64 (n + 1) / 2n + 64 (n + 1) (2n + 1) / 6ntwee
Als u een hoge waarde kiest voor n, krijgt u een goede benadering van het gebied onder de curve. In dit geval is het echter mogelijk om de exacte waarde te krijgen door de wiskundige limiet te nemen wanneer n naar oneindig neigt:
Gebied = limn-> ∞[16 - 64 (n + 1) / 2n + 64 (n + 1) (2n + 1) / 6ntwee
Oppervlakte = 16 - (64/2) + (64/3) = 16/3 = 5.333.
Referenties
- Casteleiro, J. M. 2002. Integrale calculus (geïllustreerde uitgave). Madrid: ESIC-redactie.
- Larson, R. 2010. Berekening van een variabele. 9e. Editie. Mcgraw heuvel.
- Purcell, E. 2007. Calculus met analytische meetkunde. 9e. Editie. Pearson Education.
- Unican. Geschiedenis van het concept integraal. Hersteld van: repositorio.unican.es
- UIS. Riemann sommen. Hersteld van: matematicas.uis.edu.co
- Wikipedia. Oppervlakte. Hersteld van: es.wikipedia.com



Niemand heeft nog op dit artikel gereageerd.