
Koppelkarakteristieken en formules, oefeningen

De koppel, koppel of moment van een kracht is het vermogen van een kracht om een bocht te veroorzaken. Etymologisch krijgt het de naam koppel als een afleiding van het Engelse woord koppel, uit het latijn koppel (twist).
Het koppel (met betrekking tot een bepaald punt) is de fysieke grootte die resulteert uit het maken van het vectorproduct tussen de positievectoren van het punt waar de kracht wordt uitgeoefend en dat van de uitgeoefende kracht (in de aangegeven volgorde). Dit moment hangt af van drie hoofdelementen.
Het eerste van deze elementen is de grootte van de uitgeoefende kracht, het tweede is de afstand tussen het punt waarop het wordt uitgeoefend en het punt waarmee het lichaam roteert (ook wel de hefboomarm genoemd), en het derde element is de hoek van toepassing van genoemde kracht.
Hoe groter de kracht, hoe groter de spin. Hetzelfde gebeurt met de hefboomarm: hoe groter de afstand tussen het punt waarop de kracht wordt uitgeoefend en het punt ten aanzien waarvan deze de draai produceert, hoe groter deze zal zijn..
Het koppel is natuurlijk van bijzonder belang in de bouw en de industrie, en het is ook aanwezig in talloze toepassingen voor thuis, zoals wanneer een moer wordt vastgedraaid met een sleutel..
Artikel index
- 1 Formules
- 1.1 Eenheden
- 2 kenmerken
- 3 Resulterend koppel
- 4 Toepassingen
- 5 oefeningen opgelost
- 5.1 Oefening 1
- 5.2 Oefening 2
- 6 referenties
Formules
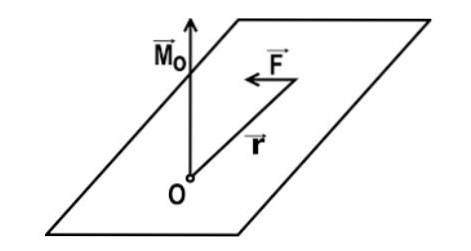
De wiskundige uitdrukking van het koppel van een kracht ten opzichte van een punt O wordt gegeven door: M = r x F
In deze uitdrukking is r de vector die het punt van O verbindt met het punt P waarop de kracht wordt uitgeoefend, en F is de vector van de uitgeoefende kracht.
De meeteenheden van het moment zijn N ∙ m, die, hoewel dimensioneel equivalent aan de Joule (J), een andere betekenis hebben en niet moeten worden verward.
Daarom neemt de modulus van het koppel de waarde aan die wordt gegeven door de volgende uitdrukking:
M = r ∙ F ∙ sin α
In deze uitdrukking is α de hoek tussen de krachtvector en de vector r of hefboomarm. Het koppel wordt als positief beschouwd als het lichaam tegen de klok in draait; integendeel, het is negatief als het met de klok mee draait.
Eenheden
Zoals hierboven reeds vermeld, is de meeteenheid van het koppel het resultaat van het product van een eenheid van kracht en een eenheid van afstand. In het bijzonder gebruikt het internationale systeem van eenheden de newtonmeter waarvan het symbool N • m is.
Op dimensionaal niveau lijkt de newtonmeter misschien gelijk aan de joule; juli mag echter in geen geval worden gebruikt om momenten uit te drukken. De joule is een eenheid voor het meten van werken of energieën die conceptueel sterk verschillen van torsiemomenten..
Op dezelfde manier heeft het torsiemoment een vectorkarakter, dat zowel het scalaire werk als de energie is.
Kenmerken
Uit wat is gezien, volgt dat het koppel van een kracht ten opzichte van een punt het vermogen voorstelt van een kracht of reeks krachten om de rotatie van dat lichaam om een as die door het punt gaat, te wijzigen..
Daarom genereert het torsiemoment een hoekversnelling op het lichaam en is het een grootte van een vectorkarakter (het wordt dus gedefinieerd vanuit een module, een richting en een gevoel) dat aanwezig is in de mechanismen die zijn onderworpen aan torsie of buiging..
Het koppel is nul als de krachtvector en de vector r dezelfde richting hebben, omdat in dat geval de waarde van sin α nul is.
Resulterend koppel
Gegeven een bepaald lichaam waarop een reeks krachten inwerkt, als de uitgeoefende krachten in hetzelfde vlak werken, het koppel dat het resultaat is van de toepassing van al deze krachten; is de som van de torsiemomenten resulterend uit elke kracht. Daarom is het waar dat:
M.T = ∑ M = M1 + M.twee + M.3 +
Het is natuurlijk noodzakelijk om rekening te houden met het tekencriterium voor torsiemomenten, zoals hierboven uitgelegd.
Toepassingen
Het koppel is aanwezig in toepassingen die zo alledaags zijn als het aandraaien van een moer met een sleutel, of het openen of sluiten van een kraan of een deur.
De toepassingen gaan echter veel verder; het koppel zit ook in de assen van de machine of in het resultaat van de inspanningen waaraan de balken worden blootgesteld. Daarom zijn de toepassingen in de industrie en mechanica talrijk en gevarieerd..

Opgeloste oefeningen
Hieronder staan een aantal oefeningen om het bovenstaande beter te begrijpen.
Oefening 1
Gegeven de volgende figuur waarin de afstanden tussen punt O en punten A en B respectievelijk 10 cm en 20 cm zijn:
a) Bereken de waarde van de modulus van het koppel ten opzichte van punt O als een kracht van 20 N wordt uitgeoefend op punt A.
b) Bereken wat de waarde moet zijn van de kracht die in B wordt uitgeoefend om hetzelfde koppel te bereiken als in de vorige paragraaf.
Oplossing
In de eerste plaats is het handig om de gegevens over te dragen naar eenheden van het internationale systeem.
rNAAR = 0,1 m
rB = 0,2 m
a) Om de modulus van het koppel te berekenen, gebruiken we de volgende formule:
M = r ∙ F ∙ sin α = 0,1 ∙ 20 ∙ 1 = 2 N ∙ m
b) Om de gevraagde kracht te bepalen, gaat u op dezelfde manier te werk:
M = r ∙ F ∙ sin α = 0.2 ∙ F ∙ 1 = 2 N ∙ m
Oplossend voor F wordt verkregen dat:
F = 10 N
Oefening 2
Een vrouw oefent een kracht van 20 N uit op het uiteinde van een 30 cm lange sleutel. Als de hoek van de kracht met de sleutelhendel 30 ° is, wat is dan het aanhaalmoment op de moer??
Oplossing
De volgende formule wordt toegepast en de bewerking wordt uitgevoerd:
M = r ∙ F ∙ sin α = 0,3 ∙ 20 ∙ 0,5 = 3 N ∙ m
Referenties
- Moment van kracht. (n.d.). Op Wikipedia. Opgehaald op 14 mei 2018, via es.wikipedia.org.
- Koppel (n.d.). Op Wikipedia. Opgehaald op 14 mei 2018, via en.wikipedia.org.
- Serway, R. A. en Jewett, Jr. J.W. (2003). Fysica voor wetenschappers en ingenieurs. 6e Ed. Brooks Cole.
- Marion, Jerry B. (1996). Klassieke dynamiek van deeltjes en systemen. Barcelona: Ed. Reverté.
- Kleppner, Daniel; Kolenkow, Robert (1973). Een inleiding tot mechanica. McGraw-Hill.




Niemand heeft nog op dit artikel gereageerd.