
Uniforme rechtlijnige bewegingskenmerken, formules, oefeningen
De uniforme lijnbeweging of bij constante snelheid is er een waarbij het deeltje langs een rechte lijn en met constante snelheid beweegt. Op deze manier legt de mobiel gelijke afstanden in gelijke tijden af. Als u bijvoorbeeld in 1 seconde 2 meter aflegt, heeft u na 2 seconden 4 meter afgelegd enzovoort.
Om een nauwkeurige beschrijving van de beweging te maken, of deze nu uniform rechtlijnig is of een andere, is het noodzakelijk om een referentiepunt vast te stellen, ook wel bron, ten opzichte waarvan de mobiel van positie verandert.

Als de beweging geheel in een rechte lijn verloopt, is het ook belangrijk om te weten in welke richting het bewegende lichaam zich aflegt.
Op een horizontale lijn is het mogelijk dat de mobiel naar rechts of naar links gaat. Het onderscheid tussen beide situaties wordt gemaakt door middel van tekens, de gebruikelijke afspraak is de volgende: naar rechts volg ik (+) en naar links teken ik (-).
Wanneer de snelheid constant is, verandert de mobiel niet van richting of van zijn gevoel, en ook de grootte van zijn snelheid blijft ongewijzigd..
Artikel index
- 1 Kenmerken
- 1.1 Afgelegde afstand van de v vs. grafiek t
- 2 Formules en vergelijkingen
- 3 Opgeloste oefeningen
- 3.1 Opgeloste oefening 1
- 3.2 - Opgeloste oefening 2
- 4 Toepassingen
- 5 referenties
Kenmerken
De belangrijkste kenmerken van de uniforme rechtlijnige beweging (MRU) zijn de volgende:
-Uurwerk loopt altijd rechtlijnig.
-Een mobiel met MRU legt in gelijke tijden gelijke afstanden of ruimtes af.
-De snelheid blijft ongewijzigd, zowel in omvang als in richting en zin.
-MRU mist acceleratie (geen verandering in snelheid).
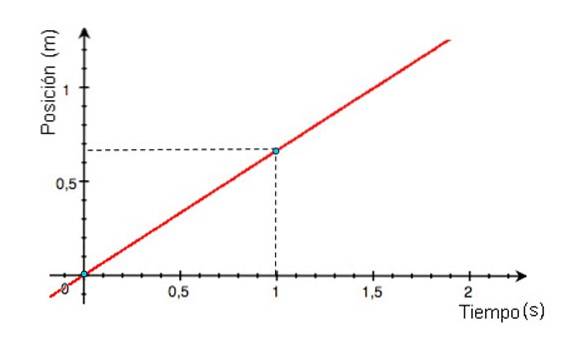
-Omdat de snelheid v blijft constant in de tijd t, de grafiek van zijn grootte als functie van de tijd is een rechte lijn. In het voorbeeld in figuur 2 is de lijn groen gekleurd en wordt de snelheidswaarde afgelezen op de verticale as, ongeveer +0,68 m / s.
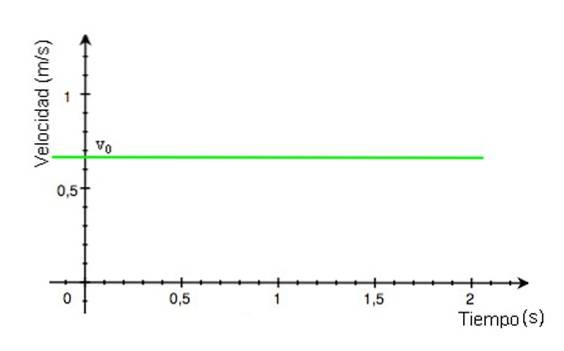
-De grafiek van de positie x ten opzichte van de tijd is een rechte lijn, waarvan de helling gelijk is aan de snelheid van de gsm. Als de lijn van de grafiek x vs t horizontaal is, is de mobiel in rust, als de helling positief is (grafiek van figuur 3), is de snelheid ook positief.
Afgelegde afstand van de v vs. grafiek. t
Ken de afstand die de mobiele telefoon heeft afgelegd wanneer de v vs. grafiek beschikbaar is. t is heel simpel. De afgelegde afstand is gelijk aan het gebied onder de lijn en binnen het gewenste tijdsinterval.
Stel dat u de afstand wilt weten die de gsm in figuur 2 heeft afgelegd in het interval tussen 0,5 en 1,5 seconde.
Dit gebied is dat van de gearceerde rechthoek in figuur 4. Het wordt berekend door het resultaat te vinden van het vermenigvuldigen van de basis van de rechthoek met de hoogte, waarvan de waarden worden afgelezen uit de grafiek.
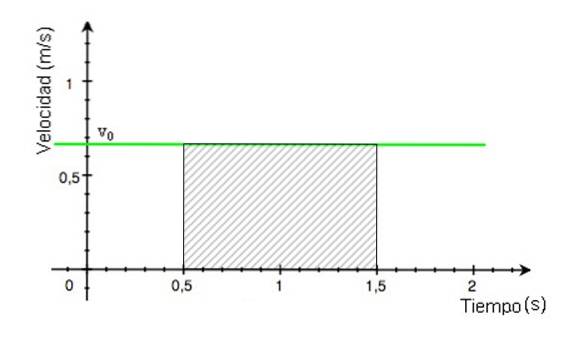
Afgelegde afstand = (1,5 - 0,5) x 0,68 m = 0,68 m
Afstand is altijd een positieve grootheid, ongeacht of deze naar rechts of naar links gaat..
Formules en vergelijkingen
In de MRU zijn de gemiddelde snelheid en de momentane snelheid altijd hetzelfde en aangezien hun waarde de helling is van de grafiek x vs t die overeenkomt met een lijn, zijn de overeenkomstige vergelijkingen als functie van de tijd de volgende:
-Positie als functie van de tijd: x (t) = xof + ww
Xof vertegenwoordigt de uitgangspositie van de gsm, vaak valt het samen met de oorsprong van het referentiesysteem, maar dit is niet altijd het geval. Deze vergelijking is ook bekend als route vergelijking.
-Snelheid als functie van de tijd: v (t) = constant
Als v = 0 betekent dit dat de gsm in rust is. Rust is een bijzonder geval van beweging.
-Versnelling als functie van de tijd: een (t) = 0
Bij uniforme rechtlijnige beweging zijn er geen veranderingen in snelheid, daarom is de versnelling nul.
Opgeloste oefeningen
Zorg er bij het oplossen van een oefening voor dat de situatie overeenkomt met het te gebruiken model. Vooraleer de MRU-vergelijkingen te gebruiken, is het noodzakelijk om ervoor te zorgen dat ze toepasbaar zijn.
De volgende opgeloste oefeningen zijn problemen met twee gsm's.
Opgeloste oefening 1
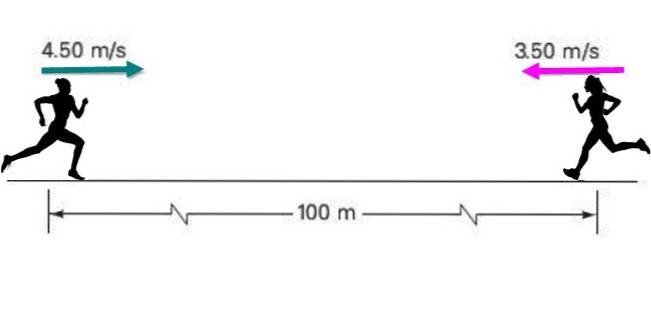
Twee atleten naderen elkaar met een constante snelheid van respectievelijk 4,50 m / s en 3,5 m / s, aanvankelijk gescheiden door een afstand van 100 meter, zoals aangegeven in de figuur.
Als iedereen zijn snelheid constant houdt, zoek dan: a) Hoe lang duurt het voordat ze elkaar ontmoeten? b) Wat zal de positie van elk op dat moment zijn?
Oplossing
Het eerste is om de oorsprong van het coördinatensysteem aan te geven dat als referentie zal dienen. De keuze hangt af van de voorkeur van de persoon die het probleem oplost..
Meestal wordt x = 0 rechts bij het startpunt van de mobiele telefoons gekozen, het kan in de linker of rechter gang zijn, het kan zelfs in het midden van beide worden gekozen.
a) We gaan x = 0 kiezen op de linker loper of loper 1, daarom is de uitgangspositie hiervan x01 = 0 en voor loper 2 is het x02 = 100 m. Loper 1 beweegt van links naar rechts met snelheid v1 = 4,50 m / terwijl loper 2 het van rechts naar links doet met een snelheid van -3,50 m / s.
Bewegingsvergelijking voor de eerste hardloper
X1 = x01 + v1t1 = 4,50t1
Bewegingsvergelijking voor de tweede loper
Xtwee = x02 + vtweettwee = 100-3,50ttwee
Omdat de tijd voor beide hetzelfde is t1 = ttwee = t , wanneer ze elkaar ontmoeten, zal de positie van beide daarom hetzelfde zijn X1 = xtwee. Bij elkaar passen:
4,50t = 100-3,50t
Het is een vergelijking van de eerste graad voor tijd, waarvan de oplossing t = 12,5 s is.
b) Beide lopers bevinden zich in dezelfde positie, daarom vervangt dit de tijd verkregen in de vorige sectie in een van de positievergelijkingen. We kunnen bijvoorbeeld die van makelaar 1 gebruiken:
X1 = 4,50t1 = 56,25 m
Hetzelfde resultaat wordt verkregen door t = 12,5 s in de positievergelijking voor loper 2 te vervangen.
-Oefening opgelost 2
De haas daagt de schildpad uit om een afstand van 2,4 km te lopen en geeft hem om eerlijk te zijn een voorsprong van een half uur. In het spel beweegt de schildpad met een snelheid van 0,25 m / s, wat het maximum is dat hij kan rennen. Na 30 minuten rent de haas met 2 m / s en haalt de schildpad snel in.
Na nog 15 minuten door te hebben gereden, denkt ze dat ze tijd heeft om een dutje te doen en toch de race te winnen, maar valt ze 111 minuten in slaap. Als hij wakker wordt, rent hij uit alle macht, maar de schildpad kwam al over de finish. Vind:
a) Met welk voordeel wint de schildpad?
b) Het moment waarop de haas de schildpad inhaalt
c) Het moment waarop de schildpad de haas inhaalt.
Oplossing voor)
De race begint over t = 0. De positie van de schildpad: XT = 0,25 t
Het haas uurwerk heeft de volgende onderdelen:
-Rust voor het voordeel dat het de schildpad gaf: 0 < t < 30 minutos:
-Race om de schildpad in te halen en blijf een beetje rennen nadat je hem hebt gepasseerd; in totaal zijn er 15 minuten beweging.
-Slaap 111 minuten (rust)
-Word te laat wakkersprint laatste)
2,4 km = 2400 m
De duur van de race was: t = 2400 m / 0,25 m / s = 9600 s = 160 min. Vanaf dit moment nemen we 111 minuten van het dutje en 30 minuten vooruit, dat is 19 minuten (1140 seconden). Het betekent dat je 15 minuten hebt gelopen voordat je ging slapen en 4 minuten nadat je wakker werd voor de sprint.
In deze tijd legde de haas de volgende afstand af:
dL. = 2 m / s. (15. 60 s) + 2 m / s (4. 60 s) = 1800 m + 480 m = 2280 m.
Aangezien de totale afstand 2400 meter was, beide waarden afgetrokken, bleek dat de haas 120 meter verwijderd was van het bereiken van het doel..
Oplossing b)
De positie van de haas voordat hij in slaap valt is XL. = 2 (t - 1800), rekening houdend met de vertraging van 30 minuten = 1800 seconden. Bijpassende xT en xL. we vinden de tijd waarin ze zijn:
2 (t - 1800) 0.25t
2t -0,25 t = 3600
t = 2057,14 s = 34,29 min
Oplossing c)
Tegen de tijd dat de haas wordt ingehaald door de schildpad, slaapt hij 1800 meter vanaf de start:
1800 = 0,25 t
t = 7200 s = 120 min
Toepassingen
De MRU is de eenvoudigste beweging die je je kunt voorstellen en daarom is het de eerste die in de kinematica wordt bestudeerd, maar veel complexe bewegingen kunnen worden beschreven als een combinatie van deze en andere eenvoudige bewegingen..
Als een persoon zijn huis verlaat en rijdt totdat hij een lange rechte snelweg bereikt waarlangs hij lange tijd met dezelfde snelheid reist, kan zijn beweging globaal worden omschreven als een MRU, zonder in detail te treden..
Natuurlijk moet de persoon een paar bochten nemen voordat hij de snelweg op- en afrijdt, maar door dit bewegingsmodel te gebruiken, kan de duur van de reis worden geschat door de geschatte afstand tussen het startpunt en het aankomstpunt te kennen..
In de natuur heeft licht een uniforme rechtlijnige beweging met een snelheid van 300.000 km / s. Evenzo kan in veel toepassingen worden aangenomen dat de beweging van geluid in lucht gelijkmatig rechtlijnig is met een snelheid van 340 m / s..
Bij het analyseren van andere problemen, bijvoorbeeld de beweging van ladingsdragers binnen een geleiderdraad, kan de MRU-benadering ook worden gebruikt om een idee te geven van wat er in de geleider gebeurt..
Referenties
- Bauer, W. 2011. Physics for Engineering and Sciences. Deel 1. Mc Graw Hill, 40-45.
- Figueroa, D. Physics Series for Sciences and Engineering. Deel 3e. Editie. Kinematica. 69-85.
- Giancoli, D. Physics: principes met toepassingen. 6th. Ed Prentice Hall. 19-36.
- Hewitt, Paul. 2012. Conceptuele fysische wetenschappen. 5th. Ed Pearson. 14-18.
- Kirkpatrick, L. 2007. Natuurkunde: een blik op de wereld. 6ta Verkorte editie. Cengage leren. 15-19.
- Wilson, J. 2011. Physics 10. Pearson Education. 116-119.



Niemand heeft nog op dit artikel gereageerd.