
Dubbele bemonstering


Wat is dubbele bemonstering?
De dubbele bemonstering is een techniek die wordt gebruikt in inferentiële statistieken wanneer u meer details en zekerheid wilt weten over een bepaalde variabele, die een bepaalde populatie kenmerkt.
De tweede steekproef van de populatie wordt over het algemeen uitgevoerd nadat een eerste steekproef is genomen en geanalyseerd, waarvan de analyse geen statistisch significante conclusie heeft opgeleverd over een van de studievariabelen..
Om deze reden wordt dubbele steekproeven in Statistieken ook wel bemonstering in twee fasen. Het nut van het tweede monster is dat het helpt om de schatting van verhoudingen en regressies van een bepaalde hulpvariabele, die ontstaat in het licht van de analyse van een eerste monster, nauwkeuriger te bepalen..
Een andere manier waarop dubbele bemonstering wordt gebruikt, is het verzamelen van informatie om een bemonstering per strata uit te voeren..
Voorbeelden
Hieronder worden verschillende situaties beschreven waarin dubbele bemonstering gerechtvaardigd is..
Kwaliteitscontrole bij de productie van onderdelen
De dubbele bemonsteringsmethode wordt vaak gebruikt bij industriële kwaliteitscontrole en verloopt meestal in twee fasen..
Stel bijvoorbeeld een industriële machine die bepaalde onderdelen maakt. Ongeacht hoeveel de machine is afgesteld, geen enkel onderdeel is identiek aan een ander, aangezien er kleine variaties kunnen optreden in de afmetingen en het gewicht. Het gaat erom te bepalen of een partij onderdelen die door de genoemde machine is vervaardigd, voldoet aan de tolerantiecriteria om te worden geaccepteerd of afgekeurd..
Eerst wordt een willekeurige steekproef van stukken genomen waarmee u wilt controleren of een van de variabelen, bijvoorbeeld de lengte van het stuk, binnen de tolerantie valt..
In het geval dat de gemiddelde lengte in dit eerste monster onder of boven de tolerantiegraad ligt die voor de genoemde variabele gewenst is, wordt hieruit afgeleid dat de partij defect is en moet deze worden weggegooid. In dit geval zijn geen nieuwe monsters nodig.
Omgekeerd, als de gemiddelde waarde binnen het tolerantiebereik valt, maar de standaarddeviatie van het monster groot genoeg is om het optellen of aftrekken van de gemiddelde waarde buiten het bereik te laten vallen, dan zal een tweede, grotere steekproef moeten worden verzameld..
Deze tweede steekproef moet de originele steekproef bevatten om de berekeningen opnieuw uit te voeren en zo een definitieve beslissing te kunnen nemen over de onderzochte variabele. Op deze manier kan bekend worden of de batch defect is of niet.
Lagere bemonsteringskosten
Vaak is de informatie over een van de te bestuderen variabelen moeilijk toegankelijk. Maar er kan gemakkelijker een hulpvariabele zijn voor het verzamelen van gegevens.
In dit geval worden twee steekproeven genomen, een grote voor de hulpvariabele, minder duur, en een kleinere steekproef, opgenomen in de grotere steekproef van de duurste variabele..
Deze methode is van toepassing wanneer wordt vastgesteld dat er een correlatie bestaat tussen beide variabelen, die over het algemeen een evenredige relatie is..
Een voorbeeld van deze situatie doet zich voor in de boswetenschappen, waar het gewenst is om het percentage bomen te bepalen dat wordt aangetast door een parasitaire plant (ringworm).
Aangezien dit zeer uitgestrekte gebieden zijn en moeilijk toegankelijk, is het bestuderen van de volledige populatie bomen niet haalbaar in tijd en kosten. Deze stappen worden vervolgens gevolgd:
Stap 1: Monsters nemen
Een voorlopige bemonstering zou bestaan uit het gebruik van luchtfotografie en het bos wordt onderverdeeld in percelen. Van hieruit worden willekeurig een paar percelen gekozen en door analyse van de afbeeldingen van de gekozen percelen wordt geschat hoeveel bomen worden aangetast door ringworm, aangezien de kleur van de bomen wordt beïnvloed door de parasiet..
Stap 2: veldwerk
Maar de fotografische analyse kan onnauwkeurig zijn, dus een paar batches van het eerste monster worden gekozen, bij voorkeur willekeurig, om veldwerk te doen..
Stap 3: vergelijking
Het veldresultaat wordt vervolgens vergeleken met het fotografische resultaat voor het onderscheppen van de twee sets batches. Deze vergelijking kan bijvoorbeeld worden gemaakt door een grafiek te maken waarin de horizontale as de waarde is die voor elke batch door fotografie is verkregen en op de verticale as de waarde die per batch is verkregen door veldwerk..
Deze grafische methode maakt het mogelijk om visueel te identificeren of er al dan niet een correlatie is tussen beide resultaten en om, door middel van een regressieanalyse, de evenredigheidscoëfficiënt of de verhouding tussen beide monsters te bepalen..
Na het grootste monster, dat wil zeggen het fotografische monster, wordt de gemiddelde waarde van geïnfecteerde bomen en hun standaarddeviatie genomen. Maar aangezien de evenredigheidscoëfficiënt en zijn fout met de veldmonsters werden bepaald, is het mogelijk om het resultaat van de grotere steekproef (de fotografische) te corrigeren.
Dit resultaat kan vervolgens worden geëxtrapoleerd naar de gehele boompopulatie.
Voor- en nadelen van dubbele bemonstering
In de beschreven voorbeelden is het kostenvoordeel duidelijk, aangezien het vervangen van een gemakkelijk toegankelijke variabele door een moeilijk toegankelijke variabele tijd en geld bespaart..
Een nadeel is dat bij dubbele bemonstering voor kwaliteitscontrole het risico bestaat dat goede partijen producten buiten tolerantie gaan..
Oefening
We willen het aantal zieke bomen in een bos van 162 hectare schatten. Omdat het bos erg uitgestrekt is, is het onderverdeeld in 100 percelen van hetzelfde gebied. 18 percelen worden willekeurig gekozen en door middel van een fotografisch onderzoek wordt geschat dat er in deze 18 percelen 8,5 zieke bomen zijn met een standaardfout van plus of min 4,5 bomen.
Uit deze 18 plots worden willekeurig 8 plots gekozen waarin het veldonderzoek wordt uitgevoerd. Voor deze acht percelen toont de fotografische studie 10 zieke bomen met een fout van plus of min 5,3 bomen..
Aan de andere kant laat de veldstudie voor diezelfde acht plots 12,4 zieke bomen zien met een fout van plus minus 6,3 bomen.
Het vraagt:
- a) Bepaal de evenredigheidscoëfficiënt tussen het veldonderzoek door middel van lineaire regressie.
- b) Schat het aantal zieke bomen met behulp van de fotografische methode in de honderd percelen.
- c) Pas de correctie toe met de verkregen evenredigheidscoëfficiënt om het werkelijke aantal zieke bomen in het hele bos te schatten.
Oplossing
Er wordt een grafiek gemaakt van het aantal bomen per fotografische telling versus veldtelling voor de acht loten die voor beide onderzoeken zijn geselecteerd..
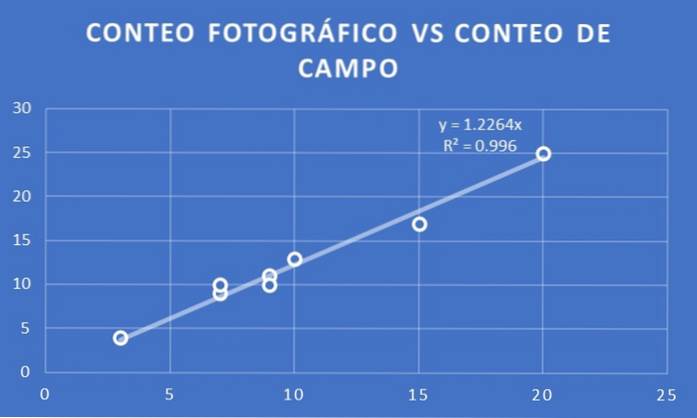
Er wordt een trendlijn aangebracht en de helling bepaald. In dit geval wordt verkregen dat de evenredigheidscoëfficiënt 1,23 is. Dat wil zeggen, als X het aantal per fotografische telling is, wordt geschat dat de veldtelling Y = 1,23 X is.
Het aantal zieke bomen volgens het aantal foto's in de 18 geselecteerde percelen is:
18 x 8,5 = 153
Maar aangezien het hele bos was verdeeld in 100 percelen van hetzelfde gebied, is het aantal zieke bomen geschat door de fotografische methode: (100/18) x 153 = 850.
De correctiefactor verkregen uit de vergelijking tussen veld- en fotografisch onderzoek wordt nu toegepast:
Geschat werkelijk aantal zieke bomen in het bos = 1,23 x 850 = 1046.
Referenties
- Double Sampling for Ratio Estimation, PennState College. Hersteld van psu.edu
- Dubbele, meervoudige en opeenvolgende bemonstering, NC State University. Opgehaald van ncsu.edu
- Eenvoudige willekeurige bemonstering. Opgehaald van investopedia.com
- Wat is dubbele bemonstering? Hersteld van: nist.gov
- Bemonstering. Hersteld van: en.wikipedia.org
- Meertraps bemonstering. Hersteld van: en.wikipedia.org



Niemand heeft nog op dit artikel gereageerd.