De samengestelde nummers zijn die gehele getallen met meer dan twee delers. Als we goed kijken, zijn alle getallen op zijn minst precies deelbaar door zichzelf en door 1. Degenen die alleen deze twee delers hebben, worden priemgetallen genoemd, en degenen die meer hebben, zijn verbindingen..
Laten we eens kijken naar het getal 2, dat alleen kan worden verdeeld tussen 1 en 2. Het getal 3 heeft ook twee delers: 1 en 3. Daarom zijn ze beide priemgetallen. Laten we nu kijken naar het getal 12, dat we precies kunnen delen door 2, 3, 4, 6 en 12. Door 5 delers te hebben, is 12 een samengesteld getal.
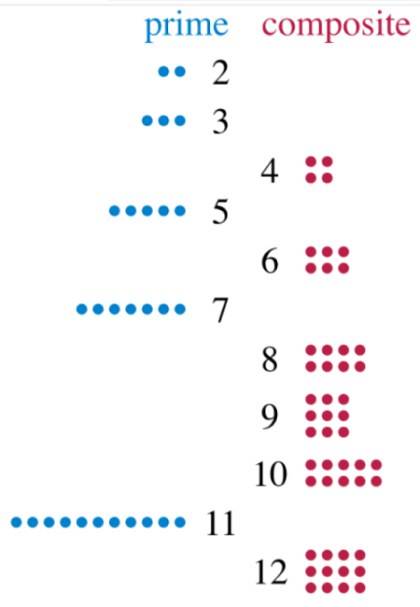
En wat gebeurt er met nummer 1, degene die alle andere verdeelt? Welnu, het is geen priemgetal, omdat het geen twee delers heeft, en het is niet samengesteld, daarom valt 1 niet in een van deze twee categorieën. Maar er zijn veel, veel meer nummers die dat wel doen..
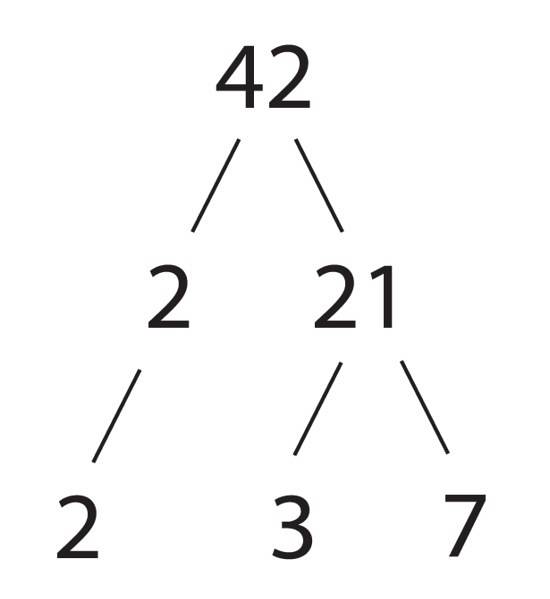
Samengestelde getallen kunnen worden uitgedrukt als het product van priemgetallen, en dit product is, behalve de volgorde van de factoren, uniek voor elk getal. Dit wordt verzekerd door de fundamentele rekenkunde, bewezen door de Griekse wiskundige Euclides (325-365 v.Chr.).
Laten we teruggaan naar nummer 12, dat we op verschillende manieren kunnen uitdrukken. Laten we wat proberen:
12 = 4 x 3 = 2 x 6 = 12 x 1 = 2twee x 3 = 3 x 2twee = 3 x 2 x 2 = 2 x 2 x 3 = 2 x 3 x 2
De vormen die vetgedrukt zijn, zijn producten van priemgetallen en het enige dat verandert, is de volgorde van de factoren, waarvan we weten dat dit het product niet verandert. De andere vormen, hoewel geldig om 12 uit te drukken, bestaan niet alleen uit priemgetallen.
Als we een samengesteld getal willen ontleden in zijn priemfactoren, moeten we het zodanig over priemgetallen verdelen dat de deling exact is, dat wil zeggen dat de rest 0 is.
Deze procedure wordt genoemd ontbinding in priemfactoren of canonieke ontleding. Priemfactoren kunnen worden verhoogd tot positieve exponenten.
We gaan het getal 570 ontleden, waarbij we opmerken dat het even is en daarom deelbaar door 2, wat een priemgetal is.
We gebruiken een schuine streep om het nummer aan de linkerkant te scheiden van de verdelers aan de rechterkant. De respectievelijke quotiënten worden onder het nummer geplaatst wanneer ze worden verkregen. De ontleding is voltooid als het laatste cijfer in de linkerkolom 1 is:
570 │2
285 │
Bij delen door 2 is het quotiënt 285 dat deelbaar is door 5, een ander priemgetal dat eindigt op 5.
570 │2
285 5
57 │
57 is deelbaar door 3, ook een priemgetal, aangezien de som van de cijfers 5 + 7 = 12 een veelvoud is van 3.
570 │2
285 5
57 3
19 │
Ten slotte krijgen we 19, wat een priemgetal is, waarvan de delers 19 en 1 zijn:
570 │2
285 5
57 3
19-19
1 │
Door 1 te verkrijgen, kunnen we 570 al op deze manier uitdrukken:
570 = 2 x 5 x 3 x 19
En we zien dat het in feite het product is van 4 priemgetallen.
In dit voorbeeld beginnen we met delen door 2, maar dezelfde factoren (in een andere volgorde) zouden verkregen zijn als we begonnen met bijvoorbeeld delen door 5.
Om een samengesteld getal in zijn priemfactoren te ontleden, is het nodig om het exact te delen. De criteria voor deelbaarheid tussen priemgetallen zijn regels die het mogelijk maken te weten wanneer een getal precies deelbaar is door een ander getal, zonder te hoeven proberen of bewijzen.
Alle even getallen, die eindigen op 0 of een even getal, zijn deelbaar door 2.
Als de som van de cijfers van een getal een veelvoud is van 3, dan is het getal ook deelbaar door 3.
Getallen die eindigen op 0 of 5 zijn deelbaar door 5.
Een getal is deelbaar door 7 als bij het scheiden van het laatste cijfer, het wordt vermenigvuldigd met 2 en het resterende getal wordt afgetrokken, de resulterende waarde een veelvoud is van 7.
Deze regel lijkt wat ingewikkelder dan de vorige, maar in werkelijkheid is het niet zo veel, dus laten we eens kijken naar een voorbeeld: zal 98 deelbaar zijn door 7?
Laten we de instructies volgen: we scheiden het laatste cijfer, dat 8 is, we vermenigvuldigen het met 2, wat 16 oplevert. Het getal dat overblijft bij het scheiden van de 8 is 9. We trekken 16 - 9 = 7 af. En aangezien 7 een veelvoud van zichzelf is , 98 is deelbaar tussen 7.
Als de som van de cijfers in de even positie (2, 4, 6 ...) wordt afgetrokken van de som van de cijfers in de oneven positie (1, 3, 5, 7 ...) en 0 of een veelvoud van 11 wordt verkregen, wordt het aantal is deelbaar door 11.
De eerste veelvouden van 11 zijn gemakkelijk te herkennen: ze zijn 11, 22, 33, 44 ... 99. Maar wees voorzichtig, 111 is dat niet, in plaats daarvan is 110.
Laten we als voorbeeld eens kijken of 143 een veelvoud van 11 is.
Dit nummer heeft 3 cijfers, het enige even cijfer is 4 (het tweede), de twee oneven cijfers zijn 1 en 3 (eerste en derde), en hun som is 4.
Beide sommen worden afgetrokken: 4 - 4 = 0 en aangezien 0 wordt verkregen, blijkt dat 143 een veelvoud is van 11.
Het getal zonder het enencijfer moet worden afgetrokken van 9 keer dat cijfer. Als de telling 0 of een veelvoud van 13 retourneert, is het getal een veelvoud van 13.
Als voorbeeld zullen we verifiëren dat 156 een veelvoud is van 13. Het enencijfer is 6 en het getal dat buiten blijft is 15. We vermenigvuldigen 6 x 9 = 54 en nu trekken we 54 - 15 = 39 af.
Maar 39 is 3 x 13, dus 56 is een veelvoud van 13.
Twee of meer priemgetallen of samengestelde getallen kunnen priemgetallen of co-priemgetallen zijn. Dit betekent dat de enige gemene deler die ze hebben 1 is.
Er zijn twee belangrijke eigenschappen die u moet onthouden als het gaat om coprimes:
-Twee, drie en meer opeenvolgende getallen zijn altijd een priemgetal naast elkaar.
-Hetzelfde kan gezegd worden voor twee, drie of meer opeenvolgende oneven nummers.
15, 16 en 17 zijn bijvoorbeeld priemgetallen voor elkaar en dat geldt ook voor 15, 17 en 19.
Een priemgetal heeft twee delers, hetzelfde getal en 1. En hoeveel delers heeft een samengesteld getal? Dit kunnen neven en nichten zijn.
Laat N een samengesteld getal zijn, uitgedrukt in termen van zijn canonieke ontleding als volgt:
N = eenn . bm. cp... rk
Waar a, b, c… r de priemfactoren zijn en n, m, p… k de respectievelijke exponenten. Welnu, het aantal delers C dat N heeft, wordt gegeven door:
C = (n +1) (m + 1) (p +1)… (k + 1)
Met C = prime delers + samengestelde delers + 1
Bijvoorbeeld 570, die als volgt wordt uitgedrukt:
570 = 2 x 5 x 3 x 19
Alle priemfactoren worden verhoogd tot 1, daarom heeft 570:
C = (1 + 1) (1 + 1) (1+ 1) (1 +1) = 16 delers
Van deze 10 delers kennen we al: 1, 2, 3, 5, 19 en 570. Er ontbreken nog 10 delers, dit zijn samengestelde getallen: 6, 10, 15, 30, 38, 57, 95, 114, 190 en 285. Ze worden gevonden door de ontbinding in primaire factoren te observeren en ook combinaties van deze factoren met elkaar te vermenigvuldigen..
Ontbind de volgende getallen in priemfactoren:
a) 98
b) 143
c) 540
d) 3705
98 │2
49 │7
7 │7
1 │
98 = 2 x 7 x 7
143 11
13-13
1 │
143 = 11 x 13
540 │5
108 │2
54 │2
27 │3
9 │3
3 │3
1 │
540 = 5 x 2 x 2 x 3 x 3 x 3 = 5 x 2twee x 33
3705 5
741 │3
247 13
19-19
1 │
3705 = 5 x 3 x 13 x 19
Zoek uit of de volgende getallen een priemgetal voor elkaar zijn:
6, 14, 9
-De delers van 6 zijn: 1, 2, 3, 6
-Wat betreft de 14, deze is deelbaar door: 1, 2, 7, 14
-Ten slotte heeft 9 als delers: 1, 3, 9
De enige gemeenschappelijke deler is 1, daarom zijn ze een priemgetal voor elkaar.
Niemand heeft nog op dit artikel gereageerd.