Hyperbolische paraboloïde definitie, eigenschappen en voorbeelden

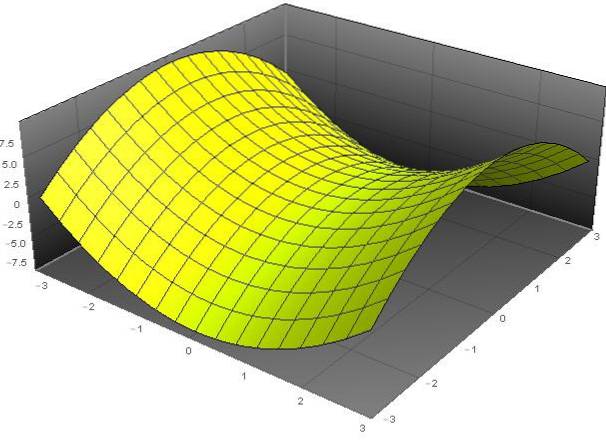
EEN hyperbolische paraboloïde is een oppervlak waarvan de algemene vergelijking in cartesiaanse coördinaten (x, y, z) aan de volgende vergelijking voldoet:

(voor)^twee - (en B)^twee - z = 0.

De naam "paraboloïde" komt van het feit dat de variabele z afhangt van de kwadraten van de variabelen x en y. Terwijl het adjectief "hyperbolisch" te wijten is aan het feit dat we bij vaste waarden van z de vergelijking hebben van een hyperbool. De vorm van dit oppervlak is vergelijkbaar met die van een paardenzadel.

Artikel index

• 1 Beschrijving van de hyperbolische paraboloïde
• 2 Eigenschappen van de hyperbolische paraboloïde
• 3 uitgewerkte voorbeelden
  • 3.1 - Voorbeeld 1
  • 3.2 - Voorbeeld 2
  • 3.3 - Voorbeeld 3
• 4 De hyperbolische paraboloïde in de architectuur
• 5 referenties

Beschrijving van de hyperbolische paraboloïde

Om de aard van de hyperbolische paraboloïde te begrijpen, zal de volgende analyse worden gemaakt:

1.- We nemen het specifieke geval a = 1, b = 1, dat wil zeggen dat de cartesiaanse vergelijking van de paraboloïde blijft als z = x^twee - Y^twee.

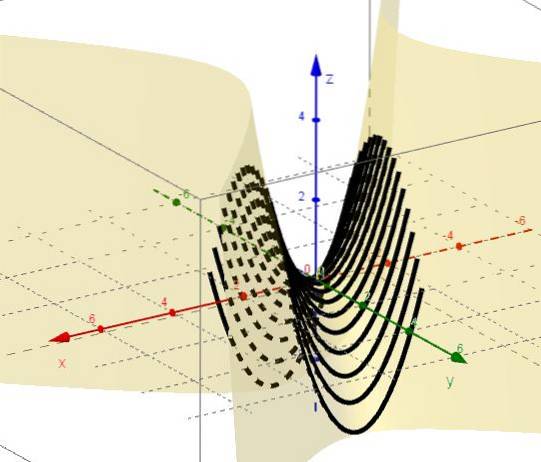
2. - Er wordt rekening gehouden met vlakken parallel aan het ZX-vlak, dat wil zeggen y = ctte.

3. - Met y = ctte blijft z = x^twee - C, die parabolen vertegenwoordigen met takken omhoog en vertex onder het XY-vlak.

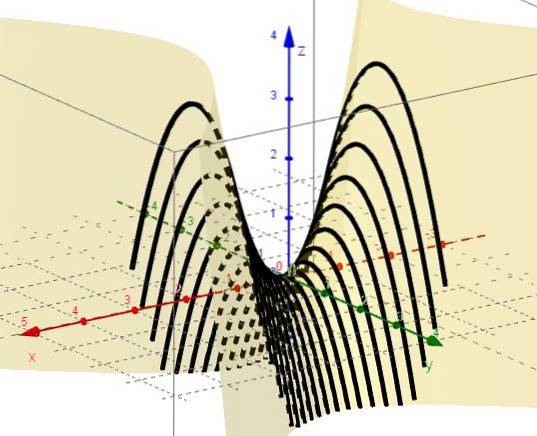
4. - Met x = ctte blijft z = C - y^twee, die parabolen vertegenwoordigen met takken naar beneden en hoekpunt boven het XY-vlak.

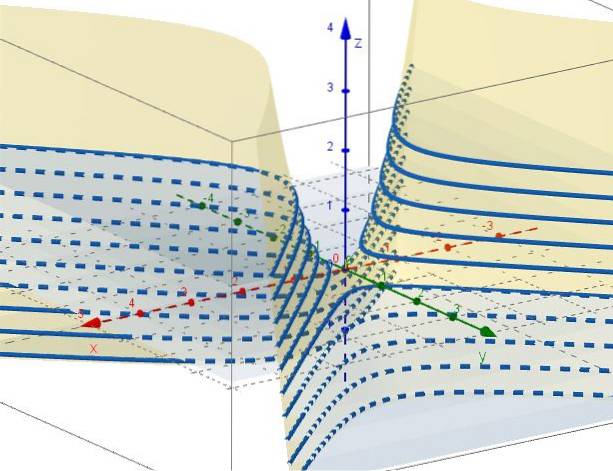
5. - Met z = ctte blijft het C = x^twee - Y^twee, die hyperbolen vertegenwoordigen in vlakken parallel aan het XY-vlak. Als C = 0 zijn er twee lijnen (op + 45º en -45º ten opzichte van de X-as) die elkaar snijden bij de oorsprong op het XY-vlak.

Eigenschappen van de hyperbolische paraboloïde

1.- Vier verschillende punten in de driedimensionale ruimte definiëren één en slechts één hyperbolische paraboloïde.

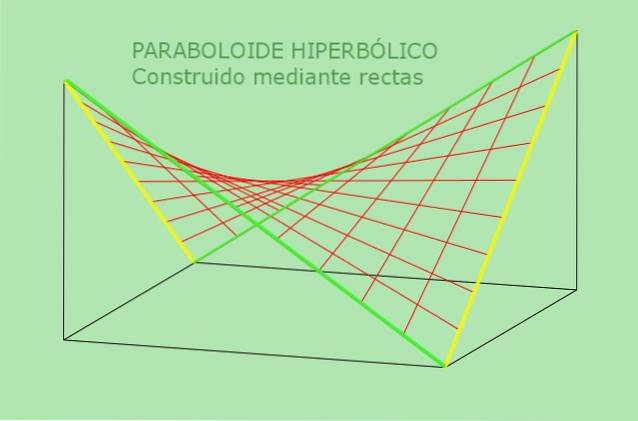
2.- De hyperbolische paraboloïde is een dubbel geregeerd oppervlak. Dit betekent dat ondanks dat het een gekromd oppervlak is, twee verschillende lijnen door elk punt van een hyperbolische paraboloïde gaan die volledig tot de hyperbolische paraboloïde behoren. Het andere oppervlak dat geen vlak is en dubbel wordt geregeerd, is de hyperboloïde van revolutie.

Het is precies de tweede eigenschap van de hyperbolische paraboloïde die zijn brede toepassing in de architectuur mogelijk heeft gemaakt, aangezien het oppervlak kan worden gegenereerd uit balken of rechte touwen..

De tweede eigenschap van de hyperbolische paraboloïde maakt een alternatieve definitie ervan mogelijk: is het oppervlak dat kan worden gegenereerd door een bewegende rechte lijn parallel aan een vast vlak en snijdt twee vaste lijnen die als geleider dienen. De volgende afbeelding verduidelijkt deze alternatieve definitie van de hyperbolische paraboloïde:

Uitgewerkte voorbeelden

- voorbeeld 1

Laat zien dat de vergelijking: z = xy, komt overeen met een hyperbolische paraboloïde.

Oplossing

Er wordt een transformatie toegepast op de variabelen x en y die overeenkomen met een rotatie van de Cartesiaanse assen ten opzichte van de Z-as van + 45º. De oude x- en y-coördinaten worden getransformeerd naar de nieuwe x 'en y' volgens de volgende relaties:

x = x '- y'

y = x '+ y'

terwijl de z-coördinaat hetzelfde blijft, dat wil zeggen, z = z '.

Door in de vergelijking z = x te substitueren, hebben we:

z '= (x' - y ') (x' + y ')

Door het opmerkelijke product van het verschil toe te passen met de som gelijk aan het verschil in kwadraten, hebben we:

z '= x'^twee - Y '^twee

wat duidelijk overeenkomt met de aanvankelijk gegeven definitie van hyperbolische paraboloïde.

Het onderscheppen van de vlakken parallel aan de XY-as met de hyperbolische paraboloïde z = x en het bepalen van gelijkzijdige hyperbolen die als asymptoten de vlakken x = 0 en y = 0 hebben.

- Voorbeeld 2

Bepaal de parameters naar Y b van de hyperbolische paraboloïde die door de punten A (0, 0, 0) gaat; B (1, 1, 5/9); C (-2, 1, 32/9) en D (2, -1, 32/9).

Oplossing

Volgens zijn eigenschappen bepalen vier punten in de driedimensionale ruimte een enkele hyperbolische paraboloïde. De algemene vergelijking is:

z = (x / a)^twee - (en B)^twee

We vervangen de gegeven waarden:

Voor punt A geldt 0 = (0 / a)^twee - (0 / b)^twee, vergelijking waaraan wordt voldaan, ongeacht de waarden van de parameters a en b.

Als we punt B vervangen, krijgen we:

5/9 = 1 / a^twee - 1 B.^twee

Terwijl voor punt C blijft:

32/9 = 4 / a^twee - 1 B.^twee

Ten slotte krijgen we voor punt D:

32/9 = 4 / a^twee - 1 B.^twee

Dat is identiek aan de vorige vergelijking. Uiteindelijk moet het stelsel vergelijkingen worden opgelost:

5/9 = 1 / a^twee - 1 B.^twee

32/9 = 4 / a^twee - 1 B.^twee

Het aftrekken van de tweede vergelijking van de eerste geeft:

27/9 = 3 / a^twee wat inhoudt dat a^twee = 1.

Evenzo wordt de tweede vergelijking afgetrokken van het viervoud van de eerste en verkrijgt men:

(32-20) / 9 = 4 / a^twee - 4 / a^twee -1 B.^twee + 4 / b^twee

Dat is vereenvoudigd als:

12/9 = 3 / b^twee ⇒ b^twee = 9/4.

Kortom, de hyperbolische paraboloïde die door de gegeven punten A, B, C en D gaat, heeft een cartesische vergelijking die wordt gegeven door:

z = x^twee - (4/9) en^twee

- Voorbeeld 3

Volgens de eigenschappen van de hyperbolische paraboloïde passeren twee lijnen elk punt dat er volledig in zit. Zoek voor het geval z = x ^ 2 - y ^ 2 de vergelijking van de twee lijnen die door het punt P (0, 1, -1) gaan, duidelijk behorende tot de hyperbolische paraboloïde, zodat alle punten van deze lijnen ook horen naar hetzelfde.

Oplossing

Met behulp van het opmerkelijke product van het verschil in kwadraten kan de vergelijking voor de hyperbolische paraboloïde als volgt worden geschreven:

(x + y) (x - y) = c z (1 / c)

Waar c een constante is die niet nul is.

De vergelijking x + y = c z, en de vergelijking x - y = 1 / c komen overeen met twee vlakken met normaalvectoren n​<1,1,-c> Y m​<1,-1,0>. Het vectorproduct m x n ​<-c, -c, -2> geeft ons de richting van de snijlijn van de twee vlakken. Dan heeft een van de lijnen die door het punt P loopt en tot de hyperbolische paraboloïde behoort een parametervergelijking:

​ <0, 1, -1> + t <-c, -c, -2>

Om c te bepalen, vervangen we het punt P in de vergelijking x + y = c z en krijgen we:

c = -1

Op een vergelijkbare manier, maar gezien de vergelijkingen (x - y = k z) en (x + y = 1 / k), hebben we de parametervergelijking van de regel:

​ <0, 1, -1> + s met k = 1.

Samengevat, de twee regels:

​ <0, 1, -1> + t <1, 1, -2> Y  ​ <0, 1, -1> + s <1, -1, 2>

Ze zijn volledig vervat in de hyperbolische paraboloïde z = x^twee - Y^twee passeren door het punt (0, 1, -1).

Stel ter controle t = 1, wat ons het punt (1,2, -3) op de eerste regel geeft. Je moet kijken of het ook op de paraboloïde z = x staat^twee - Y^twee​

-3 = 1^twee - twee^twee = 1 - 4 = -3

Wat bevestigt dat het inderdaad tot het oppervlak van de hyperbolische paraboloïde behoort.

De hyperbolische paraboloïde in de architectuur

De hyperbolische paraboloïde is in de architectuur gebruikt door de grote avant-gardistische architecten, waaronder de namen van de Spaanse architect Antoni Gaudí (1852-1926) en vooral de eveneens Spaanse Félix Candela (1910-1997)..

Hieronder staan ​​enkele werken gebaseerd op de hyperbolische paraboloïde:

-Kapel van de stad Cuernavaca (Mexico) werk van de architect Félix Candela.

-Oceanografisch van Valencia (Spanje), eveneens door Félix Candela.

Referenties

1. Encyclopedie van de wiskunde. Geleid oppervlak. Hersteld van: encyclopediaofmath.org
2. Llera Rubén. Hyperbolische paraboloïde. Hersteld van: rubenllera.wordpress.com
3. Weisstein, Eric W. "Hyperbolische paraboloïde." Van MathWorld-A Wolfram Web Resource. Hersteld van: mathworld.wolfram.com
4. Wikipedia. Paraboloïde. Hersteld van: en.wikipedia.com
5. Wikipedia. Paraboloïde. Hersteld van: es.wikipedia.com
6. Wikipedia. Geleid oppervlak. Hersteld van: en.wikipedia.com