
Hydrostatische drukformule, berekening, voorbeelden, oefeningen

De hydrostatische druk is degene die een vloeistof in statisch evenwicht uitoefent op elk punt in zijn inwendige, of het nu een oppervlak is dat erin is ondergedompeld, de wanden van de container of een deel van de vloeistof die deel uitmaakt van de totale massa.
De manier waarop vloeistoffen druk uitoefenen, verschilt van vaste stoffen. Deze oefenen een neerwaartse druk uit, maar een vloeistof of gas doet dat in alle richtingen.

Als het om een vloeistof gaat, neemt de druk toe met de diepte, zoals uit ervaring bekend is bij onderdompeling in water waarbij de drukverhoging in de oren voelbaar is. Deze druk komt van het gewicht van de vloeistof en de onophoudelijke beweging van de deeltjes waaruit het bestaat, die continu het oppervlak van het lichaam raken dat in de vloeistof is ondergedompeld..
Als we een onsamendrukbare vloeistof aannemen - wat waar is in de overgrote meerderheid van de toepassingen - blijft de dichtheid constant en in dit geval hangt de druk lineair af van de diepte..
Artikel index
- 1 Formule
- 2 Voorbeelden van hydrostatische druk
- 2.1 Constructies waar hydrostatische druk relevant is
- 3 oefeningen
- 3.1 - Oefening 1
- 3.2 - Oefening 2
- 4 referenties
Formule
Hydrostatische druk wordt berekend met behulp van de volgende uitdrukking:
P = PGeldautomaat + ρ · g · h
Waar:
-P de druk die op een bepaald punt wordt uitgeoefend
-P.Geldautomaat is de druk van de atmosfeer op het vrije oppervlak
-ρ is de dichtheid van de vloeistof
-g is de versnelling van de zwaartekracht
-h is de diepte waarop u de hydrostatische druk wilt berekenen
De formule omvat de effecten van de atmosfeer, maar veel manometers of manometers plaatsen 0 in de atmosferische druk, daarom meten ze de differentiële druk of relatieve druk, ook wel manometer druk
P.m = ρ · g · h
Wat betreft gassen, ze comprimeren of expanderen heel gemakkelijk. Daarom is de dichtheid, de verhouding tussen massa en volume, meestal een functie van andere parameters, zoals hoogte en temperatuur, in het geval van atmosferische gassen..
De druk die door gassen wordt uitgeoefend, wordt vaak genoemd aerostatische druk, de term hydrostatische druk wordt gereserveerd voor vloeistoffen.
Voorbeelden van hydrostatische druk
De hydrostatische druk is alleen afhankelijk van de diepte, dus de vorm of het oppervlak van de bodem van de container is niet relevant.
Aangezien druk P wordt gedefinieerd als de loodrechte krachtcomponent F per oppervlakte-eenheid A:
P = F / A
Dan kan de kracht die wordt uitgeoefend door de vloeistof op de bodem van een container anders zijn, maar aangezien deze wordt verdeeld over verschillende extensies, is de druk, de kracht / oppervlakteverhouding, hetzelfde voor punten op dezelfde diepte..
Beschouw de containers in de figuur. De druk is hetzelfde voor alle rode stippen die zich op hetzelfde niveau bevinden, hoewel er boven dat niveau in de centrale container meer vloeistof zit - breder - dan de cilindrische en dunne buis uiterst links..
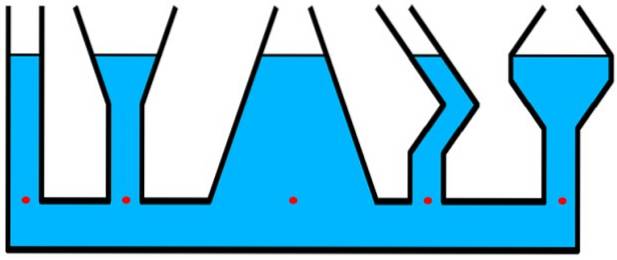
Constructies waar hydrostatische druk relevant is
-De wanden van een dam: hoewel de kracht hetzelfde is voor alle punten van de platte bodem, groeit deze op de verticale wand naarmate de diepte toeneemt, daarom zijn de keerwanden aan de basis breder dan aan de bovenkant.
-Op de muren en bodem van een zwembad.
-In sterren zoals onze zon, waar hydrostatische druk de zwaartekracht in evenwicht houdt en de ster in beweging houdt. Wanneer dit evenwicht wordt verbroken, stort de ster in en ondergaat hij extreme veranderingen in zijn structuur..
-Vloeistofopslagtanks, ontworpen om hydrostatische druk te weerstaan. Niet alleen de muren, maar ook de poorten die het vullen en afzuigen vergemakkelijken. Voor het ontwerp wordt er rekening mee gehouden of de vloeistof corrosief is en ook de druk en de kracht die het uitoefent in overeenstemming met de dichtheid.
-Banden en ballonnen, die zodanig worden opgeblazen dat ze de druk van de vloeistof (gas of vloeistof) weerstaan zonder te scheuren.
-Elk ondergedompeld lichaam dat een verticale opwaartse stuwkracht ervaart, of "verlichting" van zijn gewicht, dankzij de hydrostatische druk die door de vloeistof wordt uitgeoefend. Dit staat bekend als de Het principe van Archimedes.
Opleiding
Het principe van Archimedes stelt dat wanneer een lichaam geheel of gedeeltelijk onder water komt te staan, het een opwaartse verticale kracht zal ervaren, ook wel stuwkracht genoemd. De grootte van de stuwkracht is numeriek gelijk aan het gewicht van het volume water dat door het object wordt verplaatst..

Laat ρvloeistof de dichtheid van de vloeistof, Vs het ondergedompelde volume, g de versnelling van de zwaartekracht en B de grootte van de stuwkracht, die we kunnen berekenen met behulp van de volgende uitdrukking:
B = ρvloeistof .V.s .g
- Oefening 1
Een rechthoekig blok met de afmetingen 2,0 cm x 2,0 cm x 6,0 cm drijft in zoet water met de langste as verticaal. De lengte van het blok dat boven het water uitsteekt is 2,0 cm. Bereken de dichtheid van het blok.
Oplossing
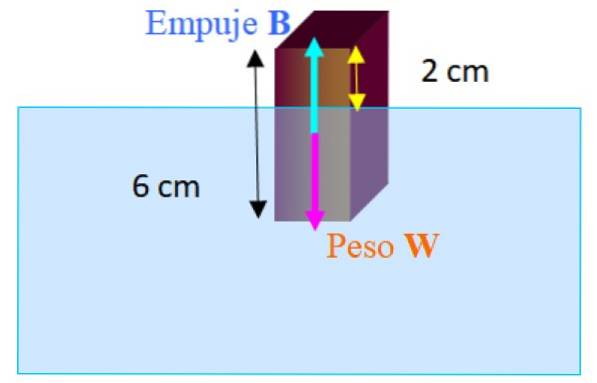
De krachten die op het blok werken, zijn het gewicht W. naar beneden en stuwkracht B. omhoog. Terwijl het blok in evenwicht zweeft, hebben we:
∑ F.Y = B - W = 0
B = W
De grootte van het gewicht W is het product van de massa m van het blok en de versnelling van de zwaartekracht. We zullen de definitie van de dichtheid ρ gebruikenof als het quotiënt tussen de massa m en het volume V. van het blok:
ρof = m / V → m = ρof . V.
De stuwkracht van zijn kant is:
B = ρvloeistof .V.s .g
De grootte van de stuwkracht en de grootte van het gewicht gelijkstellen:
ρvloeistof .V.s .g = ρof . V.g
De zwaartekracht wordt opgeheven door aan beide kanten een factor te zijn en de dichtheid van het blok kan worden opgelost als:
ρof = ρvloeistof . (V.s / V)
De dichtheid van water in International System-eenheden is 1000 kg / m3. De volumes zijn in totaal V en ondergedompeld Vs, worden berekend met V = breedte x hoogte x diepte:
V = 2,0 cm x 2,0 cm x 6,0 cm = 24,0 cm3
V.s = 2,0 cm x 2,0 cm x 4,0 cm = 16,0 cm3
Waarden vervangen:
ρof = ρvloeistof . (V.s / V) = 1000 kg / m3 . (16/24) = 667 kg / m3
- Oefening 2
Bereken het percentage van het ondergedompelde volume van een stuk ijs dat drijft in zeewater van 0 ºC.
Oplossing
IJs drijft op water, omdat de dichtheid lager is: 916,8 kg / m3, wat betekent dat het uitzet bij afkoeling, in tegenstelling tot de meeste stoffen, die bij verhitting in volume toenemen.

Het is een zeer gelukkige omstandigheid voor het leven, aangezien de watermassa's alleen aan het oppervlak bevriezen en in de diepte vloeibaar blijven.
De dichtheid van zeewater is iets hoger dan die van zoet water: 1027 Kg / m3. We zullen de volumefractie V berekenens / V:
V.s / V = ρof / ρvloeistof = 916,8 kg / m3 / 1027 kg / m3 = 0,8927
Dit betekent dat ongeveer 89% van het ijs onder water blijft staan. Slechts 11% is zichtbaar drijvend op zee.
Referenties
- Giambattista, A. 2010. Physics. 2e. Ed McGraw Hill.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Cimbala, C. 2006. Vloeistofmechanica, grondbeginselen en toepassingen. Mc. Graw Hill.
- Hibbeler, R. 2015. Vloeistofmechanica. 1e. Ed Pearson.
- Mott, R. 2006. Vloeistofmechanica. 4e. Editie. Pearson Education.
- Streeter, V. 1999. Fluid Mechanics. Mcgraw heuvel.


Niemand heeft nog op dit artikel gereageerd.