
Gage drukverklaring, formules, vergelijkingen, voorbeelden
De manometer druk P.m is dat wat wordt gemeten in relatie tot een referentiedruk, die in de meeste gevallen wordt gekozen als de atmosferische druk PGeldautomaat op zeeniveau. Het is dan een relatieve druk, een andere term waarmee het ook bekend is.
De andere manier waarop de druk gewoonlijk wordt gemeten, is door deze te vergelijken met het absolute vacuüm, waarvan de druk altijd nul is. In zo'n geval spreken we van de absolute druk, die we zullen aanduiden als Pnaar.
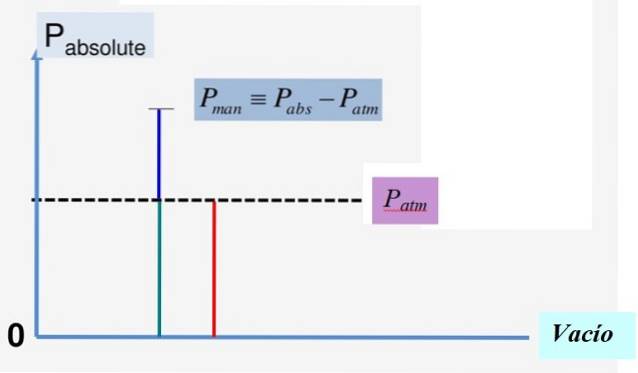
De wiskundige relatie tussen deze drie grootheden is:
P.naar = P.Geldautomaat + P.m
Daarom:
P.m = P.naar - P.Geldautomaat
Figuur 1 illustreert handig deze relatie. Omdat de vacuümdruk 0 is, is de absolute druk altijd positief en hetzelfde gebeurt met de atmosferische druk PGeldautomaat.
Meterdruk wordt vaak gebruikt om drukken boven de atmosferische druk aan te duiden, zoals die in banden of die op de bodem van de zee of een zwembad, die wordt uitgeoefend door het gewicht van de waterkolom. In deze gevallen is Pm > 0, aangezien Pnaar > BlzGeldautomaat.
Er zijn echter absolute drukken onder PGeldautomaat. In deze gevallen is Pm < 0 y recibe el nombre de Druk van leeg en niet te verwarren met druk van vacuüm al beschreven, namelijk de afwezigheid van deeltjes die druk kunnen uitoefenen.
Artikel index
- 1 Formules en vergelijkingen
- 1.1 Variatie van druk met diepte
- 2 voorbeelden
- 2.1 Het principe van Pascal
- 2.2 Stevin's hydrostatische paradox
- 3 oefeningen
- 3.1 Oefening 1
- 3.2 Oefening 2
- 4 referenties
Formules en vergelijkingen
De druk in een vloeistof -vloeistof of gas- is een van de belangrijkste variabelen in zijn onderzoek. In een stationair fluïdum is de druk ongeacht de oriëntatie op alle punten op dezelfde diepte gelijk, terwijl de beweging van fluïda in de leidingen wordt veroorzaakt door drukveranderingen..
De gemiddelde druk wordt gedefinieerd als het quotiënt tussen de kracht loodrecht op een oppervlak F. en het gebied van genoemd oppervlak A, dat wiskundig als volgt wordt uitgedrukt:
P = F /NAAR
Druk is een scalaire grootheid, waarvan de afmetingen kracht per oppervlakte-eenheid zijn. De meeteenheden in het International System of Units (SI) zijn newton / mtwee, genaamd Pascal en afgekort als Pa, ter ere van Blaise Pascal (1623-1662).
Veelvouden als kilo (103) Y mega (106) worden vaak gebruikt, aangezien de atmosferische druk meestal in het bereik van 90.000 - 102.000 Pa ligt, wat gelijk is aan: 90 - 102 kPa. Drukken in de orde van grootte van megapascals zijn niet ongebruikelijk, dus het is belangrijk om vertrouwd te raken met de voorvoegsels.
In Angelsaksische eenheden wordt de druk gemeten in ponden / voettwee, het wordt echter meestal gedaan in ponden / inchtwee of psi (pond-kracht per vierkante inch.
Variatie van druk met diepte
Hoe meer we ons onderdompelen in het water in een zwembad of in de zee, hoe meer druk we ervaren. Integendeel, naarmate de hoogte toeneemt, neemt de atmosferische druk af.
De gemiddelde atmosferische druk op zeeniveau wordt vastgesteld op 101.300 Pa of 101,3 kPa, terwijl deze in de Mariana Trench in de westelijke Stille Oceaan - de diepste bekende diepte - ongeveer 1000 keer groter is en op de top van Everest slechts 34 kPa..
Het is duidelijk dat druk en diepte (of hoogte) gerelateerd zijn. Om dit te achterhalen in het geval van een vloeistof in rust (statisch evenwicht), wordt een schijfvormig deel van de vloeistof beschouwd, opgesloten in een container, (zie figuur 2). De schijf heeft een dwarsdoorsnede NAAR, gewicht dW en hoogte dy.
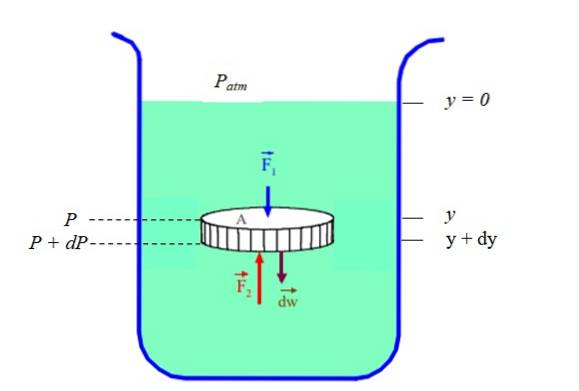
We zullen bellen P. naar de druk die op diepte bestaat "Y"Y P + dP op de druk die op diepte bestaat (y + dyOmdat de dichtheid ρ van de vloeistof de verhouding is van zijn massa dm en zijn volume dV, je moet:
ρ = dm / dV ⇒ dm = ρ.dV
Daarom het gewicht dW van het element is:
dW = g. dm = ρ.g.dV
En nu is de tweede wet van Newton van toepassing:
Σ F.Y F.twee - F.1 - dW = 0
(P + dP) .A - P.A - ρ.g.dV = 0
(P + dP) .A - P.A - ρ.g. A. dy = 0
dP = ρ.g.dy
Oplossing van de differentiaalvergelijking
Beide kanten integreren en gezien de dichtheid ρ, evenals zwaartekracht g constant zijn, wordt de gezochte uitdrukking gevonden:
P.twee - P.1 = ΔP = ρ.g. (entwee - Y1
ΔP = ρ.g. ΔY
Als u in de vorige uitdrukking kiest P.1 als atmosferische druk en Y1 dan als het oppervlak van de vloeistof Ytwee het bevindt zich op een diepte h Y AP = Ptwee - P.Geldautomaat is de overdruk als functie van de diepte:
P.m = ρ.g.h
Als u de absolute drukwaarde nodig heeft, voegt u de atmosferische druk toe aan het vorige resultaat.
Voorbeelden
Om de manometerdruk te meten, wordt een apparaat genoemd druk meter, die over het algemeen drukverschillen bieden. Aan het einde wordt het werkingsprincipe van een U-buismanometer beschreven, maar laten we nu eens kijken naar enkele belangrijke voorbeelden en consequenties van de eerder afgeleide vergelijking.
Pascal's principe
De vergelijking ΔP = ρ.g. (entwee - Y1 kan worden geschreven als P = Po + ρ.g.h, waar P. is de druk op diepte h, terwijl P.of is meestal de druk aan het oppervlak van de vloeistof P.Geldautomaat.
Het is duidelijk dat het elke keer toeneemt Po, stijgt P. in dezelfde hoeveelheid, zolang het maar een vloeistof is waarvan de dichtheid constant is. Het is precies wat er werd verondersteld bij het overwegen ρ constant en plaats deze buiten de integraal die in de vorige sectie is opgelost.
Het principe van Pascal stelt dat elke toename van de druk van een ingesloten vloeistof in evenwicht wordt overgedragen zonder enige variatie op alle punten van die vloeistof. Door deze eigenschap is het mogelijk om de kracht te vermenigvuldigen F.1 aangebracht op de kleine zuiger aan de linkerkant, en verkrijg F.twee aan de rechterkant.
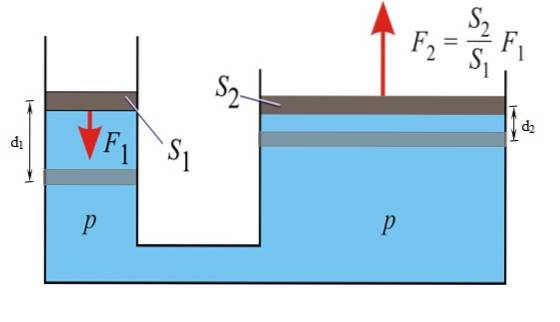
Autoremmen werken volgens dit principe: er wordt een relatief kleine kracht op het pedaal uitgeoefend, die dankzij de vloeistof die in het systeem wordt gebruikt een grotere kracht op de remcilinder bij elk wiel krijgt..
Stevin's hydrostatische paradox
De hydrostatische paradox stelt dat de kracht als gevolg van de druk van een vloeistof op de bodem van een container gelijk, groter of kleiner kan zijn dan het gewicht van de vloeistof zelf. Maar als je de container bovenop de weegschaal zet, registreert hij normaal gesproken het gewicht van de vloeistof (plus dat van de container natuurlijk). Hoe deze paradox te verklaren?
We gaan uit van het feit dat de druk op de bodem van de container uitsluitend afhangt van de diepte en onafhankelijk is van de vorm, zoals werd afgeleid in de vorige paragraaf.
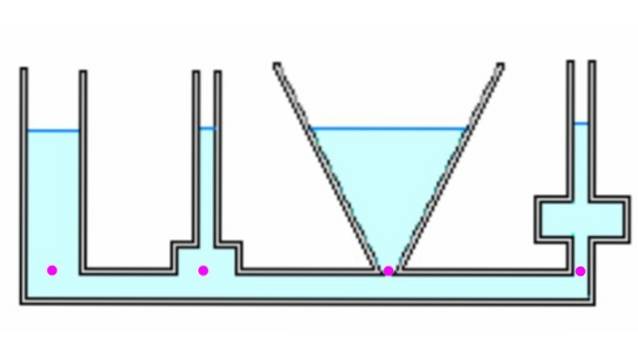
Laten we eens kijken naar een paar verschillende containers. Als ze worden gecommuniceerd, bereiken ze allemaal dezelfde hoogte wanneer ze zich vullen met vloeistof h. De hoogtepunten staan op dezelfde druk, omdat ze zich op dezelfde diepte bevinden. De kracht als gevolg van druk op elk punt kan echter verschillen van het gewicht (zie voorbeeld 1 hieronder).
Opleiding
Oefening 1
Vergelijk de kracht die wordt uitgeoefend door de druk op de bodem van elk van de containers met het gewicht van de vloeistof en leg uit waarom de eventuele verschillen.
Container 1
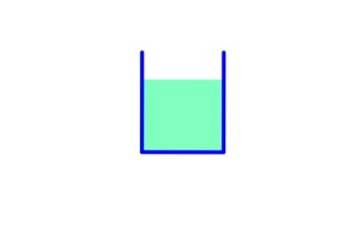
In deze container is het oppervlak van de basis A, dus:
Vloeistofgewicht: mg = ρ.V.g = ρ . Ah. g
Druk op de bodem: ρ. g. h
Kracht door druk: F = P.A = ρ. g. h. NAAR
Gewicht en kracht door druk zijn gelijk.
Container 2
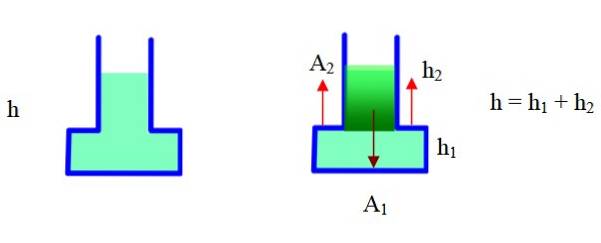
De container heeft een smal deel en een breed deel. In het diagram aan de rechterkant is het opgedeeld in twee delen en wordt de geometrie gebruikt om het totale volume te vinden. Gebied Atwee het is extern naar de container, htwee is de hoogte van het smalle gedeelte, h1 is de hoogte van het brede deel (basis).
Het volledige volume is het volume van de basis + het volume van het smalle gedeelte. Met deze gegevens hebben we:
Vloeistofgewicht: m. g = ρ . g. V = ρ . g. [NAAR1 .h1+ (NAAR1 -NAARtwee) .htwee
= ρ . g (EEN1.hatweehtwee) = ρ . g. NAAR1.h - ρ . g. NAAR.. htwee (Er is gebruik gemaakt van h = h1 +htwee
Druk op de bodem: P = ρ. g. h
Kracht op de bodem door druk: F = P. A1 = ρ. g. h. NAAR1
Door het gewicht van de vloeistof te vergelijken met de kracht als gevolg van druk, blijkt dat dit groter is dan het gewicht.
Wat er gebeurt, is dat de vloeistof ook kracht uitoefent van de kant van de stap in de container (zie de pijlen in rood in de figuur) die in bovenstaande berekening zijn meegenomen. Deze opwaartse kracht werkt de neerwaartse kracht tegen en het door de weegschaal geregistreerde gewicht is hiervan het resultaat. Volgens dit is de grootte van het gewicht:
W = Kracht op de bodem - Kracht op het getrapte deel = ρ . g. NAAR1.h - ρ . g. NAAR.. htwee
Oefening 2
In de afbeelding wordt een manometer met open buis getoond. Het bestaat uit een U-vormige buis, waarvan het ene uiteinde op atmosferische druk staat en het andere is verbonden met S, het systeem waarvan de druk moet worden gemeten..
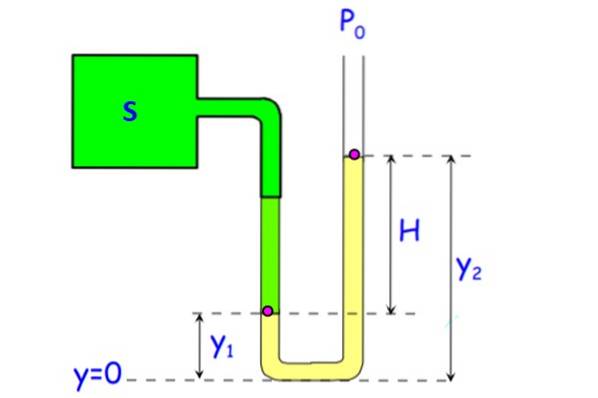
De vloeistof in de buis (in de afbeelding geel weergegeven) kan water zijn, hoewel bij voorkeur kwik wordt gebruikt om de grootte van het apparaat te verkleinen. (Een verschil van 1 atmosfeer of 101,3 kPa vereist een waterkolom van 10,3 meter, niets draagbaar).
Het vraagt om de meterdruk te vinden P.m in systeem S, als functie van de hoogte H van de vloeistofkolom.
Oplossing
De druk aan de onderkant voor beide takken van de buis is hetzelfde, aangezien ze zich op dezelfde diepte bevinden. Laat PNAAR de druk op punt A, gelegen op y1 En PB die van punt B dat is ter hoogte van entwee. Aangezien punt B zich op het grensvlak van vloeistof en lucht bevindt, is de druk daar Pof. In deze tak van de manometer is de druk onderaan:
Po + ρ.g.ytwee
Van zijn kant is de druk onderaan voor de tak aan de linkerkant:
P + ρ.g.y1
Waarbij P de absolute druk van het systeem is en ρ de dichtheid van de vloeistof. Beide drukken gelijk maken:
Po + ρ.g.ytwee P + ρ.g.y1
Opruimen P.
P = Po + ρ.g.ytwee - ρ.g.y1 = Po + ρ.g (entwee - Y1) = Po + ρ.g. H.
Daarom is de manometerdruk P.m is gegeven door P - Pof = ρ.g. H. en om zijn waarde te hebben, meet u gewoon de hoogte tot waar de manometrische vloeistof stijgt en vermenigvuldigt u deze met de waarde van g en de dichtheid van de vloeistof.
Referenties
- Cimbala, C. 2006. Vloeistofmechanica, grondbeginselen en toepassingen. Mc. Graw Hill. 66-74.
- Figueroa, D. 2005. Serie: Physics for Sciences and Engineering. Deel 4. Vloeistoffen en thermodynamica. Bewerkt door Douglas Figueroa (USB). 3-25.
- Mott, R. 2006. Vloeistofmechanica. 4e. Editie. Pearson Education. 53-70.
- Shaugnessy, E. 2005. Inleiding tot vloeistofmechanica, Oxford University Press. 51 - 60.
- Stylianos, V. 2016. Een eenvoudige uitleg van de klassieke hydrostatische paradox. Hersteld van: haimgaifman.files.wordpress.com



Niemand heeft nog op dit artikel gereageerd.