
Quadrangular Prism-formule en volume, kenmerken
EEN Vierkant prisma Het is er een waarvan het oppervlak wordt gevormd door twee gelijke bases die vierhoeken zijn en door vier zijvlakken die parallellogrammen zijn. Ze kunnen worden geclassificeerd op basis van hun hellingshoek en de vorm van hun basis.
Een prisma is een onregelmatig geometrisch lichaam met platte vlakken en deze omsluiten een eindig volume, dat is gebaseerd op twee polygonen en laterale vlakken die parallellogrammen zijn. Afhankelijk van het aantal zijden van de polygonen van de bases, kunnen de prisma's zijn: driehoekig, vierhoekig, vijfhoekig, onder andere.

Kenmerken hoeveel gezichten, hoekpunten en randen het heeft?
Een prisma met een vierhoekige basis is een veelvlakkige figuur met twee gelijke en evenwijdige bases en vier rechthoeken die de zijvlakken zijn die de corresponderende zijden van de twee bases met elkaar verbinden..
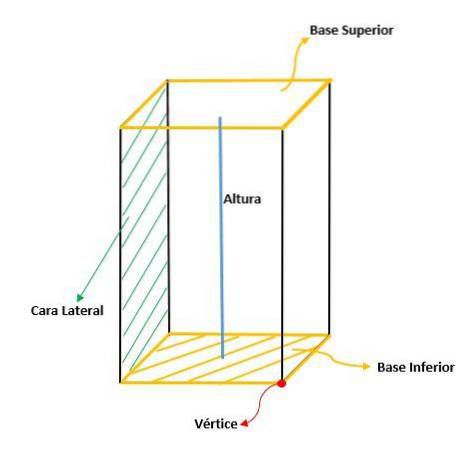
Het vierhoekige prisma kan worden onderscheiden van de andere soorten prisma's, omdat het de volgende elementen heeft:
Basissen (B)
Het zijn twee polygonen gevormd door vier zijden (vierhoek), die gelijk en parallel zijn.
Gezichten (C)
In totaal heeft dit type prisma zes vlakken:
- Vier zijvlakken gevormd door rechthoeken.
- Twee vlakken die de vierhoeken zijn die de basis vormen.
Hoekpunten (V)
Het zijn die punten waar drie vlakken van het prisma samenvallen, in dit geval zijn er in totaal 8 hoekpunten.
Randen: (A)
Het zijn segmenten waar twee vlakken van het prisma samenkomen en deze zijn:
- Basisranden: het is de verbindingslijn tussen een zijvlak en een basis, er zijn er in totaal 8.
- Zijranden: het is de laterale verbindingslijn tussen twee vlakken, er zijn er in totaal 4.
Het aantal randen van een veelvlak kan ook worden berekend met de stelling van Euler, als het aantal hoekpunten en vlakken bekend is; dus voor het vierhoekige prisma wordt het als volgt berekend:
Aantal randen = aantal vlakken + aantal hoekpunten - 2.
Aantal randen = 6 + 8 - 2.
Aantal randen = 12.
Hoogte (h)
De hoogte van het vierhoekige prisma wordt gemeten als de afstand tussen de twee bases.
Classificatie
Vierhoekige prisma's kunnen worden geclassificeerd op basis van hun hellingshoek, die recht of schuin kan zijn:
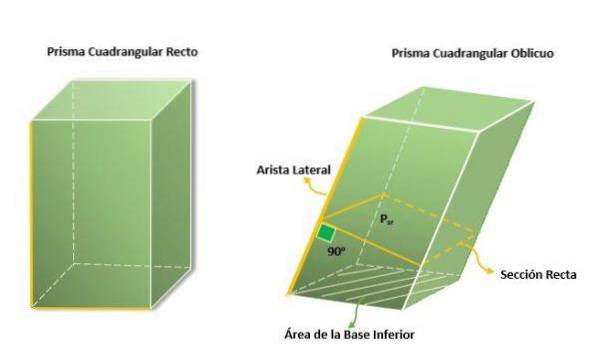
Rechte vierhoekige prisma's
Ze hebben twee gelijke en evenwijdige vlakken, die de basis vormen van het prisma, hun zijvlakken worden gevormd door vierkanten of rechthoeken, op deze manier zijn hun zijranden allemaal gelijk en is hun lengte gelijk aan de hoogte van het prisma..
De totale oppervlakte wordt bepaald door de oppervlakte en omtrek van de basis, door de hoogte van het prisma:
At = Akant + 2Abaseren.
Schuine vierhoekige prisma's
Dit type prisma wordt gekenmerkt doordat de zijvlakken schuine tweevlakshoeken vormen met de basis, dat wil zeggen dat de zijvlakken niet loodrecht op de basis staan, aangezien ze een hellingsgraad hebben die kleiner of groter kan zijn dan 90of.
De zijvlakken zijn in het algemeen parallellogrammen met een ruit- of ruitvorm en kunnen een of meer rechthoekige vlakken hebben. Een ander kenmerk van deze prisma's is dat hun hoogte verschilt van de afmetingen van hun zijranden..
Het gebied van een schuin vierhoekig prisma wordt bijna hetzelfde berekend als de vorige, waarbij het gebied van de bases wordt opgeteld bij het laterale gebied; het enige verschil is de manier waarop het zijoppervlak wordt berekend.
Het oppervlak van de lateralen wordt berekend met een laterale rand en de omtrek van het rechte gedeelte van het prisma, dat is precies waar een hoek van 90 wordt gevormdof met elk van de zijkanten.
NAARtotaal = 2 Oppervlaktebaseren + OmtrekDhr * Randkant
Het volume van alle soorten prisma's wordt berekend door het oppervlak van de basis te vermenigvuldigen met de hoogte:
V = Gebiedbaseren hoogte = Ab h.
Op dezelfde manier kunnen vierhoekige prisma's worden geclassificeerd volgens het type vierhoek dat de bases vormen (regelmatig en onregelmatig):
Regelmatig vierhoekig prisma
Het is er een met twee vierkanten als basis en de zijvlakken zijn gelijke rechthoeken. Zijn as is een ideale lijn die evenwijdig loopt aan zijn gezichten en eindigt in het midden van zijn twee bases..

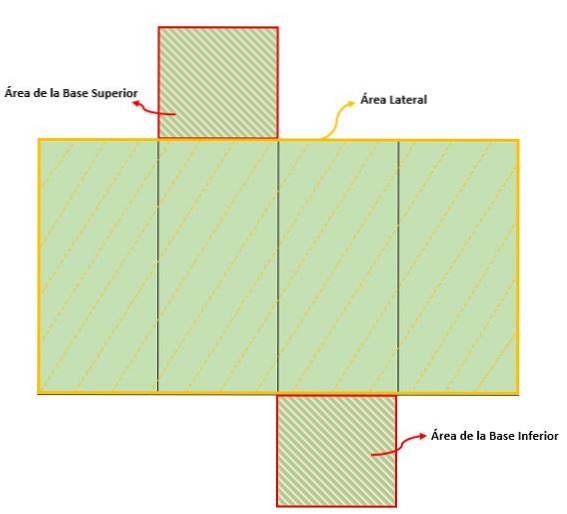
Om het totale oppervlak van een vierhoekig prisma te bepalen, moet het oppervlak van de basis en het laterale oppervlak worden berekend, zodat:
At = Akant + 2Abaseren.
Waar:
Het laterale gebied komt overeen met het gebied van een rechthoek; namelijk:
NAAR kant = Basis Hoogte = B h.
De oppervlakte van de basis komt overeen met de oppervlakte van een vierkant:
NAAR baseren = 2 (zijkant Zijde) = 2Ltwee
Om het volume te bepalen, vermenigvuldigt u het oppervlak van de basis met de hoogte:
V = EEN baseren Hoogte = Ltwee h
Onregelmatig vierhoekig prisma
Dit type prisma wordt gekenmerkt doordat de bases niet vierkant zijn; kan bases hebben die uit ongelijke zijden bestaan, en er worden vijf gevallen gepresenteerd waarin:
naar. De bases zijn rechthoekig
Het oppervlak wordt gevormd door twee rechthoekige bases en door vier zijvlakken die ook rechthoeken zijn, allemaal gelijk en parallel..
Om het totale oppervlak te bepalen, wordt elk gebied van de zes rechthoeken waaruit het bestaat, twee bases, twee kleine zijvlakken en de twee grote zijvlakken berekend:
Gebied = 2 (a b + ah + bh)

b. De bases zijn diamanten:
Het oppervlak wordt gevormd door twee ruitvormige bases en door vier rechthoeken die de zijvlakken zijn, om het totale oppervlak te berekenen, moet het worden bepaald:
- Basisoppervlak (ruit) = (hoofddiagonaal kleine diagonaal) ÷ 2.
- Lateraal gebied = omtrek van de basis hoogte = 4 (zijkanten van basis) * h
De totale oppervlakte is dus: AT = Akant + 2Abaseren.

c. De bases zijn ruitvormig
Het oppervlak wordt gevormd door twee ruitvormige bases en door vier rechthoeken die de zijvlakken zijn, het totale oppervlak wordt bepaald door:
- Basisoppervlak (ruitvormig) = basis relatieve hoogte = B * h.
- Lateraal gebied = omtrek van de basis hoogte = 2 (zijde a + zijde b) h
- Dus de totale oppervlakte is: AT = Akant + 2Abaseren.
d. De bases zijn trapeziums
Het oppervlak wordt gevormd door twee bases in de vorm van trapeziums en door vier rechthoeken die de zijvlakken zijn, het totale oppervlak wordt bepaald door:
- Basisoppervlak (trapezium) = h [(zijde a + zijde b) ÷ (2)].
- Lateraal gebied = omtrek van de basis hoogte = (a + b + c + d) * h
- Dus de totale oppervlakte is: AT = Akant + 2Abaseren.

en. De bases zijn trapeziums
Het oppervlak wordt gevormd door twee trapeziumvormige bases en door vier rechthoeken die de zijvlakken zijn, het totale oppervlak wordt bepaald door:
- Basisoppervlak (trapezium) = = (diagonaal1 * diagonaaltwee) ÷ 2.
- Lateraal gebied = omtrek van de basis hoogte = 2 (zijde a kant b * h.
- Dus de totale oppervlakte is: AT = Akant + 2Abaseren.
Samenvattend, om het gebied van een normaal vierhoekig prisma te bepalen, is het alleen nodig om het gebied van de vierhoek dat de basis is, zijn omtrek en de hoogte te berekenen die het prisma zal hebben, in het algemeen, zijn formule zou worden:
Oppervlakte Totaal = 2 Oppervlaktebaseren + Omtrekbasis * hoogte = A = 2Ab + P.b h.
Om het volume voor dit soort prisma's te berekenen, wordt dezelfde formule gebruikt, namelijk:
Volume = gebiedbaseren hoogte = Ab h.
Referenties
- Ángel Ruiz, H. B. (2006). Geometrieën. CR-technologie, .
- Daniel C. Alexander, G. M. (2014). Elementaire meetkunde voor studenten. Cengage leren.
- Maguiña, R. M. (2011). Geometrie achtergrond. Lima: UNMSM Pre-universitair centrum.
- Ortiz Francisco, O. F. (2017). Wiskunde 2.
- Pérez, A. Á. (1998). Álvarez Second Grade Encyclopedia.
- Pugh, A. (1976). Veelvlakken: een visuele benadering. Californië: Berkeley.
- Rodríguez, F. J. (2012). Beschrijvende geometrie Deel I. Tweevlakshoeksysteem. Donostiarra Sa.


Niemand heeft nog op dit artikel gereageerd.