De voorwaardelijke kans Het is de mogelijkheid dat een bepaalde gebeurtenis plaatsvindt, aangezien een andere zich voordoet als een aandoening. Deze aanvullende informatie kan (of niet) de perceptie wijzigen dat er iets zal gebeuren.
We kunnen ons bijvoorbeeld afvragen: "Hoe groot is de kans dat het vandaag gaat regenen, aangezien het al twee dagen niet heeft geregend?" De gebeurtenis waarvan we de kans willen weten, is dat het vandaag regent, en de aanvullende informatie die het antwoord zou bepalen, is dat "het al twee dagen niet heeft geregend".
Wees een probabilistische ruimte samengesteld uit Ω (steekproefruimte), ℬ (de willekeurige gebeurtenissen) en P (de waarschijnlijkheid van elke gebeurtenis), plus de gebeurtenissen A en B die bij ℬ horen.
De voorwaardelijke kans dat A optreedt, gegeven dat B is opgetreden, die wordt aangeduid als P (A│B), wordt als volgt gedefinieerd:
P (A│B) = P (A∩B) / P (B) = P (A en B) / P (B)
Waarbij: P (A) is de kans op optreden van A, P (B) is de kans op gebeurtenis B en verschilt van 0, en P (A∩B) is de kans op het snijpunt tussen A en B, dat wil zeggen `` de kans dat beide gebeurtenissen plaatsvinden (gezamenlijke waarschijnlijkheid).
Dit is een uitdrukking voor de stelling van Bayes toegepast op twee gebeurtenissen, in 1763 voorgesteld door de Engelse theoloog en wiskundige Thomas Bayes.
Artikel index
-Elke voorwaardelijke kans ligt tussen 0 en 1:
0 ≤ P (A│B) ≤ 1
-De kans dat gebeurtenis A plaatsvindt, gegeven dat gebeurtenis plaatsvindt, is uiteraard 1:
P (A│A) = P (A∩A) / P (A) = P (A) / P (A) = 1
-Als twee gebeurtenissen exclusief zijn, dat wil zeggen gebeurtenissen die niet tegelijkertijd kunnen plaatsvinden, dan is de voorwaardelijke kans dat een van hen plaatsvindt 0, aangezien het snijpunt nul is:
P (A│B) = P (A∩B) / P (B) = 0 / P (B) = 0
-Als B een deelverzameling is van A, dan is de voorwaardelijke kans ook 1:
P (B│A) = P (A∩B) / P (A) = 1
Belangrijk
P (A│B) is over het algemeen niet gelijk aan P (B│A), daarom moeten we oppassen dat we de gebeurtenissen niet uitwisselen bij het vinden van de voorwaardelijke waarschijnlijkheid.
Vaak wil je de gezamenlijke kans P (A∩B) vinden, in plaats van de voorwaardelijke kans. Dan hebben we via de volgende stelling:
P (A∩B) = P (A en B) = P (A│B). P (B)
De stelling kan worden uitgebreid voor drie gebeurtenissen A, B en C:
P (A∩B∩C) = P (A en B en C) = P (A) P (B│A) P (C│A∩B)
En ook voor diverse evenementen, zoals A1, NAARtwee, NAAR3 en meer, het kan als volgt worden uitgedrukt:
VADER1∩ EENtwee ∩ EEN3… ∩ An) = P (EEN1VADERtwee│A1VADER3│A1∩ EENtwee) ... VADERn││A1∩ EENtwee∩… An-1
Als het gaat om gebeurtenissen die in volgorde en in verschillende stadia plaatsvinden, is het handig om de gegevens in een diagram of tabel te ordenen. Dit maakt het eenvoudiger om de opties te visualiseren om de gevraagde kans te bereiken..
Voorbeelden hiervan zijn boomdiagram en de kruistabel. Van de ene kun je de andere bouwen.
Laten we eens kijken naar enkele situaties waarin de waarschijnlijkheid van de ene gebeurtenis wordt veranderd door het optreden van een andere:
In een snoepwinkel worden twee soorten taarten verkocht: aardbei en chocolade. Door de voorkeuren van 50 cliënten van beide geslachten te registreren, zijn de volgende waarden bepaald:
-27 vrouwen, waarvan 11 de voorkeur geven aan aardbeientaart en 16 chocoladetaart.
-23 mannen: 15 kiezen voor chocolade en 8 voor aardbei.
De kans dat een klant een chocoladetaart kiest, kan worden bepaald door de regel van Laplace toe te passen, volgens welke de waarschijnlijkheid van een gebeurtenis is:
P = aantal gunstige evenementen / totaal aantal evenementen
In dit geval geven van de 50 klanten in totaal 31 de voorkeur aan chocolade, dus de kans is P = 31/50 = 0,62. Dat wil zeggen, 62% van de klanten geeft de voorkeur aan chocoladetaart.
Maar zou het anders zijn als de cliënt een vrouw is? Dit is een geval van voorwaardelijke waarschijnlijkheid.
Met een kruistabel als deze worden de totalen eenvoudig weergegeven:
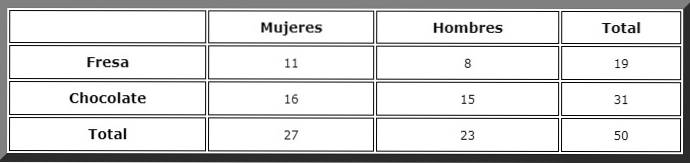
Vervolgens worden de gunstige gevallen in acht genomen en wordt de regel van Laplace toegepast, maar eerst definiëren we de gebeurtenissen:
-B is de "vrouwelijke klant" -gebeurtenis.
-A is de gebeurtenis "verkies chocoladetaart" als vrouw.
We gaan naar de kolom met het label "vrouwen" en daar zien we dat het totaal 27 is.
Dan wordt het gunstige geval gezocht in de "chocolade" rij. Er zijn 16 van deze gebeurtenissen, daarom is de gezochte kans direct:
P (A│B) = 16/27 = 0,5924
59,24% van de vrouwelijke klanten geeft de voorkeur aan chocoladetaart.
Deze waarde valt samen wanneer we het contrasteren met de aanvankelijk gegeven definitie van voorwaardelijke waarschijnlijkheid:
P (A│B) = P (A∩B) / P (B)
We zorgen ervoor dat we de regel van Laplace en de waarden van de tabel gebruiken:
P (B) = 27/50
P (A en B) = 16/50
Waar P (A en B) de kans is dat de klant chocolade verkiest en een vrouw is. Nu worden de waarden vervangen:
P (A│B) = P (A en B) / P (B) = (16/50) / (27/50) = 16/27 = 0,5924.
En het is bewezen dat het resultaat hetzelfde is.
In dit voorbeeld is de regel van vermenigvuldiging van toepassing. Stel dat er in een winkel broeken in drie maten te zien zijn: klein, middelgroot en groot..
In een kavel met in totaal 24 broeken, waarvan er 8 van elke maat zijn en allemaal gemengd, wat zou de kans zijn om er twee uit te halen en dat ze allebei klein waren?
Het is duidelijk dat de kans om bij de eerste poging een broekje uit te trekken 8/24 = 1/3 is. Nu is de tweede extractie geconditioneerd tot de eerste gebeurtenis, want bij het verwijderen van een broek zijn er niet meer 24, maar 23. En als een kleine broek wordt verwijderd, zijn er 7 in plaats van 8.
Gebeurtenis A trekt een kleine broek aan, nadat hij bij de eerste poging een andere heeft getrokken. En evenement B is degene met de kleine broek voor het eerst. Daarom:
P (B) = 1/3; P (A│B) = 7/24
Gebruik ten slotte de vermenigvuldigingsregel:
P (A∩B) = (7/24). (1/3) = 7/72 = 0,097
In een onderzoek naar punctualiteit op commerciële luchtvluchten zijn de volgende gegevens beschikbaar:
-P (B) = 0,83, is de kans dat een vliegtuig op tijd opstijgt.
-P (A) = 0,81, is de kans om op tijd te landen.
-P (B∩A) = 0,78 is de kans dat de vlucht op tijd aankomt en op tijd opstijgt.
Er wordt gevraagd om te berekenen:
a) Wat is de kans dat het vliegtuig op tijd zal landen, gezien het feit dat het op tijd vertrok?
b) Is de vorige kans hetzelfde als de kans dat hij op tijd vertrok als hij erin slaagde op tijd te landen??
c) En tot slot: wat is de kans dat het op tijd aankomt gezien dat niet kwam op tijd uit?
Om de vraag te beantwoorden, wordt de definitie van voorwaardelijke kans gebruikt:
P (A│B) = P (A∩B) / P (B) = P (A en B) / P (B) = 0,78 / 0,83 = 0,9398
In dit geval worden de gebeurtenissen in de definitie uitgewisseld:
P (B│A) = P (A∩B) / P (A) = P (A en B) / P (A) = 0,78 / 0,81 = 0,9630
Merk op dat deze kans enigszins verschilt van de vorige, zoals we eerder hebben aangegeven.
De kans om niet op tijd te vertrekken is 1 - P (B) = 1 - 0,83 = 0,17, we noemen het P (BC), omdat het de aanvullende gebeurtenis is om op tijd van start te gaan. De gezochte voorwaardelijke kans is:
P (A│BC) = P (A∩BC) / P (BC) = P (A en BC) / P (BC
Aan de andere kant:
P (A∩BC) = P (op tijd landen) - P (op tijd landen en op tijd opstijgen) = 0,81-0,78 = 0,03
In dit geval is de gezochte voorwaardelijke kans:
P (A│BC) = 0,03 / 0,17 = 0,1765
Niemand heeft nog op dit artikel gereageerd.