
Geometrische optica wat het bestudeert, wetten, toepassingen, oefeningen

De geometrische optica is de tak van de natuurkunde die zich richt op het bestuderen van de manier waarop licht zich verspreidt en weerkaatst wanneer het van het ene medium naar het andere gaat, zonder rekening te houden met de effecten van diffractie.
Op deze manier wordt licht geometrisch weergegeven door stralen, denkbeeldige lijnen loodrecht op de lichtgolffronten..
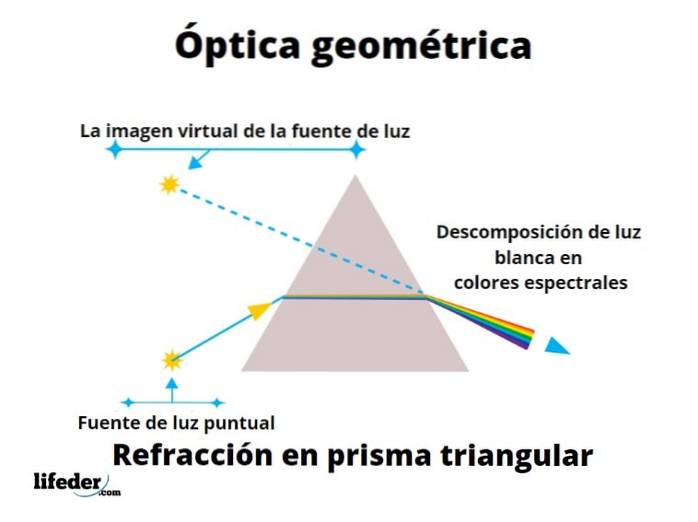
Lichtstralen komen uit lichtbronnen zoals de zon, een vlam of een gloeilamp en verspreiden zich in alle richtingen. Oppervlakken reflecteren deze lichtstralen gedeeltelijk en daarom kunnen we ze zien, dankzij het feit dat de ogen lichtgevoelige elementen bevatten.
Dankzij de straalbehandeling houdt geometrische optica niet zozeer rekening met de golfaspecten van licht, maar legt eerder uit hoe beelden worden gevormd in het oog, spiegels en projectoren, waar ze dat doen en hoe ze verschijnen..
De fundamentele principes van geometrische optica zijn de reflectie en breking van licht. Lichtstralen vallen onder bepaalde hoeken op de oppervlakken die ze ontmoeten, en dankzij dit helpt een eenvoudige geometrie om hun traject in elk medium bij te houden.
Dit verklaart alledaagse dingen zoals het kijken naar ons beeld in de badkamerspiegel, het zien van een theelepel die lijkt te buigen in een glas vol water, of het verbeteren van het gezichtsvermogen met een goede bril..
We hebben licht nodig om ons te verhouden tot de omgeving, daarom heeft zijn gedrag altijd waarnemers verbaasd, die zich afvroegen over de aard ervan..
Artikel index
- 1 Wat bestudeert geometrische optica? (Studieobject)
- 2 Basisconcepten in geometrische optica
- 2.1 Brekingsindex
- 2.2 Optisch pad
- 3 wetten van geometrische optica
- 3.1 Het principe van Fermat
- 3.2 Wet van reflectie
- 3.3 De wet van Snell
- 4 Toepassingen
- 4.1 Spiegels en lenzen
- 4.2 Optische instrumenten
- 4.3 Optische vezel
- 5 Oefening opgelost
- 5.1 Oplossing
- 6 referenties
Wat bestudeert geometrische optica? (Studieobject)
Geometrische optica bestudeert de voortplanting van licht in een vacuüm en in verschillende media, zonder uit te leggen waaruit de ware aard ervan bestaat. Hiervoor maakt het gebruik van het straalmodel en eenvoudige geometrie.
Een straal is het pad dat licht volgt in een bepaald transparant medium, wat een uitstekende benadering is zolang de golflengte klein is in vergelijking met de grootte van objecten..
Dit geldt in veel alledaagse gevallen, zoals in het begin genoemd..
Er zijn twee fundamentele premissen van geometrische optica:
-Het licht plant zich rechtlijnig voort.
-Terwijl het zich verspreidt via verschillende media, doet het dit volgens empirische wetten, dat wil zeggen verkregen door experimenten.
Basisconcepten in geometrische optica
Brekingsindex
De lichtsnelheid in een materiaalmedium is anders dan die van een vacuüm. Daar weten we dat het 300.000 km / s is, maar in de lucht is het net iets lager, en zelfs meer in water of glas..
De brekingsindex is een dimensieloze grootheid, die wordt gedefinieerd als het quotiënt tussen de snelheid waarmee licht reist in een vacuüm cof en snelheid c in genoemd medium:
n = cof / c
Optisch pad

Het is het product tussen de afstand die door licht wordt afgelegd om van het ene punt naar het andere te gaan, en de brekingsindex van het medium:
L = s. n
Waar L het optische pad is, is s de afstand tussen de twee punten en n vertegenwoordigt de brekingsindex, aangenomen dat het constant is.
Door middel van het optische pad worden lichtstralen die in verschillende media bewegen, vergeleken.
Invalshoek
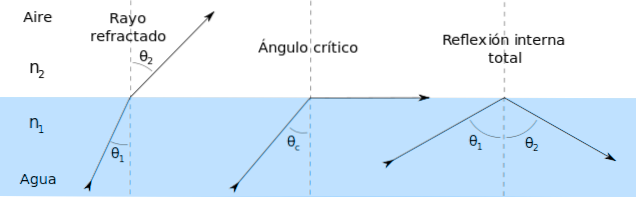
Het is de hoek die de lichtstraal vormt met de normale lijn naar een oppervlak dat twee media van elkaar scheidt.
Wetten van geometrische optica
Het principe van Fermat
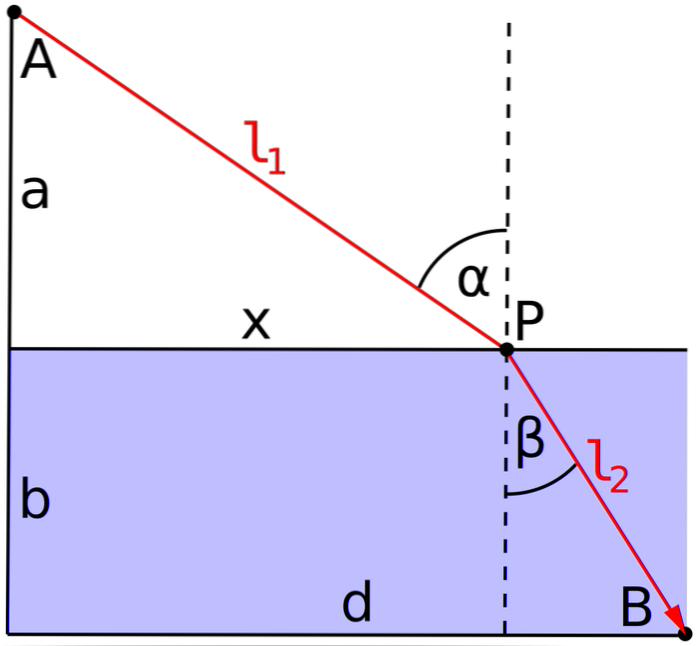
De Franse wiskundige Pierre de Fermat (1601-1665) merkte op dat:
Wanneer een lichtstraal tussen twee punten reist, volgt hij het pad waarin hij de minimale tijd nodig heeft.
En aangezien licht met constante snelheid beweegt, moet het pad rechtlijnig zijn.
Met andere woorden, het principe van Fermat stelt dat het pad van de lichtstraal zodanig is dat het optische pad tussen twee punten minimaal is..
Wet van reflectie
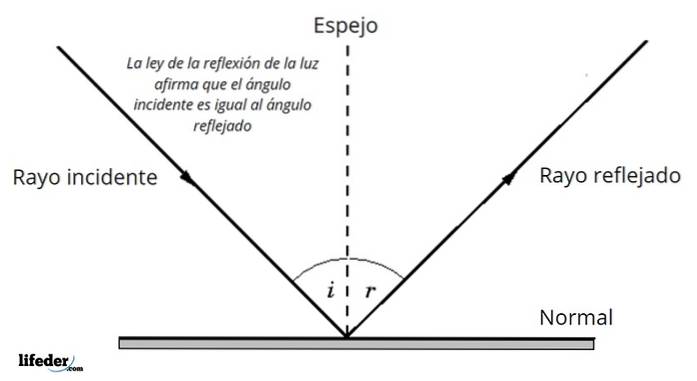
Bij het raken van het oppervlak dat twee verschillende media scheidt, wordt een deel van de invallende straal - of alles - teruggereflecteerd en doet dit met dezelfde gemeten hoek ten opzichte van de normaal op het oppervlak waarmee het raakte..

Met andere woorden, de invalshoek is gelijk aan de reflectiehoek:
θik = θik '
De wet van Snell
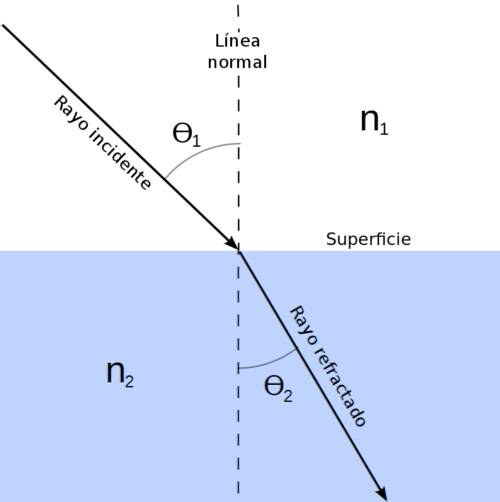
De Nederlandse wiskundige Willebrord Snell (1580-1626) observeerde zorgvuldig het gedrag van licht terwijl het van lucht naar water en glas gaat..
Hij zag dat wanneer een lichtstraal op het oppervlak valt dat twee media van elkaar scheidt en er een bepaalde hoek mee vormt, een deel van de straal wordt teruggekaatst naar het eerste medium en het andere deel door het tweede gaat..
Zo leidde hij de volgende relatie tussen beide media af:
n1 ⋅ sen θ1 = n2 ⋅ sen θtwee
Waar1 en Ntwee zijn de respectieve brekingsindices, terwijl θ1 Y θtwee zijn de invals- en brekingshoeken, gemeten ten opzichte van de normaal op het oppervlak, volgens de bovenstaande afbeelding.
Toepassingen
Spiegels en lenzen

Spiegels zijn hoogglans gepolijste oppervlakken die licht van objecten reflecteren, waardoor afbeeldingen kunnen worden gevormd. Platte spiegels, zoals die in de badkamer of die in een tas worden meegenomen, komen vaak voor.
Een lens bestaat uit een optisch apparaat met twee zeer nauwe refractieve oppervlakken. Wanneer een bundel parallelle stralen door een convergerende lens gaat, convergeren ze op een punt en vormen ze een beeld. Als het om een divergerende lens gaat, gebeurt het tegenovergestelde: de bundelstralen divergeren op een punt.
Lenzen worden vaak gebruikt om refractieafwijkingen in het oog te corrigeren, evenals in verschillende optische vergrotingsinstrumenten..
Optische instrumenten
Er zijn optische instrumenten waarmee afbeeldingen vergroot kunnen worden, bijvoorbeeld microscopen, vergrootglazen en telescopen. Er zijn er ook om boven ooghoogte te kijken, zoals periscopen.
Fotocamera's worden gebruikt om afbeeldingen vast te leggen en te bewaren, die een lenssysteem en een opname-element bevatten om het gevormde beeld op te slaan..
Glasvezel
Het is een lang, dun en transparant materiaal op basis van silica of plastic, dat wordt gebruikt voor datatransmissie. Het maakt gebruik van de eigenschap van totale reflectie: wanneer het licht het medium onder een bepaalde hoek bereikt, treedt er geen breking op, daarom kan de straal lange afstanden afleggen en in de gloeidraad stuiteren.
Oefening opgelost
Objecten op de bodem van een zwembad of vijver lijken dichterbij te zijn dan ze in werkelijkheid zijn, wat te wijten is aan refractie. Op welke schijnbare diepte ziet een waarnemer een munt die zich op de bodem van een 4 meter diep zwembad bevindt??
Stel dat de straal die uit de munt komt het oog van de waarnemer bereikt onder een hoek van 40 ° ten opzichte van de normaal..
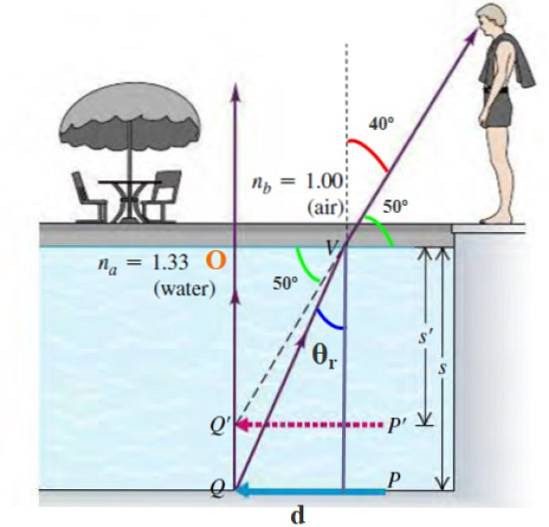
Feit: de brekingsindex van water is 1,33, die van lucht is 1.
Oplossing
De schijnbare diepte van de munt is s 'en de diepte van het zwembad is s = 4 m. De munt staat op punt Q en de waarnemer ziet hem op punt Q '. De diepte van dit punt is:
s '= s - Q'Q
Van de wet van Snell:
nb ⋅ zonde 40º = nnaar ⋅ sen θr
sen θr = (nb ⋅ zonde 40º) ÷ nnaar = sin 40º /1.33 = 0.4833
θr = arcsen (0,4833) = 28,9º
Als we deze hoek kennen, berekenen we de afstand d = OV vanaf de rechthoekige driehoek, waarvan de scherpe hoek is θr
tan 28,9º = OV / 4 m
OV = 4m × geelbruin 28,9º = 2,154 m
Aan de andere kant:
tan 50º = OQ '/ OV
Daarom:
OQ '= OV × tan 50º = 2,154 m × tan 50º = 2,57 m.
Referenties
- Bauer, W. 2011. Physics for Engineering and Sciences. Deel 2. Mc Graw Hill.
- Figueras, M. Geometrische optica: golfloze optica. Open Universiteit van Catalonië.
- Giancoli, D. 2006. Natuurkunde: principes met toepassingen. 6e. Ed Prentice Hall.
- Serway, R., Jewett, J. (2008). Physics for Science and Engineering. Deel 2. 7e. Ed. Cengage Learning.
- Tippens, P. 2011. Fysica: concepten en toepassingen. 7e editie. Mcgraw heuvel.



Niemand heeft nog op dit artikel gereageerd.