
Welke soorten integralen zijn er?

De soorten integralen die we in de calculus vinden, zijn de onbepaalde integralen en de bepaalde integralen. Hoewel bepaalde integralen veel meer toepassingen hebben dan onbepaalde integralen, is het noodzakelijk om eerst te leren hoe u onbepaalde integralen kunt oplossen..
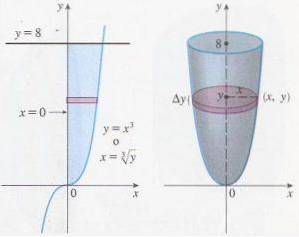
Een van de meest aantrekkelijke toepassingen van bepaalde integralen is de berekening van het volume van een omwentelingslichaam. Beide typen integralen hebben dezelfde lineariteitseigenschappen en ook de integratietechnieken zijn niet afhankelijk van het type integraal.
Maar ondanks dat ze erg op elkaar lijken, is er een belangrijk verschil; bij het eerste type integraal is het resultaat een functie (die niet specifiek is) terwijl bij het tweede type het resultaat een getal is.
Basistypen integralen
De wereld van integralen is erg breed, maar daarbinnen kunnen we twee basistypen van integralen onderscheiden, die een grote toepasbaarheid hebben in het dagelijks leven..
1- Onbepaalde integralen
Als F '(x) = f (x) voor alle x in het domein van f, zeggen we dat F (x) een primitief, een primitief of een integraal is van f (x).
Aan de andere kant, laten we opmerken dat (F (x) + C) '= F' (x) = f (x), wat impliceert dat de integraal van een functie niet uniek is, aangezien het geven van verschillende waarden aan de constante C zullen we verschillende primitieve waarden verkrijgen.
Om deze reden wordt F (x) + C de onbepaalde integraal van f (x) genoemd en wordt C de integratieconstante genoemd en we schrijven het als volgt
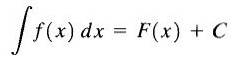
Zoals we kunnen zien, is de onbepaalde integraal van de functie f (x) een familie van functies.
Als je bijvoorbeeld de onbepaalde integraal van de functie f (x) = 3x² wilt berekenen, moet je eerst een primitief van f (x) vinden.
Het is gemakkelijk in te zien dat F (x) = x³ een primitief is, aangezien F '(x) = 3x². Daarom kan worden geconcludeerd dat
∫f (x) dx = ∫3x²dx = x³ + C.
2- Bepaalde integralen
Laat y = f (x) een reële, continue functie zijn op een gesloten interval [a, b] en laat F (x) een primitief zijn van f (x). De bepaalde integraal van f (x) tussen de limieten a en b wordt het getal F (b) -F (a) genoemd en wordt als volgt aangeduid
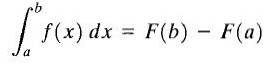
De bovenstaande formule is beter bekend als "The Fundamental Theorem of Calculus." Hier wordt "a" de ondergrens genoemd en "b" de bovengrens. Zoals je kunt zien, is de definitieve integraal van een functie een getal.
Als we in dit geval de bepaalde integraal van f (x) = 3x² in het interval [0,3] berekenen, krijgen we een getal.
Om dit aantal te bepalen kiezen we F (x) = x³ als primitief van f (x) = 3x². Vervolgens berekenen we F (3) -F (0) wat ons het resultaat 27-0 = 27 geeft. Concluderend, de definitieve integraal van f (x) op het interval [0,3] is 27.
Opgemerkt kan worden dat als G (x) = x³ + 3 wordt gekozen, G (x) een primitief is van f (x) verschillend van F (x), maar dit heeft geen invloed op het resultaat aangezien G (3) - G (0) = (27 + 3) - (3) = 27. Om deze reden verschijnt in de bepaalde integralen de integratieconstante niet.
Een van de meest bruikbare toepassingen van dit type integraal is dat het het mogelijk maakt om het oppervlak (volume) van een vlakke figuur (van een omwentelingslichaam) te berekenen, waarbij geschikte functies en integratiegrenzen (en een rotatieas) worden vastgesteld..
Binnen de gedefinieerde integralen kunnen we verschillende uitbreidingen ervan vinden, zoals lijnintegralen, oppervlakte-integralen, onjuiste integralen, meerdere integralen, onder andere, allemaal met zeer nuttige toepassingen in wetenschap en techniek..
Referenties
- Casteleiro, J. M. (2012). Is het gemakkelijk te integreren? Handleiding voor zelfstudie. Madrid: ESIC.
- Casteleiro, J. M., en Gómez-Álvarez, R. P. (2002). Integrale calculus (Geïllustreerde red.). Madrid: ESIC-redactie.
- Fleming, W., & Varberg, D. E. (1989). Precalculus wiskunde. Prentice Hall PTR.
- Fleming, W., & Varberg, D. E. (1989). Precalculus-wiskunde: een probleemoplossende benadering (2, geïllustreerde red.). Michigan: Prentice Hall.
- Kishan, H. (2005). Integrale calculus. Atlantic uitgevers en distributeurs.
- Purcell, E. J., Varberg, D., & Rigdon, S. E. (2007). Berekening (Negende ed.). Prentice hal.



Niemand heeft nog op dit artikel gereageerd.