De algebraïsche redenering Het bestaat in wezen uit het communiceren van een wiskundig argument via een speciale taal, waardoor het rigoureuzer en algemener wordt, door gebruik te maken van algebraïsche variabelen en bewerkingen die onderling zijn gedefinieerd. Kenmerkend voor wiskunde is de logische strengheid en abstracte neiging die in haar argumenten worden gebruikt..
Hiervoor is het nodig om de juiste "grammatica" te kennen om in dit schrijven te gebruiken. Bovendien vermijdt algebraïsch redeneren dubbelzinnigheden in de rechtvaardiging van een wiskundig argument, wat essentieel is om elk resultaat in de wiskunde te bewijzen..
Artikel index
Een algebraïsche variabele is gewoon een variabele (een letter of symbool) die een bepaald wiskundig object vertegenwoordigt..
De letters x, y, z worden bijvoorbeeld vaak gebruikt om de getallen weer te geven die aan een bepaalde vergelijking voldoen; de letters p, q r, om propositionele formules weer te geven (of hun respectievelijke hoofdletters om specifieke proposities weer te geven); en de letters A, B, X, etc., om sets te vertegenwoordigen.
De term "variabele" benadrukt dat het object in kwestie niet vaststaat, maar varieert. Dat is het geval bij een vergelijking, waarbij variabelen worden gebruikt om oplossingen te bepalen die in principe onbekend zijn.
In algemene termen kan een algebraïsche variabele worden beschouwd als een letter die een object vertegenwoordigt, of het nu vast is of niet..
Net zoals algebraïsche variabelen worden gebruikt om wiskundige objecten weer te geven, kunnen we ook symbolen beschouwen om wiskundige bewerkingen weer te geven.
Het symbool "+" staat bijvoorbeeld voor de bewerking "optellen". Andere voorbeelden zijn de verschillende symbolische notaties van logische connectieven in het geval van proposities en verzamelingen..
Een algebraïsche uitdrukking is een combinatie van algebraïsche variabelen door middel van eerder gedefinieerde bewerkingen. Voorbeelden hiervan zijn de basisbewerkingen van optellen, aftrekken, vermenigvuldigen en delen tussen getallen, of de logische connectieven in proposities en verzamelingen..
Algebraïsch redeneren is verantwoordelijk voor het uitdrukken van een wiskundige redenering of argument door middel van algebraïsche uitdrukkingen.
Deze uitdrukkingsvorm helpt om het schrijven te vereenvoudigen en af te korten, omdat het gebruik maakt van symbolische notaties en een beter begrip van redenering mogelijk maakt door het op een duidelijkere en nauwkeurigere manier weer te geven..
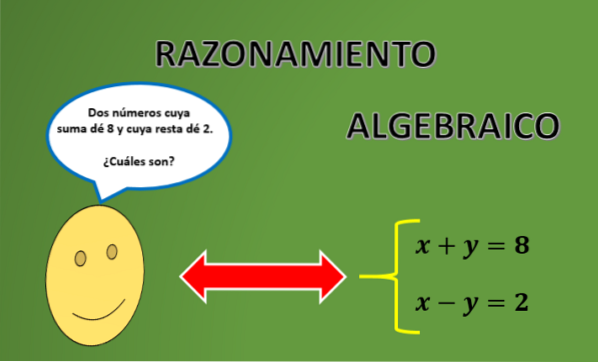
Laten we eens kijken naar enkele voorbeelden die laten zien hoe algebraïsch redeneren wordt gebruikt. Het wordt zeer regelmatig gebruikt om logica- en redeneerproblemen op te lossen, zoals we binnenkort zullen zien..
Beschouw de bekende wiskundige stelling 'de som van twee getallen is commutatief'. Laten we eens kijken hoe we deze propositie algebraïsch kunnen uitdrukken: gegeven twee getallen "a" en "b", betekent deze propositie dat a + b = b + a.
De redenering die wordt gebruikt om de oorspronkelijke propositie te interpreteren en in algebraïsche termen uit te drukken, is algebraïsche redenering..
We kunnen ook de beroemde uitdrukking 'de volgorde van de factoren verandert het product niet' noemen, die verwijst naar het feit dat het product van twee getallen ook commutatief is en algebraïsch wordt uitgedrukt als axb = bxa.
Evenzo kunnen de associatieve en distributieve eigenschappen voor optellen en product, waarin aftrekken en delen zijn inbegrepen, algebraïsch worden uitgedrukt (en in feite zijn)..
Dit type redenering omvat een zeer brede taal en wordt in veel verschillende contexten gebruikt. Afhankelijk van elk geval is het in deze contexten nodig om patronen te herkennen, zinnen te interpreteren en hun uitdrukking in algebraïsche termen te generaliseren en te formaliseren, met geldige en opeenvolgende redeneringen..
Hier volgen enkele logische problemen, die we zullen oplossen met algebraïsche redenering:
Welk getal is, als je er de helft van neemt, gelijk aan één??
Om dit type oefening op te lossen, is het erg handig om de waarde die we willen bepalen weer te geven met een variabele. In dit geval willen we een getal vinden dat, als we er de helft van nemen, als resultaat nummer één geeft. Laten we het gezochte getal met x aangeven.
"Halvering nemen" van een getal houdt in dat het door 2 wordt gedeeld. Het bovenstaande kan dus algebraïsch worden uitgedrukt als x / 2 = 1, en het probleem komt neer op het oplossen van een vergelijking, die in dit geval lineair is en heel gemakkelijk op te lossen. Oplossend voor x krijgen we dat de oplossing x = 2 is.
Concluderend, 2 is het getal dat bij het nemen van de helft gelijk is aan 1.
Hoeveel minuten tot middernacht als 10 minuten geleden 5/3 van wat er nu over is?
Laten we met "z" het aantal minuten tot middernacht aangeven (elke andere letter kan worden gebruikt). Met andere woorden, op dit moment zijn er ‘z’ minuten tot middernacht. Dit houdt in dat er 10 minuten geleden "z + 10" minuten waren om tot middernacht te gaan, en dit komt overeen met 5/3 van wat er nu ontbreekt; dat wil zeggen, (5/3) z.
Dan komt het probleem neer op het oplossen van de vergelijking z + 10 = (5/3) z. Door beide zijden van de gelijkheid met 3 te vermenigvuldigen, krijgen we de vergelijking 3z + 30 = 5z.
Als we nu de variabele "z" aan één kant van de gelijkheid groeperen, krijgen we die 2z = 15, wat inhoudt dat z = 15.
Het is dus 15 minuten voor middernacht.
In een stam die ruilhandel beoefent, zijn er deze gelijkwaardigheden:
- Een speer en een ketting worden ingeruild voor een schild.
- Een speer is gelijk aan een mes en een ketting.
- Twee schilden worden verwisseld voor drie eenheden messen.
Met hoeveel kettingen is een speer gelijk aan?
Sean:
Co = een ketting
L = een speer
E = een schild
Cu = een mes
We hebben dus de volgende relaties:
Co + L = E
L = Co + Cu
2E = 3Cu
Het probleem komt dus neer op het oplossen van een stelsel vergelijkingen. Ondanks dat er meer onbekenden dan vergelijkingen zijn, kan dit systeem worden opgelost, aangezien ze ons niet om een specifieke oplossing vragen, maar eerder een van de variabelen als functie van een andere. Wat we moeten doen is "Co" uitsluitend in termen van "L" uitdrukken.
Uit de tweede vergelijking hebben we dat Cu = L - Co. Door in de derde te substitueren, krijgen we dat E = (3L - 3Co) / 2. Ten slotte wordt door substitutie in de eerste vergelijking en vereenvoudiging verkregen dat 5Co = L; dat wil zeggen, een speer is gelijk aan vijf halskettingen.
Niemand heeft nog op dit artikel gereageerd.