
Schuine karakteristieke lijnen, vergelijkingen en voorbeelden
De schuine lijnen Het zijn degenen die hellend zijn, hetzij ten opzichte van een plat oppervlak, hetzij ten opzichte van een andere rechte lijn die een bepaalde richting aangeeft. Beschouw als voorbeeld de drie lijnen die in een vlak zijn getekend en die in de volgende afbeelding verschijnen.
We kennen hun respectievelijke relatieve posities omdat we ze vergelijken met een referentielijn, meestal de X-as aanduiding van de horizontale.
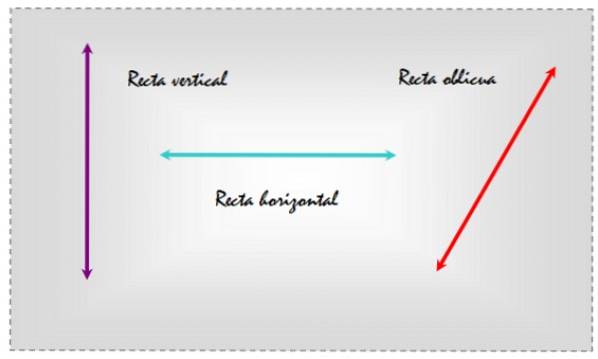
Op deze manier, door de horizontale lijn als referentie te kiezen, is de lijn aan de linkerkant verticaal, die in het midden is horizontaal en die aan de rechterkant is schuin, aangezien hij schuin staat ten opzichte van de alledaagse referentielijnen..
Nu bezetten de lijnen die zich in hetzelfde vlak bevinden, zoals het oppervlak van het papier of het scherm, een andere relatieve posities elkaar, afhankelijk van of ze elkaar kruisen of niet. In het eerste geval zijn het secanslijnen, terwijl ze in het tweede geval parallel zijn.
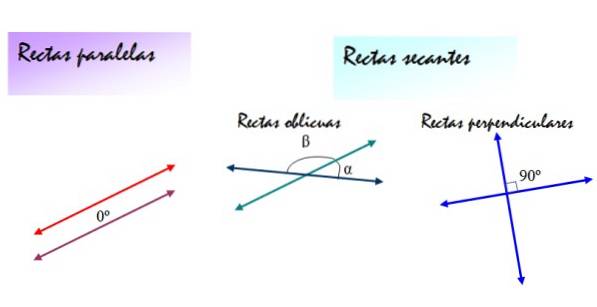
Aan de andere kant kunnen de secanslijnen schuine lijnen of loodrechte lijnen zijn. In beide gevallen zijn de hellingen van de lijnen verschillend, maar de schuine lijnen vormen hoeken α en β ertussen, verschillend van 90º, terwijl de hoeken bepaald door de loodrechte lijnen altijd 90º zijn..
De volgende afbeelding vat deze definities samen:
Artikel index
- 1 Vergelijkingen
- 1.1 Vergelijking van de lijn in het vlak
- 2 Voorbeelden van schuine lijnen
- 2.1 Lichtstralen
- 2.2 Lijnen die niet in hetzelfde vlak liggen
- 3 referenties
Vergelijkingen
Om de relatieve posities van de lijnen in het vlak te kennen, is het noodzakelijk om de hoek te kennen die ze met elkaar vormen. Merk op dat de regels zijn:
Parallel: als ze dezelfde helling hebben (dezelfde richting) en elkaar nooit snijden, zijn hun punten daarom op gelijke afstand van elkaar.
Toeval: wanneer alle punten samenvallen en dus dezelfde helling hebben, maar de afstand tussen de punten nul is.
Drogen: als hun hellingen verschillend zijn, varieert de afstand tussen hun punten en is de kruising een enkel punt.
Een manier om te weten of twee lijnen in het vlak secans of parallel zijn, is via hun helling. De criteria van parallellisme en loodrechtheid van de lijnen zijn de volgende:
Laat L twee regels zijn1 en iktwee behorend tot een vliegtuig, waarvan de hellingen respectievelijk m zijn1 en Mtwee. Deze lijnen zijn parallel als m1 = mtwee en staan loodrecht wanneer m1= -1 / mtwee
Als we de hellingen van twee lijnen in het vlak kennen en aan geen van de voorgaande criteria is voldaan, concluderen we dat de lijnen schuin zijn. Als we twee punten van een lijn kennen, wordt de helling onmiddellijk berekend, zoals we in de volgende sectie zullen zien.
Het is mogelijk om erachter te komen of twee lijnen secans of parallel zijn door hun snijpunt te vinden en het stelsel van vergelijkingen op te lossen dat ze vormen: als er een oplossing is, zijn het secans, als er geen oplossing is, zijn ze parallel, maar als de oplossingen zijn oneindig, de lijnen vallen samen.
Dit criterium informeert ons echter niet over de hoek tussen deze lijnen, zelfs niet als ze elkaar snijden.
Om de hoek tussen de lijnen te kennen, zijn twee vectoren nodig of Y v die van elk van hen zijn. Het is dus mogelijk om de hoek die ze vormen te kennen door middel van het scalaire product van de vectoren, op deze manier gedefinieerd:
ofv =u.v. cos α
Vergelijking van de lijn in het vlak
Een lijn in het cartesiaanse vlak kan op verschillende manieren worden weergegeven, zoals:
-Helling-onderscheppingsformulier: Ja m is de helling van de lijn en b is het snijpunt van de lijn met de verticale as, de vergelijking van de lijn is y = mx + b.
-Algemene vergelijking voor een rechte lijn Ax + Door + C = 0, waar m = A / B is de helling.
In het cartesiaanse vlak zijn de verticale en horizontale lijnen bijzondere gevallen van de vergelijking van de lijn.
-Verticale lijnen x = een
-Horizontale lijnen y = k
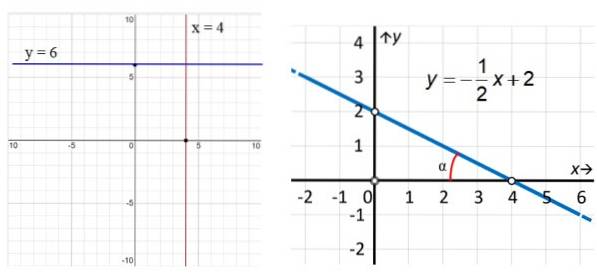
In de voorbeelden in figuur 3 heeft de verticale rode lijn vergelijking x = 4, terwijl de lijn evenwijdig aan de x-as (blauw) vergelijking y = 6 heeft. Wat betreft de lijn aan de rechterkant, zien we dat deze schuin is en naar om de vergelijking te vinden, gebruiken we de punten die in de figuur zijn gemarkeerd: (0,2) en (4,0) op deze manier:
m = (entwee - Y1) / (xtwee - X1) = (2 - 0) / (0 - 4) = - ½
De snede van deze lijn met de verticale as is y = 2, zoals te zien is in de grafiek. Met deze informatie:
y = (-½) x + 2
Het bepalen van de hellingshoek ten opzichte van de x-as is eenvoudig. Ik voel dat:
α = arctg (2/4) = 26,6º
Daarom is de positieve hoek van de x-as naar de lijn: 180º - 26,6º = 153,4º
Voorbeelden van schuine lijnen

Op veel plaatsen verschijnen schuine lijnen, het is een kwestie van opletten om ze terug te vinden in architectuur, sport, elektrische bedrading, leidingen en nog veel meer plaatsen. In de natuur zijn ook schuine lijnen aanwezig, zoals we hieronder zullen zien:
Lichtstralen
Zonlicht beweegt zich in een rechte lijn, maar de ronde vorm van de aarde beïnvloedt hoe zonlicht het oppervlak raakt..
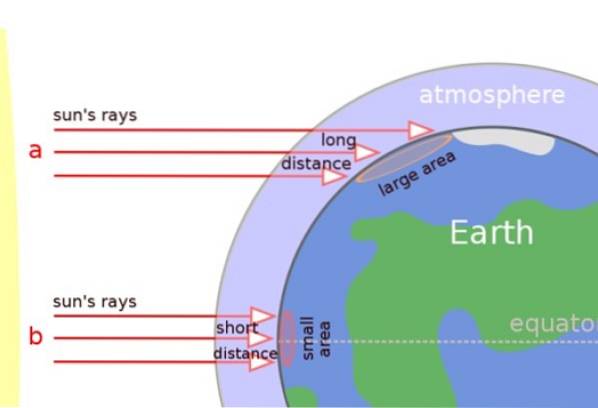
In de onderstaande afbeelding kunnen we duidelijk zien dat de zonnestralen loodrecht inslaan in tropische streken, maar in plaats daarvan schuin het oppervlak bereiken in gematigde streken en aan de polen..
Daarom leggen de zonnestralen een grotere afstand af door de atmosfeer en wordt ook de warmte over een groter oppervlak verspreid (zie figuur). Het resultaat is dat de gebieden bij de polen kouder zijn.
Lijnen die niet in hetzelfde vlak liggen
Als twee lijnen niet in hetzelfde vlak liggen, kunnen ze nog steeds schuin of kromgetrokken, zoals ze ook bekend zijn. In dit geval zijn hun richtvectoren niet parallel, maar omdat ze niet tot hetzelfde vlak behoren, snijden deze lijnen elkaar niet.
De lijnen in figuur 6 rechts staan bijvoorbeeld duidelijk op verschillende vlakken. Als je ze van bovenaf bekijkt, kun je zien dat ze elkaar inderdaad kruisen, maar dat ze geen punt gemeen hebben. Rechts zien we de wielen van de fiets, waarvan de spaken van voren gezien lijken te kruisen.

Referenties
- Geometrie. Directeur vector van een lijn. Hersteld van: juanbragado.es.
- Larson, R. 2006. Analyse met analytische meetkunde. 8e. Editie. Mcgraw heuvel.
- Wiskunde is een spel. Lijnen en hoeken. Hersteld van: juntadeandalucia.es.
- Rechte lijnen die elkaar kruisen. Hersteld van: profesoraltuna.com.
- Villena, M. analytische meetkunde in R3. Hersteld van: dspace.espol.edu.ec.



Niemand heeft nog op dit artikel gereageerd.