
Proportionaliteitsrelaties concept, voorbeelden en oefeningen
De evenredigheidsrelaties het zijn koppelingen tussen twee of meer variabelen, zodat wanneer een van de grootheden varieert, de waarde van de andere varieert. Als de ene bijvoorbeeld toeneemt, kunnen de andere toenemen of afnemen, maar in een uniforme hoeveelheid..
Oude Griekse wiskundigen realiseerden zich dat sommige variabelen op een zeer precieze manier met elkaar verband hielden. Ze realiseerden zich dat als een cirkel tweemaal de diameter van een andere is, deze een omtrek heeft die tweemaal zo lang is.

En als de diameter wordt verdrievoudigd, zal de omtrek van de omtrek ook verdrievoudigen. Dit betekent dat een vergroting van de diameter een evenredige toename van de omvang van de omtrek oplevert..
En dus kunnen we bevestigen dat de lengte van de omtrek L evenredig is met de diameter D, die als volgt wordt uitgedrukt:
L ∝ D
Waar het symbool ∝ leest "recht evenredig metOm het symbool van evenredigheid te veranderen in dat van gelijkheid en numerieke waarden op te nemen, is het nodig om het verband tussen de variabelen te bepalen, genaamd evenredigheidsconstante.
Na vele metingen te hebben gedaan, stelden de oude wiskundigen vast dat de evenredigheidsconstante tussen de grootte L van de omtrek en de diameter D ervan het getal 3,1416 was ... De ellipsen geven een oneindig aantal decimalen aan.
Deze waarde is niets anders dan het bekende getal π (pi) en op deze manier schrijven we:
L = π.D
Op deze manier is de verhouding van de lengte tot de diameter van de ene omtrek hetzelfde als de verhouding van de lengte tot de diameter van een andere. En het beste is dat we nu een manier hebben om de lengte van elke omtrek te berekenen door alleen de diameter te kennen.
Artikel index
- 1 Voorbeelden van proportionaliteitsrelaties
- 2 Directe evenredigheid en omgekeerde evenredigheid
- 3 Andere vormen van evenredigheid
- 4 oefeningen
- 4.1 - Oefening 1
- 4.2 - Oefening 2
- 5 referenties
Voorbeelden van proportionaliteitsrelaties
In de wetenschap (en ook in het dagelijks leven) is het erg belangrijk om relaties tussen variabelen te vinden, om te weten hoe veranderingen in de ene van invloed zijn op de andere. Bijvoorbeeld:
-Als je 3 kopjes bloem nodig hebt om een dozijn koekjes te maken. Hoeveel kopjes zijn er nodig om 2 en een half dozijn te maken?.
-Wetende dat een object op de planeet Mercurius 4 keer minder weegt dan op aarde, hoeveel weegt een auto van 1,5 ton dan op Mercurius??
-Hoe beïnvloedt de verandering in de uitgeoefende kracht de versnelling van het lichaam waarop deze wordt uitgeoefend??
-Als een voertuig met een uniforme rechtlijnige beweging op een snelweg rijdt en we weten dat het 30 km aflegt in 10 minuten, wat is dan de afgelegde afstand na 20 minuten??
-Als we een draad hebben waar een elektrische stroom doorheen gaat, hoe varieert de spanning dan tussen de uiteinden als deze toeneemt?
-Als de diameter van een cirkel wordt verdubbeld, hoe wordt het oppervlak dan beïnvloed??
-Hoe beïnvloedt afstand de intensiteit van het elektrische veld dat wordt geproduceerd door een puntlading?
Het antwoord ligt in proportionaliteitsrelaties, maar niet alle relaties zijn van hetzelfde type. Dan vinden we ze voor alle situaties die hier aan de orde zijn.
Directe evenredigheid en omgekeerde evenredigheid
Twee variabelen x en y zijn in directe verhouding als ze gerelateerd zijn door:
y = kx
Waar k de evenredigheidsconstante is. Een voorbeeld is de relatie tussen de hoeveelheden bloem en koekjes. Als we deze variabelen in kaart brengen, krijgen we een rechte lijn zoals in de afbeelding:
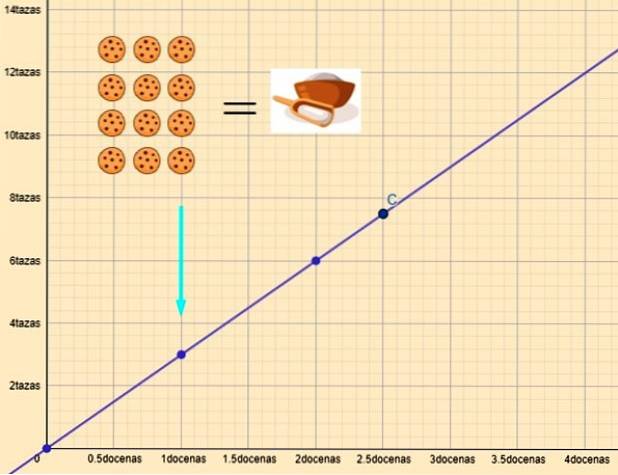
Als y de kopjes bloem zijn en x de dozijn koekjes zijn, is de relatie tussen beide:
y = 3x
Voor x = 1 dozijn hebben we y = 3 kopjes bloem nodig. En voor x = 2,5 dozijn, is y = 7,5 kopjes bloem vereist.
Maar we hebben ook:
-Versnelling naar die een lichaam ervaart, is evenredig met de kracht F. erop inwerken, zijnde de massa van het lichaam, genoemd m, de evenredigheidsconstante:
F. = mnaar
Daarom, hoe groter de uitgeoefende kracht, hoe groter de geproduceerde versnelling..
-In ohmse geleiders is de spanning V tussen hun uiteinden evenredig met de stroom die ik heb toegepast. De evenredigheidsconstante is de weerstand R van de geleider:
V = RI
-Wanneer een object met een uniforme rechtlijnige beweging beweegt, is de afstand d is evenredig met de tijd t, zijnde de snelheid v de evenredigheidsconstante:
d = ww
Soms vinden we twee grootheden zodat een toename van één een verminderen proportioneel in de andere. Deze afhankelijkheid wordt genoemd omgekeerde verhouding.
In de vorige vergelijking is bijvoorbeeld de tijd t die nodig is om een bepaalde afstand d af te leggen, omgekeerd evenredig met de snelheid v van de reis:
t = d / v
En zo hoger is de snelheid v, minder tijd die de auto nodig heeft om de afstand af te leggen d. Als bijvoorbeeld de snelheid wordt verdubbeld, wordt de tijd gehalveerd.
Als twee variabelen x en y in omgekeerde proportie zijn, kunnen we schrijven:
y = k / x
K de constante van evenredigheid zijn. De grafiek van deze afhankelijkheid is:
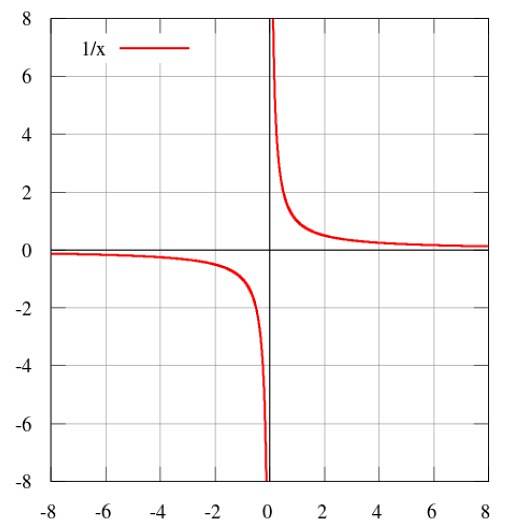
Andere vormen van evenredigheid
In een van de eerder genoemde voorbeelden vroegen we ons af wat er met de oppervlakte van de cirkel gebeurt als de straal toeneemt. Het antwoord is dat het gebied recht evenredig is met het kwadraat van de straal, waarbij π de evenredigheidsconstante is:
A = πRtwee
Als de straal wordt verdubbeld, neemt het gebied toe met een factor 4.
En in het geval van het elektrische veld EN geproduceerd door een puntlading wat, het is bekend dat de intensiteit afneemt met het omgekeerde van het kwadraat van de afstand r aan de lading wat
E = ken q / rtwee
Maar we kunnen ook stellen dat de intensiteit van het veld recht evenredig is met de grootte van de lading, zijnde de evenredigheidsconstante ken, de elektrostatische constante.
Andere proportionaliteiten die ook in Science worden gepresenteerd, zijn exponentiële proportionaliteit en logaritmische proportionaliteit. In het eerste geval zijn de variabelen x en y gerelateerd aan:
y = k.aX
Waar a de basis is, een positief getal anders dan 0, meestal 10 of het getal e. De exponentiële groei van bacteriën heeft bijvoorbeeld deze vorm.
In het tweede geval is de relatie tussen de variabelen:
y = k.lognaar X
Opnieuw is a de basis van de logaritme, die vaak 10 (decimale logaritme) of e (natuurlijke logaritme) is.
Opleiding
- Oefening 1
Wetende dat een object op de planeet Mercurius 4 keer minder weegt dan op aarde, hoeveel zou een auto van 1,5 ton dan op Mercurius wegen??
Oplossing
Gewicht op kwik = (1/4) Gewicht op aarde = (1/4) x 1,5 ton = 0,375 ton.
- Oefening 2
Voor een feestje besluiten sommige vrienden sap te maken van fruitconcentraat. De instructies op de verpakking zeggen dat één glas concentraat 15 glazen sap kan maken. Hoeveel concentraat is er nodig om 110 glazen sap te maken?
Oplossing
Laat y het aantal glazen sap zijn en x het aantal glazen concentraat. Ze zijn gerelateerd door:
y = kx
Door de waarden y = 15 en x = 1 te vervangen, wordt de constante k opgelost:
k = y / x = 15/1 = 15
Daarom:
110 = 15 x
x = 110/15 = 7,33 glazen fruitconcentraat.
Referenties
- Baldor, A. 1974. Algebra. Culturele Venezolana S.A.
- Giancoli, D. 2006. Natuurkunde: principes met toepassingen. 6e. Ed Prentice Hall.
- Varsity-docenten. Proportionaliteitsrelaties. Hersteld van: varsitytutors.com
- Wikipedia. Evenredigheid Hersteld van: es.wikipedia.org.
- Zill, D. 1984. Algebra en trigonometrie. Mcgraw heuvel.


Niemand heeft nog op dit artikel gereageerd.