De vector aftrekken of vectoraftrekking tussen vectoren of Y v aangegeven door of - v, wordt berekend door de vector op te tellen of met de vector er tegenover v. Algebraïsch wordt de aftrekking als volgt uitgedrukt:
of - v of + -v
Het is mogelijk om vectoraftrekking uit te voeren volgens verschillende procedures, bijvoorbeeld grafisch, op deze manier een vector v wordt getekend door een georiënteerd lijnsegment - een pijl-.
De lengte van de pijl komt overeen met de module van de vector, de helling - ten opzichte van een gegeven referentielijn - geeft de richting aan en het uiteinde geeft de richting van de vector aan.
De vector tegenover v het heeft dezelfde lengte en richting, maar in tegengestelde richting. Vervolgens, voordat u de aftrekking tussen of Y v, het is noodzakelijk om de tegenovergestelde vector te tekenen v, en voeg deze vector toe aan u.
Het is erg belangrijk op te merken dat vectoraftrekking niet commutatief is, dat wil zeggen dat de volgorde van de vectoren het resultaat verandert, daarom:
of - v v - of
De grafische procedure kan worden uitgevoerd met behulp van een van deze methoden, waarvan we de stappen hieronder zullen uitleggen:
-Driehoeksmethode.
-Parallellogram-methode.
Artikel index
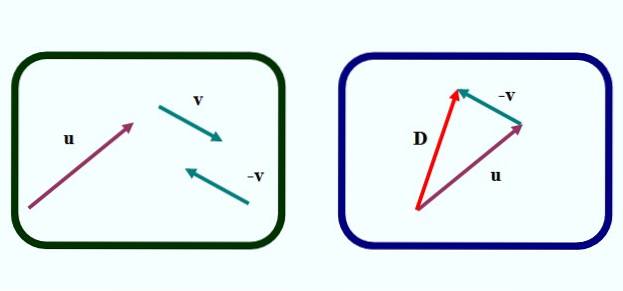
In figuur 1 hebben we de eerste van de methoden om twee vectoren grafisch af te trekken. Het gaat over driehoek methode, omdat de figuur die wordt gevormd door het vaststellen van de vectoren een driehoek is, zoals we in de linker afbeelding kunnen zien.
Om het aftrekken te doen of - v we gaan als volgt te werk:
-Teken de vector -v van vector v, door vertaling met een liniaal en vierkant, maar de richting van de pijl veranderen (afbeelding links).
-Gaat naar vector -v zodanig dat zijn oorsprong samenvalt met het einde van de vector of (rechter afbeelding).
-Vervolgens wordt een vector getekend (in rood in de rechter afbeelding) die uitgaat van de oorsprong van of tot het einde van v. Bel D y is de verschilvector:
D of - v
Bij de parallellogrammethode moeten de vectoren die moeten worden opgeteld of afgetrokken, samenvallen op hun oorsprongspunten. Stel dat we willen vinden of - v Met onze vectoren hierboven weergegeven, zijn de stappen om het aftrekken van vectoren met deze methode te vinden als volgt:
-Bepaal de tegenoverliggende vector v, Wat is het -v, zoals hierboven beschreven voor de driehoeksmethode.
-Vertaal vectoren zorgvuldig of Y -v op zo'n manier dat hun oorsprong samenvalt.
-Nu worden gesegmenteerde parallelle lijnen getekend vanaf de uiteinden van elke vector. De figuur die wordt gevormd is een parallellogram en in speciale gevallen waarin de vectoren loodrecht staan, resulteert een rechthoek of een vierkant..
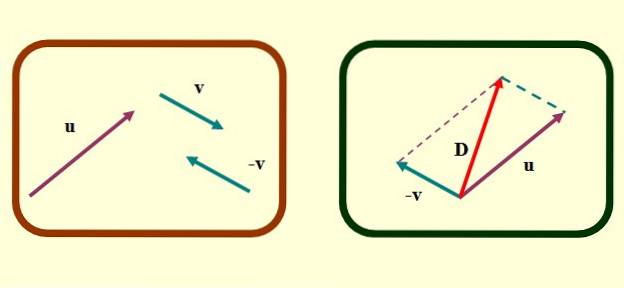
-Ten slotte wordt een vector getekend die vertrekt vanuit de gemeenschappelijke oorsprong van of Y v tot het uiterste waar de gesegmenteerde parallelle lijnen elkaar kruisen. Dit is de vector D of aftrekken.
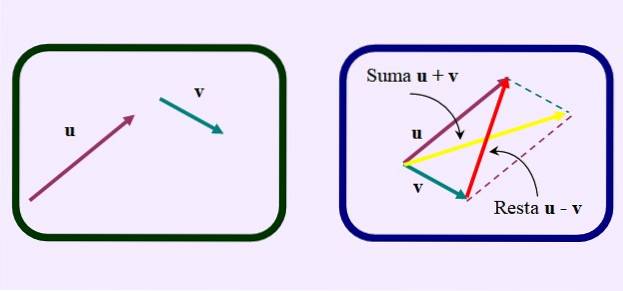
Een andere manier om de aftrekking uit te voeren, is door het parallellogram te tekenen alsof u de vectoren wilt optellen.
Maar in plaats van de gebruikelijke diagonaal van de som te tekenen, die van de gemeenschappelijke oorsprong naar het snijpunt van de parallellen gaat, tegenovergestelde of kortere diagonaal, zoals te zien in de figuur:
Een schip vaart op een rivier en doet dat in tegengestelde richting van de stroming. Een waarnemer op het land merkt op dat de snelheid van de boot wordt verminderd door de werking van de stroming.
De snelheid is een vector en in dit voorbeeld wijst de snelheid van de boot in één richting en heeft de snelheid van de stroming dezelfde richting en tegengestelde richting. De netto snelheid van het schip is de som van beide vectoren.
Als de instrumenten van de boot bijvoorbeeld aangeven dat hij vaart met v '= + 40 km / u en een waarnemer aan de kust meet dat de boot vaart met v = + 30 km / u. Aangezien v = v '+ Vc, waarbij Vc de snelheid van de stroom is die wordt berekend door de snelheden v en v' respectievelijk af te trekken: Vc = v - v '= 30 km / h - 40 km / h = -10 km / h.
In kinematica hebben we belangrijke vectoren die veranderingen beschrijven:
-Offset voor positieveranderingen.
-Gemiddelde snelheid, om te kwantificeren hoe snel de positie in de loop van de tijd varieert.
-Acceleratie, voor snelheidsveranderingen als functie van de tijd.
De verplaatsingsvector beschrijft de positieverandering die een lichaam ervaart tijdens zijn beweging.
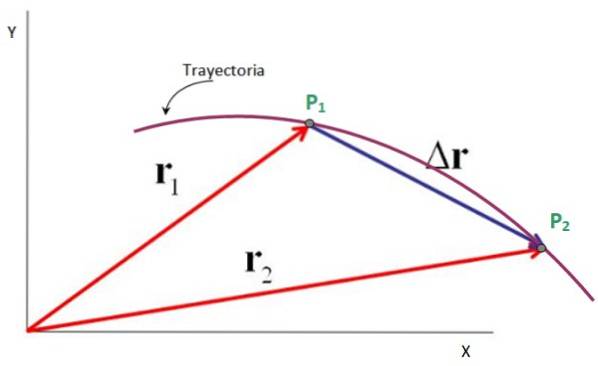
Laten we bijvoorbeeld eens kijken naar een deeltje dat het vlakke pad beschrijft dat in de figuur wordt getoond, waarin het van punt P passeert1 om P te wijzentwee.
De vectoren die vanaf de oorsprong van het x-y-coördinatensysteem naar deze punten zijn gericht, zijn de positievectoren r1 Y rtwee, terwijl de verplaatsingsvector Δ isr, dat gaat van P1 tot Ptwee. Is het waar dat:
Δr rtwee - r1
Daarom is de verplaatsingsvector de aftrekking tussen de eindpositievector en de beginpositievector, zoals weergegeven in de volgende afbeelding. De eenheden zijn ook die van de positie: meters, voet, mijlen, centimeters en meer..
Van zijn kant, de gemiddelde snelheidsvector vm wordt gedefinieerd als de offset vermenigvuldigd met de inverse van het tijdsinterval:
Een deeltje dat een cirkel beschrijft, heeft 5 seconden nodig om van punt A naar punt B te gaan. Bij A heeft het een snelheid vNAAR = 60 km / u naar de + x-as toe en bij B is vB. = 60 km / u richting + y. Bepaal grafisch en analytisch de gemiddelde versnelling.
In grafische vorm worden richting en richting van de gemiddelde versnelling bepaald door:
In de volgende afbeelding is de aftrekking vB. - vNAAR, met behulp van de driehoeksmethode, aangezien de gemiddelde versnelling naarm is evenredig met Δv. De gevormde driehoek heeft de twee benen gelijk en daarom zijn de scherpe binnenhoeken elk 45º..
Analytisch, als de + x-richting samenvalt met de eenheidsvector ik en de + y richting met de eenheidsvector j, dan:
Δv = 60 km / u j - 60 km / u ik
Bij Δt = 5 s, volgens de informatie in de verklaring, is de gemiddelde versnelling:
naarm = (60 km / u j - 60 km / u ik) / 5 seconden 12 (j-ik) km / (uur)
Niemand heeft nog op dit artikel gereageerd.