
Axiale symmetrie-eigenschappen, voorbeelden en oefeningen
De axiale symmetrie Het treedt op wanneer de punten van een figuur samenvallen met de punten van een andere figuur door middel van een rechte middelloodlijn die de symmetrieas wordt genoemd. Het wordt ook wel radiale, roterende of cilindrische symmetrie genoemd..
Het wordt meestal toegepast in geometrische figuren, maar het is gemakkelijk waarneembaar in de natuur, aangezien er dieren zijn zoals vlinders, schorpioenen, lieveheersbeestjes of mensen die axiale symmetrie vertonen..

Artikel index
- 1 Hoe de axiale symmetrie te vinden
- 2 Eigenschappen van axiale symmetrie
- 3 Voorbeelden van axiale symmetrie
- 4 Axiale symmetrieoefeningen
- 4.1 Oefening 1
- 4.2 Oefening 2
- 4.3 Oefening 3
- 4.4 Oefening 4
- 5 referenties
Hoe axiaal symmetrisch te vinden
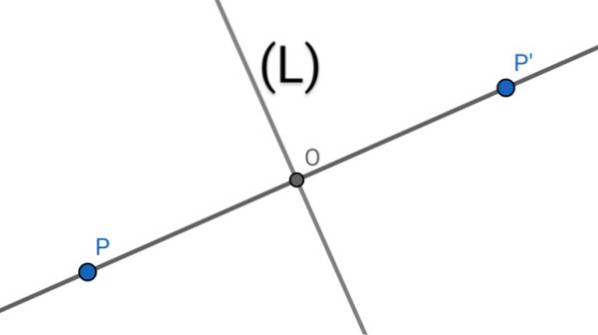
Om de axiale symmetrie P 'van een punt P te vinden ten opzichte van een lijn (L), worden de volgende geometrische bewerkingen uitgevoerd:
1. - De loodlijn op de lijn (L) die door punt P loopt, wordt getekend.
2.- Het onderscheppen van de twee lijnen bepaalt een punt O.
3.- De lengte van het segment PO wordt gemeten, vervolgens wordt deze lengte over de lijn (PO) gekopieerd, beginnend bij O in de richting van P naar O, waarbij het punt P 'wordt bepaald.
4.- Punt P 'is de axiale symmetrie van punt P ten opzichte van de as (L), aangezien de lijn (L) de middelste is van het segment PP', waarbij O het middelpunt van dat segment is.
Eigenschappen van axiale symmetrie
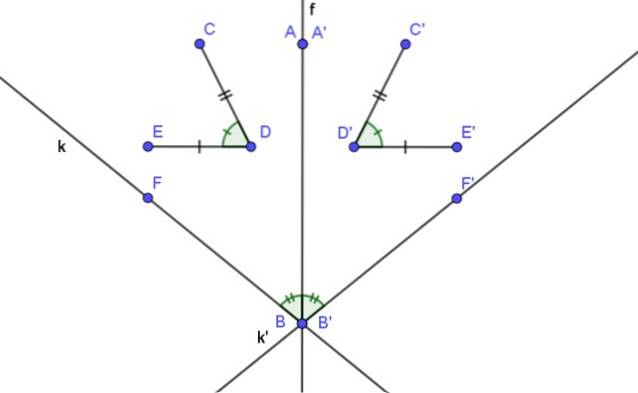
- Axiale symmetrie is isometrisch, dat wil zeggen dat de afstanden van een geometrische figuur en de bijbehorende symmetrie behouden blijven.
- De maat van een hoek en die van zijn symmetrie zijn gelijk.
- De axiale symmetrie van een punt op de symmetrieas is het punt zelf.
- De symmetrische lijn van een lijn evenwijdig aan de symmetrieas is ook een lijn evenwijdig aan genoemde as.
- Een secanslijn ten opzichte van de symmetrieas heeft als symmetrische lijn een andere secanslijn die op zijn beurt de symmetrieas snijdt op hetzelfde punt van de oorspronkelijke lijn.
- Het symmetrische beeld van een lijn is een andere lijn die een hoek vormt met de symmetrieas van dezelfde maat als die van de originele lijn.
- Het symmetrische beeld van een lijn loodrecht op de symmetrieas is een andere lijn die de eerste overlapt.
- Een lijn en zijn axiale symmetrische lijn vormen een hoek waarvan de middelloodlijn de symmetrieas is.
Voorbeelden van axiale symmetrie
De natuur vertoont talloze voorbeelden van axiale symmetrie. U kunt bijvoorbeeld de symmetrie zien van gezichten, insecten zoals vlinders, de weerspiegeling op kalme wateroppervlakken en spiegels of de bladeren van planten, en vele anderen..


Axiale symmetrie-oefeningen
Oefening 1
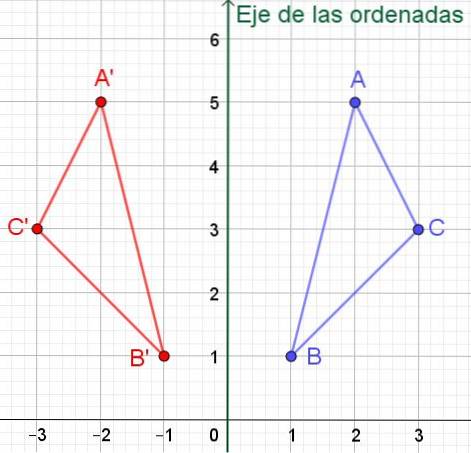
We hebben de driehoek van hoekpunten A, B en C waarvan de Cartesiaanse coördinaten respectievelijk A = (2, 5), B = (1, 1) en C = (3,3) zijn. Vind de Cartesiaanse coördinaten van de driehoek symmetrisch rond de Y-as (ordinaat-as).
Oplossing: Als een punt P coördinaten (x, y) heeft, dan is de symmetrie rond de ordinaatas (Y-as) P '= (- x, y). Dat wil zeggen, de waarde van zijn abscis verandert van teken, terwijl de waarde van de ordinaat hetzelfde blijft.
In dit geval heeft de symmetrische driehoek met hoekpunten A ', B' en C 'coördinaten:
A '= (- 2, 5); B '= (- 1, 1) en C' = (- 3, 3) zoals te zien is in figuur 6.
Oefening 2
Verwijzend naar driehoek ABC en zijn symmetrische A'B'C 'uit oefening 1, controleer of de corresponderende zijden van de originele driehoek en zijn symmetrische driehoek dezelfde lengte hebben.
Oplossing: Om de afstand of lengte van de zijden te vinden, gebruiken we de Euclidische afstandsformule:
d (A, B) = √ ((Bx - Ax) ^ 2 + (Door - Ay) ^ 2) = √ ((1-2) ^ 2 + (1-5) ^ 2) = √ ((- 1 ) ^ 2 + (-4) ^ 2) = √ (17) = 4.123
De lengte van de overeenkomstige symmetrische zijde A'B 'wordt hieronder berekend:
d (A ', B') = √ ((Bx'-Ax ') ^ 2 + (By'-Ay') ^ 2) = √ ((- 1 + 2) ^ 2 + (1-5) ^ 2 ) = √ ((1) ^ 2 + (-4) ^ 2) = √ (17) = 4.123
Op deze manier wordt geverifieerd dat axiale symmetrie de afstand tussen twee punten behoudt. De procedure kan worden herhaald voor de andere twee zijden van de driehoek en zijn symmetrisch om de onveranderlijkheid in lengte te controleren. Bijvoorbeeld | AC | = | A'C '| = √5 = 2.236.
Oefening 3
Controleer met betrekking tot driehoek ABC en zijn symmetrische A'B'C 'uit oefening 1 of de corresponderende hoeken van de originele driehoek en zijn symmetrische driehoek dezelfde hoekmaat hebben.
Oplossing: Om de maten van de hoeken BAC en B'A'C 'te bepalen, wordt eerst het scalaire product van de vectoren berekend AB met AC en dan het puntproduct van A'B ' met A'C '.
Onthoud dat:
A = (2, 5), B = (1, 1) en C = (3,3)
A '= (- 2, 5); B '= (- 1, 1) en C' = (- 3, 3).
Het heeft:
AB <1-2, 1-5> Y AC <3-2, 3-5>
op dezelfde manier
A'B ' <-1+2, 1-5> Y AC <-3+2, 3-5>
Dan worden de volgende scalaire producten gevonden:
AB⋅AC <-1, -4><1, -2> = -1⋅1 + (-4) ⋅ (-2) = -1 + 8 = 7
Evenzo
A'B'⋅A'C ' <1, -4><-1, -2> = 1⋅ (-1) + (-4) ⋅ (-2) = -1 + 8 = 7
De maat van de hoek BAC is:
∡BAC = ArcCos ( AB⋅AC AB | |AC |
ArcCos (7 / (4.123⋅2.236)) = 40,6º
Evenzo is de maat van hoek B'A'C ':
∡B'A'C '= ArcCos ( A'B'⋅A'C ' A'B '| |A'C '|
ArcCos (7 / (4.123⋅2.236)) = 40,6º
Concluderend dat axiale symmetrie de hoekmaat behoudt.
Oefening 4
Laat een punt P van coördinaten zijn (a, b). Zoek de coördinaten van zijn axiale symmetrie P 'ten opzichte van de lijn y = x.
Oplossing: We noemen (a ', b') de coördinaten van het symmetrische punt P 'ten opzichte van de rechte y = x. Het middelpunt M van het segment PP 'heeft coördinaten ((a + a') / 2, (b + b ') / 2) en bevindt zich ook op de lijn y = x, dus de volgende gelijkheid is waar:
a + a '= b + b'
Aan de andere kant heeft het segment PP 'helling -1 omdat het loodrecht staat op de lijn y = x met helling 1, dus de volgende gelijkheid geldt:
b - b '= a' -a
Oplossend voor de twee voorgaande gelijkheden a 'en b' wordt geconcludeerd dat:
a '= b en dat b' = a.
Dat wil zeggen, gegeven een punt P (a, b), de axiale symmetrie ten opzichte van de lijn y = x is P '(b, a).
Referenties
- Arce M., Blázquez S en anderen. Transformaties van het vliegtuig. Hersteld van: educutmxli.files.wordpress.com
- Berekening cc. Axiale symmetrie. Hersteld van: calculo.cc
- Superprof. Axiale symmetrie. Hersteld van: superprof.es
- Wikipedia. Axiale symmetrie. Hersteld van: es.wikipedia.com
- Wikipedia. Circulaire symmetrie. Hersteld van: en.wikipedia.com



Niemand heeft nog op dit artikel gereageerd.