De Bestaan en uniciteit stelling stelt de noodzakelijke en voldoende voorwaarden vast zodat een differentiaalvergelijking van de eerste orde, met een gegeven beginvoorwaarde, een oplossing heeft en dat deze oplossing ook de enige is.
De stelling geeft echter geen enkele techniek of indicatie hoe een dergelijke oplossing te vinden. De existentie- en uniciteitsstelling wordt ook uitgebreid tot differentiaalvergelijkingen van hogere orde met beginvoorwaarden, die bekend staan als het Cauchy-probleem..
De formele verklaring van de existentie- en uniciteitsstelling is als volgt:
'Voor een differentiaalvergelijking y '(x) = f (x, y) met beginvoorwaarde y (a) = b, bestaat ten minste één oplossing in een rechthoekig gebied van het vlak XY met to the point (a, b), Ja f (x, y) het is continu in die regio. En als de partiële afgeleide van F. met betrekking tot Y: g = ∂f / ∂en is continu in hetzelfde rechthoekige gebied, dan is de oplossing uniek in een buurt van het punt (a, b) content in de continuïteitsregio van F. Y g.
Het nut van deze stelling ligt ten eerste in het weten in welke gebieden van het XY-vlak een oplossing kan bestaan en ook in het weten of de gevonden oplossing de enige mogelijke is of dat er andere zijn..
Merk op dat in het geval dat niet aan de uniciteitsvoorwaarde wordt voldaan, de stelling niet kan voorspellen hoeveel oplossingen in totaal het Cauchy-probleem heeft: misschien is het een, twee of meer.
Artikel index
Voor deze stelling zijn twee mogelijke bewijzen bekend, een daarvan is het bewijs van Charles Émile Picard (1856-1941) en de andere is te danken aan Giuseppe Peano (1858-1932) gebaseerd op het werk van Augustin Louis Cauchy (1789-1857) ).
Het is opmerkelijk dat de meest briljante wiskundige geesten van de negentiende eeuw deelnamen aan het bewijs van deze stelling, dus het kan worden aangenomen dat geen van beide eenvoudig is..
Om de stelling formeel te bewijzen, is het noodzakelijk om eerst een reeks meer geavanceerde wiskundige concepten vast te stellen, zoals Lipschitz-achtige functies, Banachruimten, de existentiestelling van Carathéodory en verschillende andere, die buiten het bestek van het artikel vallen..
Een groot deel van de differentiaalvergelijkingen die in de natuurkunde worden behandeld, hebben te maken met continue functies in de interessegebieden, daarom zullen we ons beperken tot het laten zien hoe de stelling wordt toegepast in eenvoudige vergelijkingen..
Laten we de volgende differentiaalvergelijking bekijken met een beginvoorwaarde:
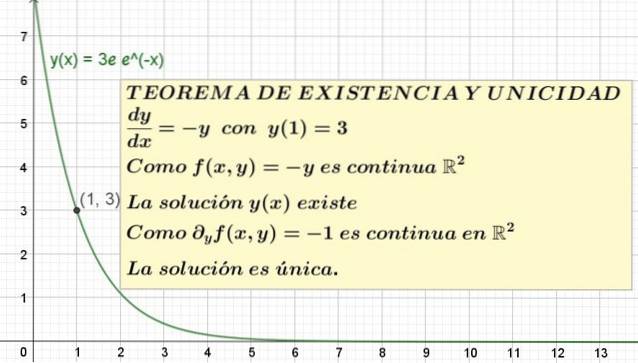
y '(x) = - y; met y (1) = 3
Is er een oplossing voor dit probleem? Is het de enige mogelijke oplossing?
In de eerste plaats wordt geëvalueerd of de oplossing van de differentiaalvergelijking bestaat en dat deze ook aan de beginvoorwaarde voldoet.
In dit voorbeeld f (x, y) = - y de conditie van het bestaan vereist weten of f (x, y) is continu in een gebied van het vliegtuig XY dat het coördinatenpunt x = 1, y = 3 bevat.
Maar f (x, y) = - y is de affiene functie, die continu is op het gebied van reële getallen en bestaat in het hele bereik van reële getallen.
Daarom wordt geconcludeerd dat f (x, y) continu is in Rtwee, dus de stelling garandeert het bestaan van ten minste één oplossing.
Dit wetende, is het noodzakelijk om te evalueren of de oplossing uniek is of dat er integendeel meer dan één is. Hiervoor is het nodig om de partiële afgeleide van te berekenen F. met betrekking tot de variabele Y
∂f / ∂y = ∂ (-y) / ∂y = -1
Dan g (x, y) = -1 wat een constante functie is, die ook voor alle R is gedefinieerdtwee en het is ook daar continu. Hieruit volgt dat de existentie- en uniciteitsstelling garandeert dat dit initiële-waardeprobleem een unieke oplossing heeft, hoewel het ons niet vertelt wat het is..
Beschouw de volgende gewone differentiaalvergelijking van de eerste orde met beginvoorwaarde:
y '(x) = 2√y; y (0) = 0.
Is er een oplossing? y (x) voor dit probleem? Zo ja, bepaal dan of er een of meer is.
We kijken naar de functie f (x, y) = 2√y. De functie F. is alleen gedefinieerd voor y≥0, aangezien we weten dat een negatief getal geen echte wortel heeft. Bovendien f (x, y) is continu in het bovenste halve vlak van Rtwee inclusief de X-as, dus het bestaan en de uniciteit stelling garandeert ten minste één oplossing in die regio.
Nu bevindt de beginvoorwaarde x = 0, y = 0 zich aan de rand van het oplossingsgebied. Vervolgens nemen we de partiële afgeleide van f (x, y) met betrekking tot y:
∂f/ ∂y = 1 / √y
In dit geval is de functie niet gedefinieerd voor y = 0, precies waar de beginvoorwaarde is.
Wat zegt de stelling ons? Het vertelt ons dat hoewel we weten dat er ten minste één oplossing is, het bovenste halve vlak van de X-as inclusief de X-as, aangezien niet aan de uniciteitsvoorwaarde is voldaan, er geen garantie is dat er een unieke oplossing zal zijn.
Dit betekent dat er een of meer oplossingen kunnen zijn in het gebied van continuïteit van f (x, y). En zoals altijd vertelt de stelling ons niet wat ze zouden kunnen zijn.
Los het Cauchy-probleem op in Voorbeeld 1:
y '(x) = - y; met y (1) = 3.
Zoek de functie y (x) die voldoet aan de differentiaalvergelijking en de beginvoorwaarde.
In Voorbeeld 1 is vastgesteld dat dit probleem een oplossing heeft en ook uniek is. Om de oplossing te vinden, moet allereerst worden opgemerkt dat het een differentiaalvergelijking is van de eerste graad van scheidbare variabelen, die als volgt wordt geschreven:
dy / dx = - y → dy = -y dx
Verdelen tussen en in beide leden om de variabelen te scheiden die we hebben:
dy / y = - dx
De onbepaalde integraal wordt toegepast in beide leden:
∫ (1 / y) dy = - ∫dx
Het oplossen van de onbepaalde integralen die we hebben:
ln (y) = -x + C
waarbij C een integratieconstante is die wordt bepaald door de beginvoorwaarde:
ln (3) = -1 + C, dat wil zeggen C = 1 + ln (3)
Het vervangen van de waarde van C en het herschikken blijft:
ln (y) - ln (3) = -x + 1
De volgende eigenschap van logaritmen toepassen:
Het verschil in logaritmen is de logaritme van het quotiënt
De bovenstaande uitdrukking kan als volgt worden herschreven:
ln (y / 3) = 1 - x
De exponentiële functie met grondtal e in beide leden wordt toegepast om te verkrijgen:
y / 3 = e(1 - x)
Wat gelijk staat aan:
y = 3e e-X
Dit is de unieke oplossing van de vergelijking y '= -y met y (1) = 3. De grafiek van deze oplossing is weergegeven in figuur 1.
Zoek twee oplossingen voor het probleem in voorbeeld 2:
y '(x) = 2√ (y); y (0) = 0.
Het is ook een vergelijking van scheidbare variabelen, die er, geschreven in differentiële vorm, er als volgt uitziet:
dy / √ (y) = 2 dx
Het nemen van de onbepaalde integraal in beide leden blijft:
twee √ (y) = 2 x + C
Hoe weet je dat y≥0 in de oplossingsregio hebben we:
y = (x + C)twee
Maar aangezien aan de beginvoorwaarde x = 0, y = 0 moet zijn voldaan, is de constante C nul en blijft de volgende oplossing over:
y (x) = xtwee.
Maar deze oplossing is niet uniek, de functie y (x) = 0 is ook een oplossing voor het gestelde probleem. De existentie- en uniciteitsstelling die in Voorbeeld 2 op dit probleem werd toegepast, had al voorspeld dat er meer dan één oplossing zou kunnen zijn.
Niemand heeft nog op dit artikel gereageerd.