De De stelling van Green is een berekeningsmethode die wordt gebruikt om lijnintegralen te relateren aan dubbele oppervlakte- of oppervlakte-integralen. De betrokken functies moeten worden aangeduid als vectorvelden en gedefinieerd binnen het pad C.
Een regelintegraal-uitdrukking kan bijvoorbeeld erg moeilijk op te lossen zijn; door de stelling van Green te implementeren, worden dubbele integralen echter vrij basaal. Het is altijd belangrijk om de positieve richting van het traject te respecteren, dit verwijst naar de richting tegen de klok in.
De stelling van Green is een specifiek geval van de stelling van Stokes, waarbij de projectie van de vectorfunctie wordt uitgevoerd in het xy-vlak.
Artikel index
De uitdrukking van de stelling van Green is als volgt:
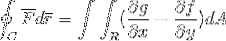
De eerste term toont de lijnintegraal gedefinieerd door het pad "C", van het scalaire product tussen de vectorfunctie "F" en die van de vector "r".
C: Het is het gedefinieerde pad waarop de vectorfunctie zal worden geprojecteerd zolang het voor dat vlak is gedefinieerd.
F: Vectorfunctie, waarbij elk van zijn componenten wordt gedefinieerd door een dergelijke functie (f, g).
r: Het is een vector die raakt aan het gebied R waarover de integraal wordt gedefinieerd. In dit geval werken we met een differentieel van deze vector.
In de tweede term zien we de stelling van Green ontwikkeld, waarbij de dubbele integraal gedefinieerd in het gebied R van het verschil van de partiële afgeleiden van g en f, met betrekking tot respectievelijk x en y, wordt waargenomen. Door een oppervlakteverschil dat niets meer is dan het product van beide tweedimensionale verschillen (dx.dy).
Deze stelling is perfect toepasbaar voor ruimte- en oppervlakte-integralen.
Om de stelling van Green op een eenvoudige manier te bewijzen, wordt deze taak opgesplitst in 2 delen. We gaan er eerst van uit dat de vectorfunctie F alleen een definitie heeft in de versor ik. Terwijl de functie "g" overeenkomt met de versor j zal gelijk zijn aan nul.
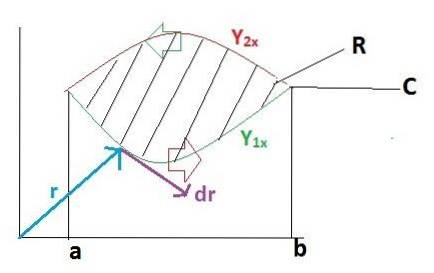
F = f (x, y)ik + g (x, y)j = f (x, y)ik + 0
r = xik + Yj
dr = dxik + dyj
Eerst ontwikkelen we de lijnintegraal over het traject C, waarvoor het traject gesectoriseerd is in 2 secties die eerst van a naar b gaan en dan van b naar a.
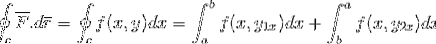
De definitie van de fundamentele stelling van calculus wordt toegepast voor een bepaalde integraal.
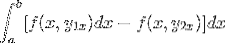
De uitdrukking wordt opnieuw geordend tot een enkele integraal, het negatief wordt een gemeenschappelijke factor gemaakt en de volgorde van de factoren wordt omgekeerd.
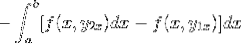
Als we deze uitdrukking in detail bekijken, wordt het duidelijk dat wanneer we de primitieve functiecriteria toepassen, we in de aanwezigheid zijn van de integraal van de uitdrukking afgeleid van f met betrekking tot y. Geëvalueerd in parameters
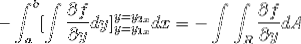
Nu is het voldoende om te veronderstellen dat de vectorfunctie F alleen is gedefinieerd voor g (x, y)j. Waar bij gebruik op een manier die vergelijkbaar is met het vorige geval, wordt het volgende verkregen:
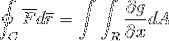
Om te eindigen, worden de 2 bewijzen genomen en samengevoegd in het geval dat de vectorfunctie waarden aanneemt voor beide versores. Op deze manier wordt getoond hoe de lijnintegraal na te zijn gedefinieerd en beschouwd als een eendimensionaal traject, volledig kan worden ontwikkeld voor het vlak en de ruimte.
F = f (x, y)ik + g (x, y)j
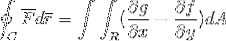
Op deze manier wordt de stelling van Green bewezen.
De toepassingen van de stelling van Green zijn breed in de takken van natuurkunde en wiskunde. Deze strekken zich uit tot elke toepassing of gebruik dat kan worden gegeven aan lijnintegratie.
Het mechanische werk gedaan door een kracht F door een pad C, kan worden ontwikkeld door een lijnintegraal die wordt uitgedrukt als een dubbele integraal van een gebied door middel van de stelling van Green.
De traagheidsmomenten van veel lichamen die worden blootgesteld aan externe krachten op verschillende toepassingspunten, reageren ook op lijnintegralen die kunnen worden ontwikkeld met de stelling van Green..
Dit heeft meerdere functionaliteiten in de resistentiestudies van gebruikte materialen. Waar externe waarden kunnen worden gekwantificeerd en meegewogen voorafgaand aan de uitwerking van verschillende elementen.
Over het algemeen vergemakkelijkt de stelling van Green het begrip en de definitie van de gebieden waar vectorfuncties worden gedefinieerd met betrekking tot een regio volgens een traject..
Het werd in 1828 in het werk gepubliceerd Wiskundige analyse van de theorieën van elektriciteit en magnetisme, geschreven door de Britse wiskundige George Green. Daarin worden vrij beslissende secties in de toepassing van calculus in de natuurkunde onderzocht, zoals het concept van potentiële functies, de functies van Green en de toepassingen van zijn titelloze stelling.
George Green formaliseerde zijn studentencarrière op 40-jarige leeftijd, tot nu toe een volledig autodidactische wiskundige. Na zijn studie aan de Universiteit van Cambridge, zette hij zijn onderzoek voort en leverde hij bijdragen op het gebied van akoestiek, optica en hydrodynamica die vandaag de dag nog steeds gelden..
De stelling van Green is een speciaal geval en komt voort uit 2 andere zeer belangrijke stellingen op het gebied van calculus. Dit zijn de stelling van Kelvin-Stokes en de divergentiestelling of Gauss Ostrogradski.
Uitgaande van een van de twee stellingen, is het mogelijk om tot de stelling van Green te komen. Bepaalde definities en proposities zijn nodig om dergelijke bewijzen te ontwikkelen..
- De volgende oefening laat zien hoe je een lijnintegraal transformeert in een dubbele integraal met betrekking tot een gebied R.
De oorspronkelijke uitdrukking is de volgende:
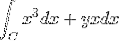
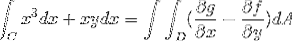
Van waar de functies die overeenkomen met f en g worden genomen
f (x, y) = x3 g (x, y) = yx
df / dy = 0 dg / dx = y
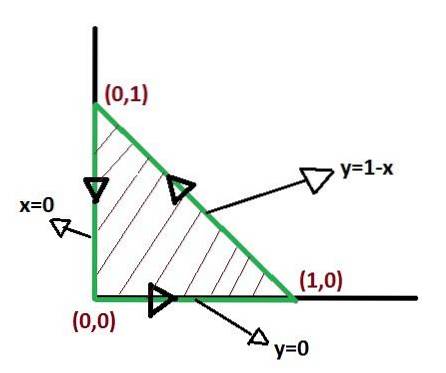
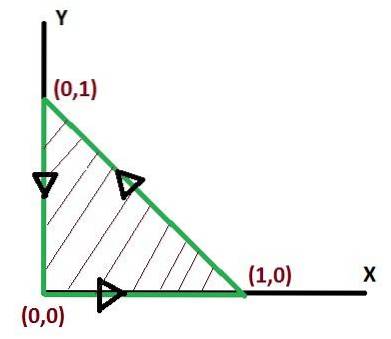
Er is geen enkele manier om de grenzen van integratie te definiëren bij het toepassen van de stelling van Green. Maar er zijn manieren waarop de integralen, nadat ze zijn gedefinieerd, eenvoudiger kunnen zijn. Het optimaliseren van de integratielimieten verdient dus aandacht.
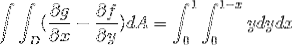
Waar krijgen we bij het oplossen van de integralen:
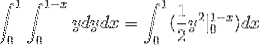
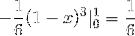
Deze waarde komt in kubieke eenheden overeen met het gebied onder de vectorfunctie en over het driehoekige gebied gedefinieerd door C.
Voor het geval van de lijnintegraal zonder de methode van Green uit te voeren, zou het nodig zijn geweest om de functies in elke sectie van de regio te parametriseren. Dat wil zeggen, voer 3 geparametriseerde integralen uit voor de resolutie. Dit is voldoende bewijs van de doeltreffendheid die Robert Green met zijn stelling bracht voor calculus.
Niemand heeft nog op dit artikel gereageerd.