
Superpositiestelling uitleg, toepassingen, opgeloste oefeningen
De superpositie stelling, In elektrische circuits stelt het vast dat de spanning tussen twee punten, of de stroom erdoorheen, de algebraïsche som is van de spanningen (of stromen als dit het geval is), als gevolg van elke bron, alsof elk op een andere manier handelde. Onafhankelijk.
Met deze stelling kunnen we lineaire circuits analyseren die meer dan één onafhankelijke bron bevatten, aangezien het alleen nodig is om de bijdrage van elk afzonderlijk te berekenen..

Lineaire afhankelijkheid is doorslaggevend voor de toepassing van de stelling. Een lineair circuit is een circuit waarvan de respons recht evenredig is met de invoer.
De wet van Ohm die op een elektrische weerstand wordt toegepast, stelt dat bijvoorbeeld V = i.R, waar V. is de spanning, R is de weerstand e ik is de stroom. Het is dan een lineaire afhankelijkheid van spanning en stroom in een weerstand.
In lineaire schakelingen wordt het superpositieprincipe toegepast waarbij rekening wordt gehouden met het volgende:
-Elke onafhankelijke spanningsbron moet afzonderlijk worden beschouwd en hiervoor is het noodzakelijk om alle andere uit te schakelen. Het volstaat om al degenen die niet worden geanalyseerd op 0 V te zetten of om ze in het schema te vervangen door een kortsluiting.
-Als de bron stroom is, moet je het circuit openen.
-Bij het beschouwen van de interne weerstand van zowel stroom- als spanningsbronnen, moeten ze op hun plaats blijven en deel uitmaken van de rest van het circuit..
-Als er afhankelijke bronnen zijn, moeten deze blijven zoals ze in het circuit voorkomen.
Artikel index
- 1 Toepassingen
- 2 Stappen om de superpositiestelling toe te passen
- 3 Opgeloste oefeningen
- 3.1 - Voorbeeld 1
- 3.2 - Oefening 2
- 4 referenties
Toepassingen
De superpositiestelling wordt gebruikt om eenvoudigere en gemakkelijker te hanteren circuits te verkrijgen. Maar er moet altijd rekening mee worden gehouden dat het alleen van toepassing is op mensen met lineaire reacties, zoals in het begin werd gezegd.
Het kan dus niet rechtstreeks worden gebruikt om bijvoorbeeld vermogen te berekenen, omdat vermogen gerelateerd is aan stroom door:
P = iktwee R
Omdat de stroom in het kwadraat is, is de respons niet lineair. Het is ook niet van toepassing op magnetische circuits met transformatoren..
Aan de andere kant biedt de superpositiestelling de mogelijkheid om het effect te kennen dat elke bron op het circuit heeft. En natuurlijk is het door de toepassing ervan mogelijk om het volledig op te lossen, dat wil zeggen om stromen en spanningen door elke weerstand te kennen.
De superpositiestelling kan ook worden gebruikt in combinatie met andere circuitstellingen, bijvoorbeeld die van Thévenin, om complexere configuraties op te lossen..
In wisselstroomcircuits is de stelling ook nuttig. In dit geval werken we met impedanties in plaats van weerstanden, zolang de totale respons van elke frequentie onafhankelijk kan worden berekend..
Ten slotte is in elektronische systemen de stelling van toepassing op zowel gelijkstroom- als wisselstroomanalyse, afzonderlijk.
Stappen om de superpositiestelling toe te passen
-Deactiveer alle onafhankelijke bronnen volgens de instructies die aan het begin zijn gegeven, behalve degene die moet worden geanalyseerd.
-Bepaal de output, hetzij spanning of stroom, die die enkele bron produceert.
-Herhaal de twee beschreven stappen voor alle andere bronnen.
-Bereken de algebraïsche som van alle bijdragen die in de vorige stappen zijn gevonden.
Opgeloste oefeningen
De uitgewerkte voorbeelden hieronder verduidelijken het gebruik van de stelling in enkele eenvoudige schakelingen.
- voorbeeld 1
Zoek in het circuit dat in de volgende afbeelding wordt getoond, de stroom door elke weerstand met behulp van de superpositiestelling.
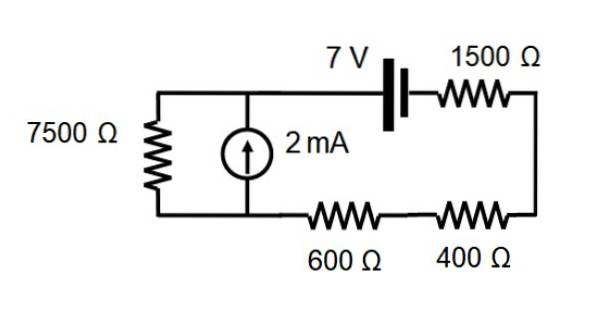
Oplossing
Bijdrage spanningsbron
Om te beginnen wordt de huidige bron geëlimineerd, waardoor het circuit er als volgt uitziet:

De equivalente weerstand wordt gevonden door de waarde van elke weerstand toe te voegen, aangezien ze allemaal in serie staan:
7500 +600 +400 + 1500 Ω = 10.000 Ω
De wet van Ohm toepassen V = I.R en het wissen van de stroom:
I = V / R = 7 / 10.000 A = 0.0007 A = 0,7 mA
Deze stroom is voor alle weerstanden gelijk.
Bijdrage van de huidige bron
De spanningsbron wordt onmiddellijk geëlimineerd om alleen met de huidige bron te werken. Het resulterende circuit wordt hieronder getoond:
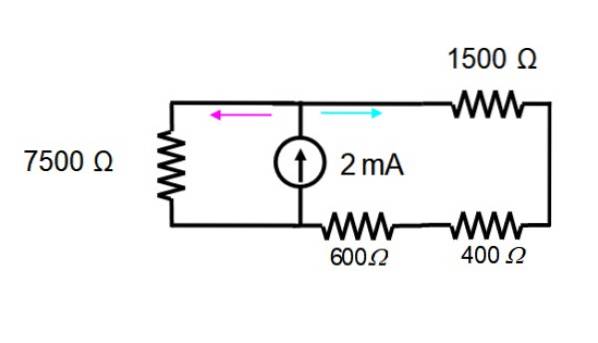
De weerstanden in het scherm rechts staan in serie en kunnen worden vervangen door een enkele:
600 +400 + 1500 Ω = 2500 Ω
Het resulterende circuit ziet er als volgt uit:
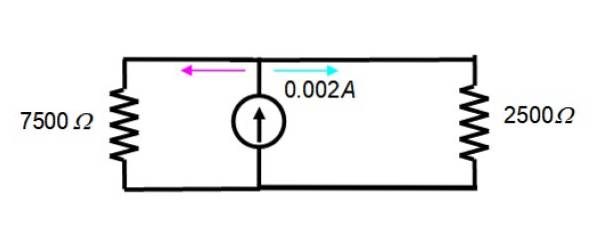
De stroom van 2 mA = 0,002 A is verdeeld over de twee weerstanden in de figuur, daarom is de vergelijking van de stroomverdeler geldig:
ikX = (Req/ RX) IkT
Waar ikX is de stroom in de weerstand RX, Req symboliseert de equivalente weerstand e ikT is de totale stroom. Het is noodzakelijk om de equivalente weerstand tussen beide te vinden, wetende dat:
1 / R.eq = (1 / R1) + (1 / Rtwee
Daarom:
1 / R.eq = (1/7500) + (1/2500) = 1/1875 → Req = 1875 Ω
Voor dit andere circuit wordt de stroom door de 7500 Ω-weerstand gevonden door waarden in de stroomverdelingsvergelijking te vervangen:
ik7500 Ω = (1875/7500). 0,002 A = 0,0005 A = 0,5 mA
Terwijl degene die door de 2500 Ω-weerstand gaat, is:
ik2500 Ω = 2 mA - 0,5 mA = 1,5 mA
Toepassing van de superpositiestelling
Nu wordt de superpositiestelling toegepast voor elke weerstand, te beginnen met de 400 Ω:
ik400 Ω = 1,5 mA - 0,7 mA = 0,8 mA
Belangrijk: voor deze weerstand, de stromen worden afgetrokken, terwijl ze in de tegenovergestelde richting circuleren, volgens een zorgvuldige observatie van de figuren, waarin de richtingen van de stromingen verschillende kleuren hebben.
Dezelfde stroom gaat evenredig door de weerstanden van 1500 Ω en 600 Ω, aangezien ze allemaal in serie zijn geschakeld.
De stelling wordt vervolgens toegepast om de stroom door de 7500 Ω-weerstand te vinden:
ik7500 Ω = 0,7 mA + 0,5 mA = 1,2 mA
Belangrijk: in het geval van de 7500 Ω-weerstand, houd er rekening mee dat de stromingen kloppen, omdat ze in beide circuits in dezelfde richting circuleren wanneer ze door deze weerstand gaan. Nogmaals, het is noodzakelijk om de richtingen van de stromingen zorgvuldig te observeren.
- Oefening 2
Het vinden van de stroom en spanning over de 12 Ω-weerstand met behulp van de superpositiestelling.
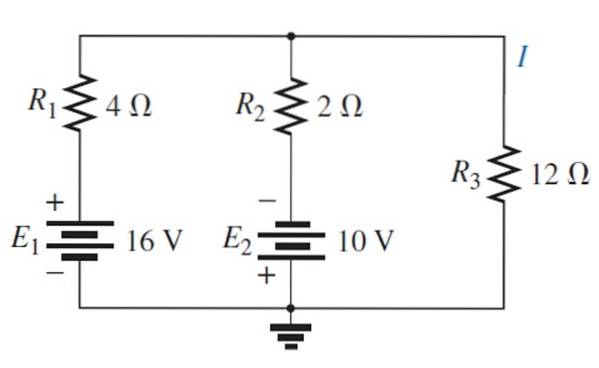
Oplossing
Lettertype E is vervangen1 met kortsluiting:
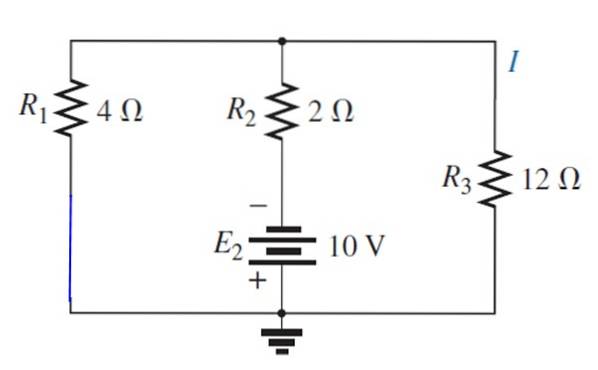
Het resulterende circuit is als volgt getekend om gemakkelijk de weerstanden te visualiseren die parallel blijven:
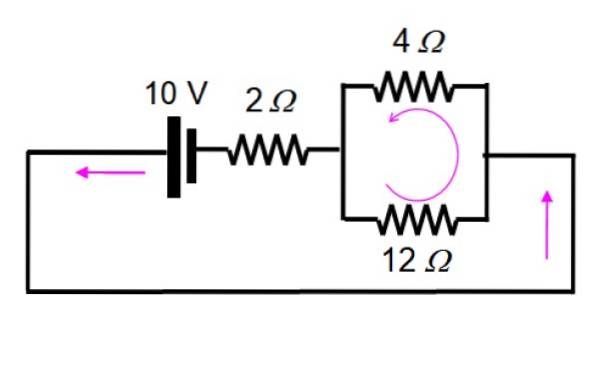
En nu is het opgelost door series en parallel toe te passen:
1 / R.eq = (1/12) + (1/4) = 1/3 → Req = 3 Ω
Deze weerstand is weer in serie met die van 2 Ω, daarom is de totale weerstand 5 Ω. De totale stroom is:
Ik = V / R = 10 V / 5 Ω = 2 EEN
Deze stream is onderverdeeld als:
ik12Ω = (3/12) 2 A = 0,5 A
Daarom is de spanning:
V.12Ω 0,5 A × 12 Ω = 6 V
Nu is bron E geactiveerd1
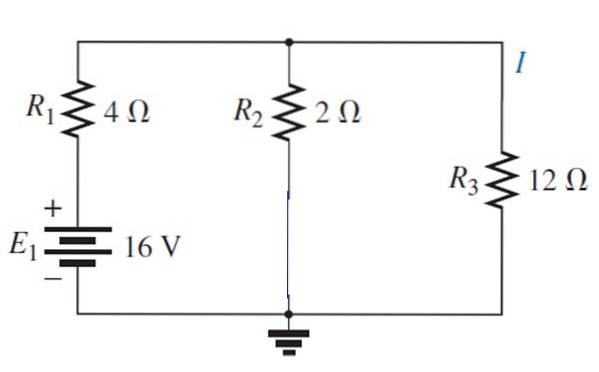
Het resulterende circuit kan als volgt worden getekend:

1 / R.eq = (1/12) + (1/2) = 7/12 → Req = 12/7 Ω
En in serie met die van 4 Ω een gelijkwaardige weerstand resulteert 40/7 Ω. In dit geval is de totale stroom:
Ik = V / R = 16 V / (40/7) Ω = 14/5 A
De spanningsdeler wordt opnieuw toegepast met deze waarden:
ik12Ω = ((12/7) / 12) (14/5) A = 0,4 EEN
De resulterende stroom is: 0,5 - 0,4 A = 0,1 A. Merk op dat ze zijn afgetrokken, omdat de stroom van elke bron een andere betekenis heeft, zoals te zien is in het originele circuit.
De spanning over de weerstand is:
V.12Ω 0,4 A × 12 Ω = 4,8 V
Ten slotte is de totale spanning: 6V-4.8V = 1.2V
Referenties
- Alexander, C. 2006. Grondbeginselen van elektrische schakelingen. 3e. Editie. Mc Graw Hill.
- Boylestad, R. 2011. Inleiding tot circuitanalyse. 2e. Editie. Pearson.
- Dorf, R. 2006. Inleiding tot elektrische schakelingen. 7e. Editie. John Wiley & Sons.
- Edminister, J. 1996. Electrical Circuits. Schaum-serie. 3e. Editie. Mc Graw Hill
- Wikipedia. Huidige verdeler. Hersteld van: es.wikipedia.org.


Niemand heeft nog op dit artikel gereageerd.