
De stelling van Varignon

Wat is de stelling van Varignon?
De stelling van Varignon, in Mechanics, stelt dat de som van de momenten geproduceerd door een systeem van gelijktijdige krachten met betrekking tot een bepaald punt gelijk is aan het moment van de resulterende kracht met betrekking tot hetzelfde punt.
Om deze reden wordt deze stelling ook wel het begin van momenten.
Hoewel de eerste die het uitsprak de Nederlander Simon Stevin (1548-1620) was, de maker van de hydrostatische paradox, was de Franse wiskundige Pierre Varignon (1654-1722) degene die het later zijn definitieve vorm gaf.
Een voorbeeld van hoe de stelling van Varignon werkt in Mechanics is het volgende: stel dat een eenvoudig systeem van twee coplanaire en gelijktijdige krachten inwerkt op een punt F.1 Y F.twee, (vetgedrukt vanwege hun vectorkarakter). Deze krachten geven aanleiding tot een netto of resulterende kracht, genaamd F.R.
Elke kracht oefent een koppel of moment uit rond een punt O, dat wordt berekend door het vectorproduct tussen de positievector rOP en de kracht F., waar rOP is gericht van O naar het punt van gelijktijdigheid P:
M.O1 rOP F.1
M.O2 rOP F.twee
Gezien de F.R F.1 + F.twee, dan:
M.OF rOP F.1 + rOP F.twee M.O1 + M.O2
Maar hoe rOP is een gemeenschappelijke factor, dan is het toepassen van distributieve eigenschap op het kruisproduct:
M.OF rOP (F.1 + F.twee rOP F.R
Daarom is de som van de momenten of koppels van elke kracht ten opzichte van punt O gelijk aan het moment van de resulterende kracht ten opzichte van hetzelfde punt..
Verklaring en bewijs
Laat een systeem zijn van N gelijktijdige krachten, gevormd door F.1, F.twee, F.3 F.N, waarvan de actielijnen elkaar kruisen bij punt P (zie figuur 1), het moment van dit krachtsysteem M.OF, met betrekking tot een punt O wordt gegeven door:
M.OF rOP F.1 + rOP F.twee + rOP F.3 + rOP F.N rOP (F.1 + F.twee + F.3 + F.N
Demonstratie
Om de stelling te bewijzen wordt gebruik gemaakt van de distributieve eigenschap van het vectorproduct tussen vectoren.
Wees de krachten F.1, F.twee, F.3 F.N toegepast op punten A1, NAARtwee, NAAR3… NAARN en gelijktijdig op punt P. Het resulterende moment van dit systeem, met betrekking tot een punt O, genoemd M.OF, is de som van de momenten van elke kracht, met betrekking tot genoemd punt:
M.OF = rOAi F.ik
Waar de som van i = 1 naar i = N gaat, aangezien er N krachten zijn. Omdat we te maken hebben met gelijktijdige krachten en aangezien het vectorproduct tussen parallelle vectoren nul is, gebeurt het dat:
rPAi F.ik 0
Met de nulvector aangeduid als 0.
Het moment van een van de krachten ten opzichte van O, bijvoorbeeld dat van de kracht F.ik toegepast in Aik, het is als volgt geschreven:
M.ik vernam rOAi F.ik
De positievector rOAi kan worden uitgedrukt als de som van twee positievectoren:
rOAi rOP + rPAi
Op deze manier komt het moment over O van de kracht F.ik het is:
M.ik vernam rOP + rPAi) F.ik rOP F.ikrPAi F.ik
Maar de laatste term is nul, zoals hierboven uitgelegd, omdat rPAi staat op het punt van actie F.ik, Dus:
M.ik vernam rOP F.ik
Wetende dat het moment van het systeem met betrekking tot punt O de som is van alle individuele momenten van elke kracht met betrekking tot dat punt, dan:
M.OF = M.ik vernam = rOP F.ik
Wat rOP is constant komt uit de som:
M.OF rOP F.ik
Maar ∑ F.ik is gewoon de netto kracht of resulterende kracht F.R, daarom wordt onmiddellijk geconcludeerd dat:
M.OF rOP F.R
Voorbeeld
De stelling van Varignon vergemakkelijkt de berekening van het krachtmoment F. Met betrekking tot punt O in de structuur getoond in de figuur, als de kracht wordt ontleed in zijn rechthoekige componenten en het moment van elk van hen wordt berekend:
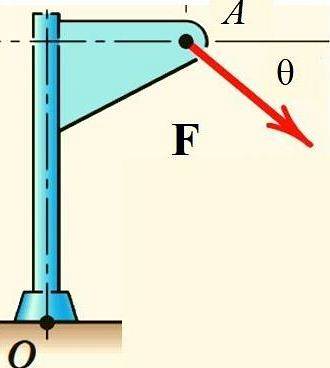
Toepassingen van de stelling van Varignon
Wanneer de resulterende kracht van een systeem bekend is, kan de stelling van Varignon worden toegepast om de som van elk van de momenten geproduceerd door de krachten waaruit het bestaat te vervangen door het moment van de resulterende.
Als het systeem bestaat uit krachten op hetzelfde vlak en het punt waarmee het moment moet worden berekend behoort tot dat vlak, dan is het resulterende moment loodrecht.
Als alle krachten zich bijvoorbeeld in het xy-vlak bevinden, is het moment gericht in de z-as en blijft het alleen om de grootte en de betekenis ervan te vinden, zoals het geval is in het hierboven beschreven voorbeeld.
In dit geval stelt de stelling van Varignon ons in staat om het resulterende moment van het systeem door de sommatie te berekenen. Het is erg handig in het geval van een driedimensionaal krachtsysteem, waarvan de richting van het resulterende moment niet a priori bekend is..
Om deze oefeningen op te lossen, is het handig om krachten te ontleden en vectoren te positioneren in hun rechthoekige componenten, en uit de som van de momenten de componenten van het nettomoment te bepalen.
Oefening opgelost
Bereken met behulp van de stelling van Varignon het moment van de kracht F rond het punt O dat in de afbeelding wordt weergegeven als de grootte van F 725 N is.
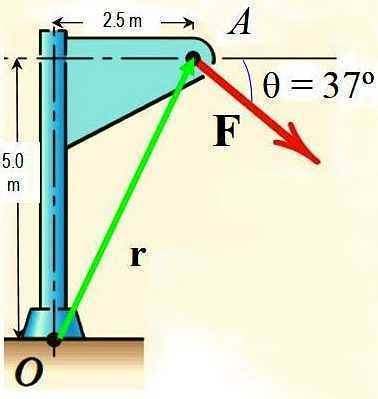
Oplossing
Om de stelling van Varignon toe te passen, ontleedt u de kracht F. in twee componenten, waarvan de respectievelijke momenten rond O worden berekend en opgeteld om het resulterende moment te verkrijgen.
F.X = 725 N ∙ cos 37 º = 579,0 N
F.Y = - 725 N N ∙ sin 37 º = −436,3 N
Evenzo de positievector r gericht van O naar A heeft de componenten:
rX = 2,5 m
rY = 5,0 m
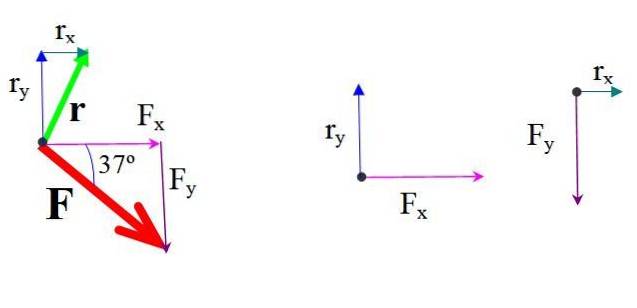
Het moment van elke component van de kracht rond O wordt gevonden door de kracht en de loodrechte afstand te vermenigvuldigen.
Beide krachten hebben de neiging om de structuur in dezelfde richting te draaien, wat in dit geval met de klok mee is, waaraan willekeurig een positief teken wordt toegewezen:
M.Os = FX∙ rY ∙ sin 90º = 579,0 N ∙ 5,0 m = 2895 N ∙ m
M.Oy = FY∙ rX ∙ sin (−90º) = −436,3 N ∙ 2,5 m ∙ (−1) = 1090,8 N ∙ m
Het resulterende moment over O is:
M.OF M.Os + M.Oy = 3985,8 N ∙ m loodrecht op het vlak en met de klok mee.
Referenties
- Bedford, 2000. A. Technische mechanica: statica. Addison Wesley.
- Beer, F. 2010. Statisch. McGraw Hill. 9e. Editie.
- Hibbeler, R. 1992. Mechanica voor ingenieurs. 6e. Editie. CECSA.
- HK Engineering. De stelling van Varignon. Hersteld van: youtube.com.
- Wikipedia. De stelling van Varignon (mechanica). Hersteld van: en.wikipedia.org.

Niemand heeft nog op dit artikel gereageerd.