
Karakteristieke vlakverdelingen, typen (regelmatig, onregelmatig), voorbeelden
De mozaïekpatroon zijn oppervlakken bedekt door een of meer figuren genoemd tegels. Ze zijn overal: in straten en allerlei soorten gebouwen. De tessera of tegels zijn platte stukken, meestal polygonen met congruente of isometrische kopieën, die volgens een regelmatig patroon worden geplaatst. Op deze manier blijven er geen ruimtes onbedekt en overlappen de tegels of mozaïeken elkaar niet..
In het geval dat een enkel type mozaïek wordt gebruikt dat wordt gevormd door een regelmatige veelhoek, is er een regelmatige mozaïekpatroon, maar als er twee of meer soorten regelmatige polygonen worden gebruikt, is het een semi-regelmatige mozaïekpatroon.

Ten slotte, als de polygonen die de mozaïekpatroon vormen niet regelmatig zijn, dan is het een onregelmatige mozaïekpatroon.
Het meest voorkomende type mozaïekpatroon wordt gevormd door rechthoekige en vooral vierkante mozaïeken. In figuur 1 hebben we een goed voorbeeld.
Artikel index
- 1 Geschiedenis van vlakvullingen
- 2 regelmatige vlakverdelingen
- 2.1 Nomenclatuur
- 2.2 Voorbeeld 1: driehoekige mozaïekpatroon
- 2.3 Voorbeeld 2: vierkante mozaïekpatroon
- 2.4 Voorbeeld 3: zeshoekige mozaïekpatroon
- 3 semi-regelmatige vlakverdelingen
- 3.1 Voorbeeld 4: Tri-hexagonale mozaïekpatroon
- 3.2 Voorbeeld 5: stompe zeshoekige mozaïekpatroon
- 3.3 Voorbeeld 6: rhombi-tri-hexagonale mozaïekpatroon
- 4 Onregelmatige vlakverdelingen
- 4.1 Voorbeeld 7
- 4.2 Voorbeeld 8
- 4.3 Voorbeeld 9
- 4.4 Voorbeeld 10: mozaïekpatroon in Caïro
- 4.5 Voorbeeld 11: Al-Andalus mozaïekpatroon
- 4.6 Voorbeeld 12: mozaïekpatroon in videogames
- 5 referenties
Geschiedenis van vlakvullingen
Al duizenden jaren wordt mozaïekpatroon gebruikt om vloeren en muren van paleizen en tempels van verschillende culturen en religies te bedekken..
Bijvoorbeeld de Soemerische beschaving die bloeide rond 3500 voor Christus. ten zuiden van Mesopotamië, tussen de Eufraat en de Tigris, gebruikten ze vlakvullingen in hun architectuur.

Tessellations hebben ook de interesse gewekt van wiskundigen van alle leeftijden: te beginnen met Archimedes in de 3e eeuw voor Christus, gevolgd door Johannes Kepler in 1619, Camille Jordan in 1880, tot de huidige tijd met Roger Penrose..
Penrose creëerde een niet-periodiek mozaïekpatroon dat bekend staat als Penrose mozaïekpatroon. ENdeze zijn slechts enkele namen van wetenschappers die veel hebben bijgedragen aan mozaïekpatroon.
Regelmatige vlakvullingen
Regelmatige vlakverdelingen worden gemaakt met slechts één type regelmatige veelhoek. Aan de andere kant, om de mozaïekpatroon als regelmatig te beschouwen, moet elk punt van het vlak:
-Behoren tot het interieur van veelhoek
-Of aan de rand van twee aangrenzende polygonen
-Ten slotte kan het behoren tot het gemeenschappelijke hoekpunt van ten minste drie polygonen.
Met de bovenstaande beperkingen kan worden aangetoond dat alleen gelijkzijdige driehoeken, vierkanten en zeshoeken een regelmatige mozaïekpatroon kunnen vormen.
Nomenclatuur
Er is een nomenclatuur om tessellations aan te duiden die bestaat uit een lijst met de klok mee en gescheiden door een punt, het aantal zijden van de polygonen die elk knooppunt (of hoekpunt) van de tessellatie omringen, altijd beginnend met de polygoon met het laagste nummer. zijkanten.
Deze nomenclatuur is van toepassing op regelmatige en semi-regelmatige vlakverdelingen.
Voorbeeld 1: driehoekige mozaïekpatroon
Figuur 3 toont een regelmatige driehoekige mozaïekpatroon. Opgemerkt moet worden dat elk knooppunt van de driehoekige mozaïekpatroon het gemeenschappelijke hoekpunt is van zes gelijkzijdige driehoeken.
De manier om dit type mozaïekpatroon aan te duiden is 3.3.3.3.3.3, dat ook wordt aangeduid met 36.

Voorbeeld 2: vierkante mozaïekpatroon
Figuur 4 toont een regelmatig mozaïekpatroon dat alleen uit vierkanten bestaat. Opgemerkt moet worden dat elk knooppunt in het mozaïekpatroon wordt omgeven door vier congruente vierkanten. De notatie die wordt toegepast op dit type vierkante mozaïekpatroon is: 4.4.4.4 of alternatief 44

Voorbeeld 3: zeshoekige mozaïekpatroon
In een hexagonaal mozaïekpatroon wordt elk knooppunt omgeven door drie regelmatige zeshoeken, zoals weergegeven in figuur 5. De nomenclatuur voor een regelmatig hexagonaal mozaïekpatroon is 6.6.6 of 63.

Semi-regelmatige vlakverdelingen
Semi-regelmatige of archimedische vlakverdelingen bestaan uit twee of meer soorten regelmatige polygonen. Elk knooppunt is omgeven door de soorten polygonen waaruit het mozaïekpatroon bestaat, altijd in dezelfde volgorde, en de randvoorwaarde wordt volledig gedeeld met de buurman..
Er zijn acht semi-regelmatige vlakverdelingen:
- 3.6.3.6 (tri-hexagonale mozaïekpatroon)
- 3.3.3.3.6 (stompe zeshoekige mozaïekpatroon)
- 3.3.3.4.4 (langwerpige driehoekige mozaïekpatroon)
- 3.3.4.3.4 (stomp vierkant mozaïekpatroon)
- 3.4.6.4 (rhombi-tri-hexagonale mozaïekpatroon)
- 4.8.8 (afgeknotte vierkante mozaïekpatroon)
- 3.12.12 (afgeknotte zeshoekige mozaïekpatroon)
- 4.6.12 (afgeknotte tri-hexagonale mozaïekpatroon)
Enkele voorbeelden van semi-regelmatige vlakverdelingen worden hieronder weergegeven.
Voorbeeld 4: Tri-hexagonale mozaïekpatroon
Het is degene die is samengesteld uit gelijkzijdige driehoeken en regelmatige zeshoeken in de 3.6.3.6-structuur, wat betekent dat een knooppunt van het mozaïekpatroon wordt omgeven (tot het voltooien van een draai) door een driehoek, een zeshoek, een driehoek en een zeshoek. Figuur 6 toont zo'n mozaïekpatroon.

Voorbeeld 5: stompe zeshoekige mozaïekpatroon
Net als de mozaïekpatroon in het vorige voorbeeld, bestaat deze ook uit driehoeken en zeshoeken, maar hun verdeling rond een knoop is 3.3.3.3.6. Figuur 7 illustreert duidelijk dit type mozaïekpatroon.

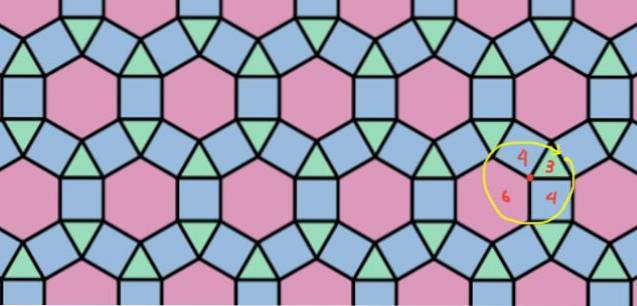
Voorbeeld 6: rhombi-tri-hexagonale mozaïekpatroon
Het is een mozaïekpatroon dat bestaat uit driehoeken, vierkanten en zeshoeken, in de configuratie 3.4.6.4, die wordt weergegeven in figuur 8.
Onregelmatige vlakverdelingen
Onregelmatige vlakverdelingen zijn die welke worden gevormd door onregelmatige veelhoeken of door regelmatige veelhoeken, maar die niet voldoen aan het criterium dat een knooppunt een hoekpunt is van ten minste drie veelhoeken.
Voorbeeld 7
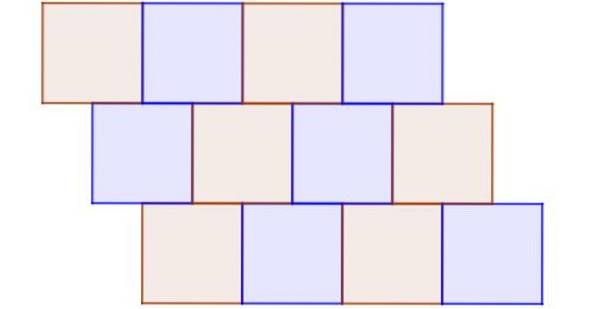
Figuur 9 toont een voorbeeld van een onregelmatige mozaïekpatroon, waarin alle polygonen regelmatig en congruent zijn. Het is onregelmatig omdat een knoop geen gemeenschappelijk hoekpunt is van ten minste drie vierkanten en er ook aangrenzende vierkanten zijn die een rand niet volledig delen.
Voorbeeld 8
Het parallellogram betegelt een plat oppervlak, maar tenzij het een vierkant is, kan het geen regelmatig mozaïekpatroon vormen.

Voorbeeld 9
Niet-regelmatige zeshoeken met centrale symmetrie tessellate een plat oppervlak, zoals weergegeven in de volgende afbeelding:

Voorbeeld 10: mozaïekpatroon in Caïro
Het is een zeer interessante mozaïekpatroon, samengesteld uit vijfhoeken met zijden van gelijke lengte maar met ongelijke hoeken, waarvan er twee recht zijn en de andere drie elk 120 ° hebben..
De naam komt van het feit dat deze mozaïekpatroon wordt gevonden in de bestrating van enkele straten van Caïro in Egypte. Figuur 12 toont de mozaïekpatroon van Caïro.

Voorbeeld 11: Al-Andalus-mozaïekpatroon
De mozaïekpatroon in sommige delen van Andalusië en Noord-Afrika wordt gekenmerkt door geometrie en epigrafie, naast decoratieve elementen zoals vegetatie..
Het mozaïekpatroon van paleizen zoals dat van het Alhambra bestond uit tegels die waren gemaakt van keramische stukken in vele kleuren, met meerdere (zo niet oneindige) vormen die geometrische patronen ontketenden..

Voorbeeld 12: mozaïekpatroon in videogames
Ook bekend als tesellatie, is het een van de meest populaire nieuwigheden in videogames. Het gaat om het creëren van texturen om de mozaïekpatroon van de verschillende scenario's die in de simulator verschijnen te simuleren.
Dit is de duidelijke weerspiegeling dat deze coatings blijven evolueren en de grenzen van de werkelijkheid overschrijden..
Referenties
- Geniet van wiskunde. Tessellations. Hersteld van: gustolasmatematicas.com
- Rubiños. Tessellations loste voorbeelden op. Hersteld van: matematicasn.blogspot.com
- Weisstein, Eric W. "Demiregular mozaïekpatroon". Weisstein, Eric W, ed. MathWorld. Wolfram Research.
- Wikipedia. Mozaïekpatroon. Hersteld van: es.wikipedia.com
- Wikipedia. Regelmatige mozaïekpatroon. Hersteld van: es.wikipedia.com



Niemand heeft nog op dit artikel gereageerd.