
Verticale shotformules, vergelijkingen, voorbeelden
De verticaal schot Het is een beweging die plaatsvindt onder invloed van een krachtveld, gewoonlijk dat van de zwaartekracht, en kan stijgen of dalen. Het is ook bekend onder de naam verticale lancering.
Het meest directe voorbeeld is het overgeven (of naar beneden als je dat liever hebt) een bal met je hand, natuurlijk, en zorg ervoor dat je dit in verticale richting doet. De luchtweerstand buiten beschouwing gelaten, past de beweging die de bal volgt perfect in het Uniformly Varied Rectilinear Motion (MRUV) -model..

De verticale opname is een beweging die veel wordt bestudeerd in inleidende natuurkundecursussen, omdat het een voorbeeld is van de beweging in één dimensie, een heel eenvoudig en handig model.
Dit model kan niet alleen worden gebruikt om de kinematica van objecten onder invloed van de zwaartekracht te bestuderen, maar beschrijft ook, zoals later zal worden gezien, de beweging van deeltjes in het midden van een uniform elektrisch veld..
Artikel index
- 1 Formules en vergelijkingen
- 1.1 Verticale worpvergelijkingen
- 2 voorbeelden
- 2.1 Uitgewerkt voorbeeld 1
- 2.2 Uitgewerkt voorbeeld 2
- 3 referenties
Formules en vergelijkingen
Het eerste dat nodig is, is een coördinatensysteem om de oorsprong aan te duiden en deze te labelen met een letter, wat in het geval van verticale bewegingen de letter is "Y.
Vervolgens wordt de positieve richting geselecteerd +Y, dat is meestal naar boven en het gevoel -Y die meestal wordt verwijderd (zie figuur 2). Dit alles tenzij de probleemoplosser anders beslist, aangezien een andere optie is om de richting van de beweging als positief te beschouwen, wat het ook mag zijn..
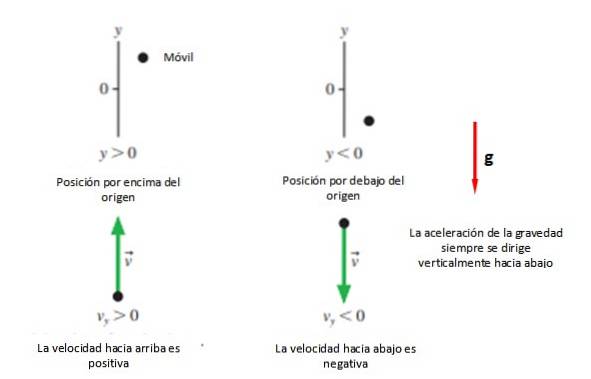
In ieder geval wordt aanbevolen dat de oorsprong samenvalt met het startpunt. Yof, omdat op deze manier de vergelijkingen worden vereenvoudigd, hoewel je elke gewenste positie kunt innemen om de beweging te bestuderen.
Verticale worpvergelijkingen
Zodra we het coördinatensysteem en de oorsprong hebben vastgesteld, gaan we naar de vergelijkingen. De grootheden die de beweging beschrijven zijn:
-Initiële snelheid vof
-Versnelling naar
-Snelheid v
-Startpositie Xof
-Positie X
-Verplaatsing DX
-Weer t
Behalve de tijd zijn alle vectoren vectoren, maar aangezien het een eendimensionale beweging is met een bepaalde richting, is het van belang om + of - tekens te gebruiken om aan te geven waar de betreffende magnitude naartoe gaat. Bij verticale diepgang gaat de zwaartekracht altijd naar beneden en wordt, tenzij anders aangegeven, een teken toegekend -.
Hieronder volgen de vergelijkingen die zijn aangepast voor verticale diepgang, in de plaats van "X" voor "Y"Y"naar" voor "gBovendien wordt het teken (-) dat overeenkomt met de naar beneden gerichte zwaartekracht onmiddellijk toegevoegd:
1) Positie y = yof + vof.t - ½ g.ttwee
2) Snelheid v = vof - g.t
3) Snelheid als functie van verplaatsing ΔY vtwee = voftwee - 2 g. ΔY
Voorbeelden
Hieronder staan toepassingsvoorbeelden voor verticaal fotograferen. In zijn resolutie moet met het volgende rekening worden gehouden:
-g”Heeft een constante waarde die gemiddeld 9,8 m / s istwee of ongeveer 10 m / stwee indien gewenst om berekeningen te vergemakkelijken wanneer te veel precisie niet vereist is.
-Wanneer vof Oke 0, deze vergelijkingen reduceren tot die van vrije val.
-Als de lancering naar boven is gericht, moet het object een beginsnelheid hebben waarmee het kan bewegen. Eenmaal in beweging bereikt het object een maximale hoogte die afhangt van hoe groot de beginsnelheid is. Hoe hoger de hoogte, hoe meer tijd de mobiel in de lucht zal doorbrengen.
-Het object keert terug naar het startpunt met dezelfde snelheid waarmee het werd gegooid, maar de snelheid is naar beneden gericht.
-Voor een neerwaartse verticale lancering geldt: hoe hoger de beginsnelheid, hoe eerder het object de grond zal raken. Hier wordt de afgelegde afstand ingesteld volgens de geselecteerde hoogte voor de lancering.
-Bij de verticale opwaartse worp wordt de tijd die de mobiel nodig heeft om de maximale hoogte te bereiken, berekend door te doen v = 0 in vergelijking 2) van de vorige sectie. Dit is de maximale tijd tmax. hoogte
0 = vof - g. tmax. hoogte tmax. hoogte = vof / g
-De maximale hoogte Ymax. hoogte wordt gewist uit vergelijking 3) van de vorige sectie door op dezelfde manier te doen v = 0
0 = voftwee - 2 g. Δy ⇒ 0 = voftwee - 2 g. (Ymax. hoogte - Yof) ⇒ enmax. hoogte = enof + voftwee / 2 g
Ja Yof = 0, Het wordt teruggebracht tot:
Ymax. hoogte = voftwee / 2 g
Uitgewerkt voorbeeld 1
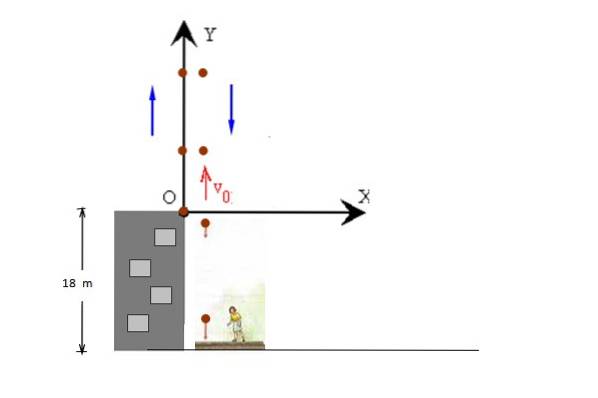
Een bal wordt verticaal naar boven geworpen met vof = 14 m / s, vanaf de top van een 18 m hoog gebouw. De bal mag zijn weg vervolgen naar het trottoir. Berekenen:
a) De maximale hoogte die de bal bereikt ten opzichte van de grond.
b) De tijd dat het in de lucht was (vluchttijd.
Oplossing
De figuur toont voor de duidelijkheid de op- en neergaande bewegingen van de bal afzonderlijk, maar beide vinden langs dezelfde lijn plaats. De beginpositie wordt ingenomen op y = 0, zodat de eindpositie y = - 18 m is.
a) De maximale hoogte gemeten vanaf het dak van het gebouw is Ymax. hoogte = voftwee / 2 g en uit de verklaring kunnen we lezen dat de beginsnelheid +14 m / s is, dan:
Ymax. hoogte = (14 m / s)twee / 2 x 9,8 m / stwee = 10 m (Met betrekking tot het dak)
H.max. hoogte = 10 m + 18 m = 28 m (Betreffende het trottoir).
b) Om het totale tijd of vluchttijd de bal blijft in de lucht, wordt de vergelijking gebruikt y = yof + vof.t - ½ g.ttwee, met de volgende waarden en tekens:
y = - 18 m
Yof = 0 m
vof = +14 m / s
Vervanging:
- 18 = 14.t - ½ 9,8 .ttwee
- 4,9 tontwee+14. t + 18 = 0
4,9 tontwee-14. t - 18 = 0
Het is een vergelijking van de tweede graad die gemakkelijk kan worden opgelost met behulp van een wetenschappelijke rekenmachine of met behulp van de oplosser. De oplossingen zijn: 3.82 en -0.96. De negatieve oplossing wordt weggegooid omdat het, aangezien het een tijd is, geen fysiek gevoel heeft.
De vliegtijd van de bal is 3,82 seconden.
Uitgewerkt voorbeeld 2
Een positief geladen deeltje met q = +1,2 millicoulomb (mC) en massa m = 2,3 x 10 -10 Kg wordt verticaal naar boven geprojecteerd, beginnend vanaf de in de figuur weergegeven positie en met beginsnelheid vof = 30 km / s.
Tussen de opgeladen platen bevindt zich een elektrisch veld EN uniform, verticaal naar beneden gericht en met een magnitude van 780 N / C. Als de afstand tussen de platen 18 cm is, komt het deeltje dan in botsing met de bovenplaat? Verwaarloos de aantrekkingskracht op het deeltje, aangezien het extreem licht is.
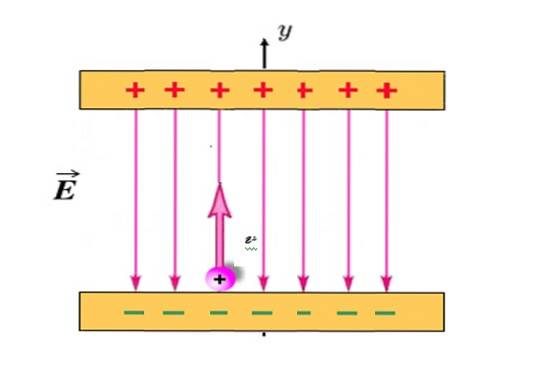
Oplossing
Bij dit probleem het elektrische veld EN is degene die een kracht produceert F. en de daaruit voortvloeiende versnelling. Positief geladen, wordt het deeltje altijd aangetrokken door de onderste plaat, maar wanneer het verticaal naar boven wordt geprojecteerd, zal het een maximale hoogte bereiken en dan terugkeren naar de onderste plaat, net als de bal in de vorige voorbeelden..
Per definitie van elektrisch veld:
E = F / q = m.a / q ⇒ a = q.E / m
U moet deze equivalentie gebruiken voordat u waarden vervangt:
1 mC = 1 x 10-3 C
De versnelling is dus:
a = 1,2 x 10-3 x 780 / 2,3 x 10 -10Mevrouwtwee = 4,07 x 109 Mevrouwtwee
Voor de maximale hoogte wordt de formule uit de vorige sectie gebruikt, maar in plaats van 'g"Deze versnellingswaarde wordt gebruikt:
Ymax. hoogte = voftwee / 2a = (30.000 m / s)twee/ 2 x 4,07 x 109 Mevrouwtwee = 0,11 m = 11 cm
Het botst niet met de bovenplaat, aangezien het 18 cm van het startpunt is en het deeltje slechts 11 cm reikt.
Referenties
- Kirkpatrick, L. 2007. Natuurkunde: een blik op de wereld. 6ta Verkorte editie. Cengage leren. 23 - 27.
- Rex, A. 2011. Fundamentals of Physics. Pearson. 33 - 36
- Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14th. Ed. Deel 1. 50 - 53.
- Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9na Ed. Cengage Learning. 43 - 55.
- Wilson, J. 2011. Physics 10. Pearson Education. 133 - 149.


Niemand heeft nog op dit artikel gereageerd.