
Eigenschappen gelijkbenige driehoek, formule en oppervlakte, berekening

EEN gelijkbenige driehoek is een veelhoek met drie zijden, waarvan er twee dezelfde maat hebben en de derde zijde een andere maat. Deze laatste zijde wordt de basis genoemd. Vanwege dit kenmerk kreeg het deze naam, wat in het Grieks "gelijke benen" betekent
Driehoeken zijn polygonen die als de eenvoudigste in geometrie worden beschouwd, omdat ze bestaan uit drie zijden, drie hoeken en drie hoekpunten. Zij zijn degenen die het minste aantal zijden en hoeken hebben ten opzichte van de andere polygonen, maar hun gebruik is zeer uitgebreid.

Artikel index
- 1 Kenmerken van gelijkbenige driehoeken
- 1.1 Componenten
- 2 Eigenschappen
- 2.1 Interne hoeken
- 2.2 Som van de zijkanten
- 2.3 Congruente kanten
- 2.4 Congruente hoeken
- 2.5 Hoogte, mediaan, bissectrice en middelloodlijn vallen samen
- 2.6 Relatieve hoogtes
- 2.7 Coincident orthocenter, barycenter, incenter en circumcenter
- 3 Hoe de omtrek te berekenen?
- 4 Hoe de hoogte te berekenen?
- 5 Hoe de oppervlakte te berekenen?
- 6 Hoe de basis van de driehoek te berekenen?
- 7 oefeningen
- 7.1 Eerste oefening
- 7.2 Tweede oefening
- 7.3 Derde oefening
- 8 referenties
Kenmerken van gelijkbenige driehoeken
De gelijkbenige driehoek werd geclassificeerd met de maat van de zijkanten als een parameter, aangezien twee van de zijkanten congruent zijn (ze hebben dezelfde lengte).
Op basis van de amplitude van de binnenhoeken worden gelijkbenige driehoeken geclassificeerd als:
- Gelijkbenige rechthoekige driehoek: twee van de zijden zijn gelijk. Een van de hoeken is goed (90of) en de anderen zijn hetzelfde (45of elk)
- Gelijkbenige stompe driehoek: twee van de zijden zijn gelijk. Een van de hoeken is stomp (> 90of.
- Gelijkbenige acute driehoek: twee van de zijden zijn gelijk. Al zijn hoeken zijn acuut (< 90of), waarbij twee dezelfde maat hebben.
Componenten
- Mediaan: is een lijn die begint vanaf het middelpunt van de ene kant en het andere hoekpunt bereikt. De drie medianen komen samen op een punt dat het zwaartepunt of zwaartepunt wordt genoemd..
- Bissectrice: is een straal die de hoek van elk hoekpunt verdeelt in twee hoeken van gelijke grootte. Daarom staat het bekend als de symmetrieas en heeft dit type driehoeken er maar één.
- De middelste: is een segment loodrecht op de zijkant van de driehoek, dat zijn oorsprong heeft in het midden van de driehoek. Er zijn drie bemiddelaars in een driehoek en ze ontmoeten elkaar op een punt dat circumcenter wordt genoemd.
- De hoogte: is de lijn die van het hoekpunt naar de tegenoverliggende zijde gaat en ook deze lijn staat loodrecht op die zijde. Alle driehoeken hebben drie hoogtes, die samenvallen op een punt dat het orthocentrum wordt genoemd..
Eigendommen
Gelijkbenige driehoeken worden gedefinieerd of geïdentificeerd omdat ze verschillende eigenschappen hebben die hen vertegenwoordigen, afkomstig van de stellingen die zijn voorgesteld door grote wiskundigen:
Interne hoeken
De som van de binnenhoeken is altijd gelijk aan 180of.
Som van de zijkanten
De som van de maten van twee zijden moet altijd groter zijn dan de maat van de derde zijde, a + b> c.
Congruente kanten
Gelijkbenige driehoeken hebben twee zijden met dezelfde maat of lengte; dat wil zeggen, ze zijn congruent en de derde kant is anders dan deze.
Congruente hoeken
Gelijkbenige driehoeken staan ook bekend als iso-hoekige driehoeken, omdat ze twee hoeken hebben die dezelfde maat hebben (congruent). Deze bevinden zich aan de basis van de driehoek, tegenover de zijden met dezelfde lengte.
Hierdoor werd de stelling gegenereerd die stelt dat:
"Als een driehoek twee congruente zijden heeft, zullen de hoeken tegenover die zijden ook congruent zijn." Daarom, als een driehoek gelijkbenig is, zijn de hoeken van de bases congruent.
Voorbeeld:
De volgende afbeelding toont een driehoek ABC. Door de middelloodlijn van het hoekpunt van hoek B naar de basis te trekken, wordt de driehoek verdeeld in twee gelijke driehoeken BDA en BDC:
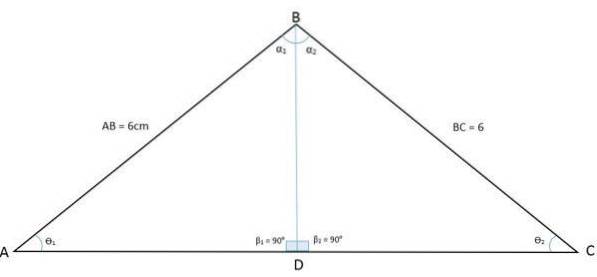
Op deze manier werd de hoek van top B ook verdeeld in twee gelijke hoeken. De middelloodlijn is nu de gemeenschappelijke zijde (BD) tussen die twee nieuwe driehoeken, terwijl de zijden AB en BC de congruente zijden zijn. We hebben dus het geval van congruentie zijde, hoek, zijde (LAL).
Dit toont aan dat de hoeken van de hoekpunten A en C dezelfde maat hebben, en er kan ook worden aangetoond dat aangezien de driehoeken BDA en BDC congruent zijn, de zijden AD en DC ook congruent zijn..
Hoogte, mediaan, bissectrice en middelloodlijn vallen samen
De lijn die wordt getrokken vanaf het hoekpunt tegenover de basis naar het middelpunt van de basis van de gelijkbenige driehoek, is tegelijkertijd de hoogte, de mediaan en de middelloodlijn, evenals de middelloodlijn ten opzichte van de tegenoverliggende hoek van de basis..
Al deze segmenten vallen samen in één die hen vertegenwoordigt.
Voorbeeld:
De volgende afbeelding toont de driehoek ABC met een middelpunt M die de basis in twee segmenten BM en CM verdeelt.
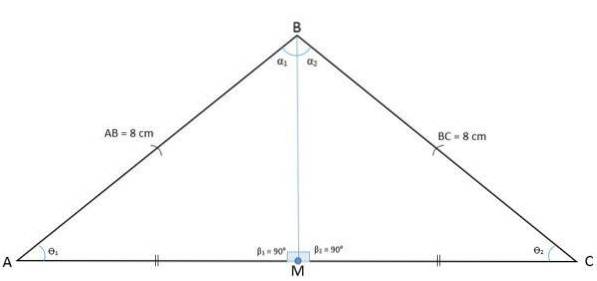
Door een segment van punt M naar het tegenoverliggende hoekpunt te trekken, wordt per definitie de mediaan AM verkregen, die relatief is ten opzichte van hoekpunt A en zijde BC.
Aangezien het segment AM de driehoek ABC in twee gelijke driehoeken AMB en AMC verdeelt, betekent dit dat het geval van congruentie zijde, hoek en zijde zal zijn en daarom zal AM ook de middelloodlijn zijn van BÂC.
Daarom is de middelloodlijn altijd gelijk aan de mediaan en vice versa..
Het segment AM vormt hoeken die dezelfde maat hebben voor de driehoeken AMB en AMC; dat wil zeggen, ze zijn zodanig aanvullend dat de maat van elk zal zijn:
Med. (AMB) + Med. (AMC) = 180of
twee Med. (AMC) = 180of
Med. (AMC) = 180of ÷ 2
Med. (AMC) = 90of
Het is bekend dat de hoeken gevormd door segment AM ten opzichte van de basis van de driehoek juist zijn, wat aangeeft dat dit segment geheel loodrecht op de basis staat..
Geeft daarom de hoogte en de middelloodlijn weer, wetende dat M het middelpunt is.
Daarom is de regel AM:
- Vertegenwoordigt op het hoogtepunt van BC.
- Is middelgroot.
- Het is opgenomen in de middelloodlijn van BC.
- Het is de middelloodlijn van de tophoek Â
Relatieve hoogtes
Hoogtes die relatief zijn ten opzichte van gelijke zijden hebben ook dezelfde afmeting.
Omdat de gelijkbenige driehoek twee gelijke zijden heeft, zullen hun twee respectieve hoogtes ook gelijk zijn..
Ortocentrum, zwaartepunt, incenter en samenvallende circumcenter
Aangezien de hoogte, mediaan, middelloodlijn en middelloodlijn ten opzichte van de basis tegelijkertijd worden weergegeven door hetzelfde segment, zullen het orthocentrum, middelste zwaartepunt en circumcenter collineaire punten zijn, dat wil zeggen, ze zullen op dezelfde lijn liggen:

Hoe de omtrek te berekenen?
De omtrek van een veelhoek wordt berekend door de zijkanten op te tellen.
Omdat in dit geval de gelijkbenige driehoek twee zijden heeft met dezelfde maat, wordt de omtrek berekend met de volgende formule:
P = 2(zijde a) + (zijde b).
Hoe de hoogte te berekenen?
De hoogte is de lijn loodrecht op de basis, het verdeelt de driehoek in twee gelijke delen terwijl het zich uitstrekt naar het tegenoverliggende hoekpunt.
De hoogte vertegenwoordigt het tegenoverliggende been (a), het midden van de basis (b / 2) het aangrenzende been en de zijde "a" vertegenwoordigt de hypotenusa.
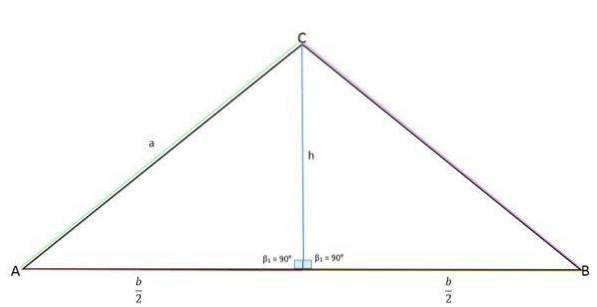
Met behulp van de stelling van Pythagoras kan de waarde van de hoogte worden bepaald:
naartwee + btwee ctwee
Waar:
naartwee = hoogte (h).
btwee = b / 2.
ctwee = kant a.
Als we deze waarden in de stelling van Pythagoras vervangen en de hoogte oplossen, hebben we:
htwee + b / twee)twee naartwee
htwee + btwee / 4 = naartwee
htwee naartwee - btwee / 4
h = √ (naartwee - btwee / 4).
Als de hoek gevormd door de congruente zijden bekend is, kan de hoogte worden berekend met de volgende formule:

Hoe de oppervlakte te berekenen?
De oppervlakte van de driehoeken wordt altijd berekend met dezelfde formule, waarbij de basis vermenigvuldigd wordt met de hoogte en gedeeld door twee:

Er zijn gevallen waarin alleen de afmetingen van twee zijden van de driehoek en de hoek die ertussen wordt gevormd bekend zijn. In dit geval is het om het gebied te bepalen nodig om de trigonometrische verhoudingen toe te passen:
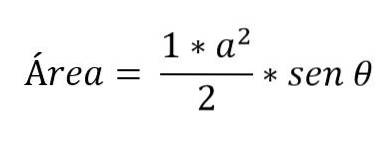
Hoe de basis van de driehoek te berekenen?
Omdat de gelijkbenige driehoek twee gelijke zijden heeft, is het voor het bepalen van de waarde van de basis noodzakelijk om ten minste de hoogte of een van de hoeken te kennen..
Als we de hoogte kennen, wordt de stelling van Pythagoras gebruikt:
naartwee + btwee = ctwee
Waar:
naartwee = hoogte (h).
ctwee = kant a.
btwee = b / 2, is onbekend.
We lossen op voor btwee van de formule en we moeten:
btwee = eentwee - ctwee
b = √ eentwee - ctwee
Aangezien deze waarde overeenkomt met de helft van de basis, moet deze met twee worden vermenigvuldigd om de volledige maat van de basis van de gelijkbenige driehoek te verkrijgen:
b = 2 (√ eentwee - ctwee
In het geval dat alleen de waarde van de gelijke zijden en de hoek ertussen bekend zijn, wordt trigonometrie toegepast, waarbij een lijn wordt getrokken van het hoekpunt naar de basis die de gelijkbenige driehoek in twee rechthoekige driehoeken verdeelt.
Op deze manier wordt de helft van de basis berekend met:

Het is ook mogelijk dat alleen de waarde van de hoogte en hoek van de top die tegenover de basis ligt bekend is. In dat geval kan door trigonometrie de basis worden bepaald:

Opleiding
Eerste oefening
Zoek het gebied van de gelijkbenige driehoek ABC, wetende dat twee zijden 10 cm zijn en de derde zijde 12 cm.
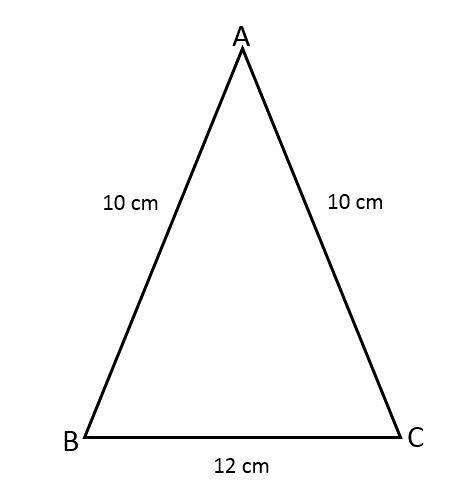
Oplossing
Om de oppervlakte van de driehoek te vinden, is het noodzakelijk om de hoogte te berekenen met behulp van de oppervlakte-formule die gerelateerd is aan de stelling van Pythagoras, aangezien de waarde van de hoek gevormd tussen de gelijke zijden niet bekend is.
We hebben de volgende gegevens van de gelijkbenige driehoek:
- Gelijke zijden (a) = 10 cm.
- Basis (b) = 12 cm.
De waarden worden in de formule vervangen:

Tweede oefening
De lengte van de twee gelijke zijden van een gelijkbenige driehoek is 42 cm, de vereniging van deze zijden vormt een hoek van 130of. Bepaal de waarde van de derde zijde, de oppervlakte van die driehoek en de omtrek.
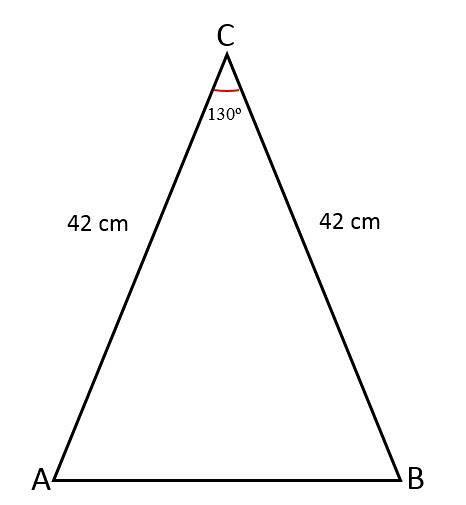
Oplossing
In dit geval zijn de afmetingen van de zijkanten en de hoek ertussen bekend..
Om de waarde van de ontbrekende zijde te weten, dat wil zeggen, de basis van die driehoek, wordt een lijn loodrecht erop getekend, die de hoek in twee gelijke delen verdeelt, één voor elke rechthoekige driehoek die wordt gevormd.
- Gelijke zijden (a) = 42 cm.
- Hoek (Ɵ) = 130of
Nu wordt door trigonometrie de waarde van de helft van de basis berekend, wat overeenkomt met de helft van de hypotenusa:
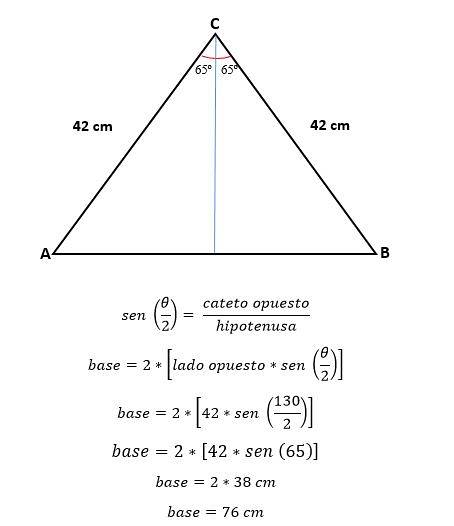
Om het gebied te berekenen, is het nodig om de hoogte van die driehoek te kennen die kan worden berekend door trigonometrie of door de stelling van Pythagoras, nu de waarde van de basis al is bepaald.
Door trigonometrie zal het zijn:

De omtrek wordt berekend:
P = 2(zijde a) + (zijde b).
P = 2 (42 cm) + (76 cm)
P = 84 cm + 76 cm
P = 160 cm.
Derde oefening
Bereken de interne hoeken van de gelijkbenige driehoek, wetende dat de hoek van de basis  = 55 isof
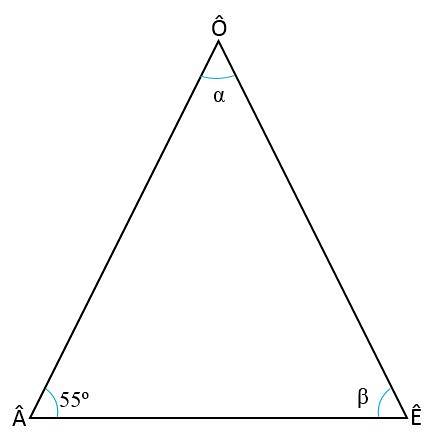
Oplossing
Om de twee ontbrekende hoeken (Ê en Ô) te vinden, is het nodig om twee eigenschappen van driehoeken te onthouden:
- De som van de binnenhoeken van elke driehoek is altijd = 180of
 + Ê + Ô = 180 of
- In een gelijkbenige driehoek zijn de hoeken van de basis altijd congruent, dat wil zeggen, ze hebben dezelfde maat, daarom:
 = Ô
Ê = 55of
Om de waarde van hoek Ê te bepalen, vervangen we de waarden van de andere hoeken in de eerste regel en lossen we Ê op:
55of + 55of + Ô = 180 of
110 of + Ô = 180 of
Ô = 180 of - 110 of
Ô = 70 of.
Referenties
- Álvarez, E. (2003). Geometrie-elementen: met talrijke oefeningen en geometrie van het kompas. Universiteit van Medellin.
- Álvaro Rendón, A. R. (2004). Technische tekening: activiteitenboek.
- Angel, A. R. (2007). Elementaire algebra. Pearson Education.
- Arthur Goodman, L. H. (1996). Algebra en trigonometrie met analytische meetkunde. Pearson Education.
- Baldor, A. (1941). Algebra. Havana: Cultuur.
- José Jiménez, L. J. (2006). Wiskunde 2.
- Tuma, J. (1998). Engineering Mathematics Handbook. Wolfram MathWorld.



Niemand heeft nog op dit artikel gereageerd.