
Eigenschappen van vrije vectoren, voorbeelden, oefeningen
De gratis vectoren Het zijn degenen die volledig worden gespecificeerd door hun omvang, hun richting en hun gevoel, zonder dat het nodig is om een toepassingspunt of een bepaalde oorsprong aan te geven.
Omdat op deze manier oneindige vectoren kunnen worden getekend, is een vrije vector geen enkele entiteit, maar een reeks parallelle en identieke vectoren die onafhankelijk zijn van waar ze zijn..
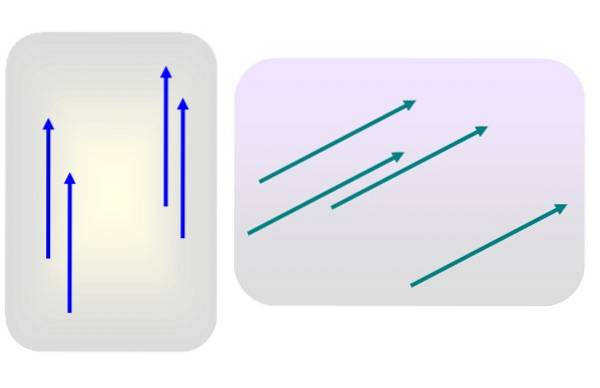
Laten we zeggen dat we verschillende vectoren van magnitude 3 verticaal naar boven gericht hebben, of van magnitude 5 en naar rechts neigen, zoals in figuur 1.
Geen van deze vectoren wordt op enig moment specifiek toegepast. Dan is elk van de blauwe of groene vectoren representatief voor hun respectievelijke groep, aangezien hun karakteristieken - module, richting en gevoel - helemaal niet veranderen wanneer ze naar een andere plaats in het vlak worden overgebracht..
Een vrije vector wordt in gedrukte tekst meestal aangeduid met een vetgedrukte kleine letter, bijvoorbeeld v. Of met kleine letters en een pijl bovenaan als het handgeschreven tekst is.
Artikel index
- 1 Voorbeelden
- 1.1 Eigenschappen en kenmerken
- 2 Opgeloste oefeningen
- 2.1 -Oefening 1
- 2.2 Oefening 2
- 3 referenties
Voorbeelden
Het voordeel van vrije vectoren is dat ze door het vlak of door de ruimte kunnen worden bewogen en hun eigenschappen behouden, aangezien elke vertegenwoordiger van de set even geldig is.
Daarom worden ze in de natuurkunde en mechanica veel gebruikt. Om bijvoorbeeld de lineaire snelheid van een bewegend lichaam aan te geven, is het niet nodig om een bepaald punt op het object te kiezen. De snelheidsvector gedraagt zich dus als een vrije vector.
Een ander voorbeeld van een vrije vector is het krachtenpaar. EEN paar- Het bestaat uit twee krachten van gelijke grootte en richting, maar van tegengestelde richtingen, uitgeoefend op verschillende punten op een vaste stof. Het effect van een paar is niet om het object te vertalen, maar om een rotatie te veroorzaken dankzij de moment geproduceerd.
Figuur 2 toont een aantal krachten die op een stuur worden uitgeoefend. Door de krachten F.1 Y F.twee, Er wordt een koppel gecreëerd dat het vliegwiel rond zijn middelpunt en met de klok mee draait.
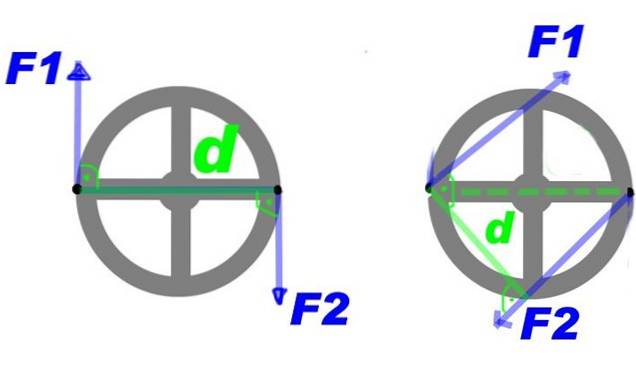
U kunt enkele wijzigingen in het koppel aanbrengen en toch hetzelfde roterende effect krijgen, bijvoorbeeld door de kracht te vergroten, maar de afstand daartussen te verkleinen. Of behoud de kracht en afstand, maar pas het koppel toe op een ander paar punten op het stuur, dat wil zeggen, draai het koppel rond het midden.
Het moment van het paar krachten of gewoon paar-, is een vector waarvan de module Fd en staat loodrecht op het vlak van het vliegwiel. In het voorbeeld dat volgens afspraak wordt weergegeven, heeft de rotatie met de klok mee een negatieve betekenis.
Eigenschappen en kenmerken
In tegenstelling tot de gratis vector v, zijn de vectoren AB Y CD ze staan vast (zie figuur 3), aangezien ze een bepaald startpunt en aankomstpunt hebben. Maar omdat ze teamvriendelijk zijn met elkaar, en op hun beurt met de vector v, zijn representatief voor de gratis vector v.

De belangrijkste eigenschappen van gratis vectoren zijn de volgende:
-Elke vector AB (zie figuur 2) is zoals gezegd representatief voor de vrije vector v.
-De modulus, richting en betekenis zijn hetzelfde in elke vertegenwoordiger van de vrije vector. In Figuur 2 zijn de vectoren AB Y CD vertegenwoordigen de vrije vector v en ze zijn teamgericht.
-Gegeven een punt P in de ruimte, is het altijd mogelijk om een vertegenwoordiger van de vrije vector te vinden v waarvan de oorsprong is in P en genoemde vertegenwoordiger is uniek. Dit is de belangrijkste eigenschap van gratis vectoren en degene die ze zo veelzijdig maakt.
-Een nulvrije vector wordt aangeduid als 0 y is de verzameling van alle vectoren die grootte, richting en gevoel missen.
-Als de vector AB vertegenwoordigt vrije vector v, dan de vector BA vertegenwoordigt vrije vector -v.
-De notatie wordt gebruikt V.3 om de verzameling van alle vrije vectoren van ruimte en aan te duiden V.twee om alle vrije vectoren van het vliegtuig aan te duiden.
Opgeloste oefeningen
Met gratis vectoren kunnen de volgende bewerkingen worden uitgevoerd:
-Som
-Aftrekken
-Vermenigvuldiging van scalair met een vector
-Scalair product tussen twee vectoren.
-Cross product tussen twee vectoren
-Lineaire combinatie van vectoren
En meer.
-Oefening 1
Een leerling probeert van het ene punt aan de oever van een rivier naar het andere daar recht tegenover te zwemmen. Om dit te bereiken, niets direct bij een snelheid van 6 km / u, in een loodrechte richting, maar de stroom heeft een snelheid van 4 km / u die het afbuigt.
Bereken de resulterende snelheid van de zwemmer en hoeveel hij wordt afgebogen door de stroming.
Oplossing
De resulterende snelheid van de zwemmer is de vectorsom van zijn snelheid (ten opzichte van de rivier, verticaal naar boven getekend) en de snelheid van de rivier (van links naar rechts getekend), die wordt uitgevoerd zoals aangegeven in de onderstaande afbeelding:
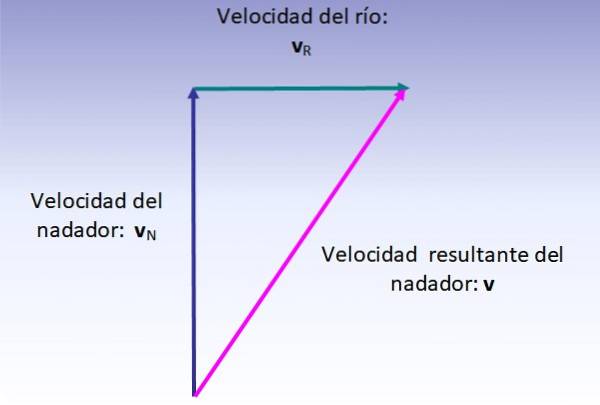
De grootte van de resulterende snelheid komt overeen met de hypotenusa van de weergegeven rechthoekige driehoek, dus:
v = (6twee + 4twee ½ km / u = 7,2 km / u
De richting kan worden berekend met behulp van de hoek ten opzichte van de loodlijn op de kust:
α = arctg (4/6) = 33,7º of 56,3º ten opzichte van de kust.
Oefening 2
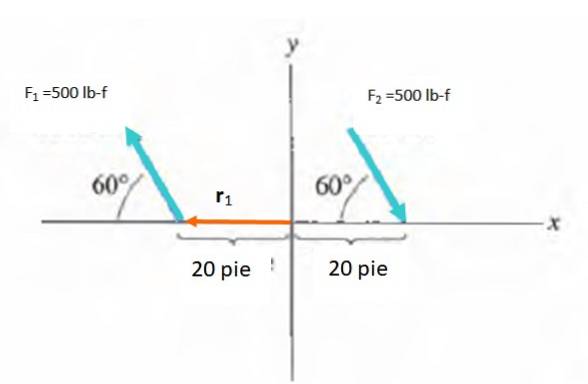
Zoek het moment van het paar dat in de afbeelding wordt weergegeven:
Oplossing
Het moment wordt berekend door:
M. r X F.
De eenheden van dit moment zijn lb-f.ft. Omdat het koppel zich in het vlak van het scherm bevindt, wordt het moment er loodrecht op gericht, naar buiten of naar binnen..
Aangezien het koppel in het voorbeeld de neiging heeft om het object waarop het is aangebracht (wat niet in de afbeelding wordt weergegeven) met de klok mee te draaien, wordt dit moment geacht naar de binnenkant van het scherm te wijzen met een negatief teken..
De grootte van het moment is M = F.d. in a, waarbij a de hoek is tussen de kracht en de vector r. Je moet een punt kiezen om het moment te berekenen, dat is een vrije vector. Daarom is gekozen voor de oorsprong van het referentiesysteem r gaat van O naar het punt waarop elke kracht wordt uitgeoefend.
M.1 = Mtwee = -Fdsen60º = -500. 20 .sin 60º lb-f. ft = -8660,3 lb-f. voet
Het netto moment is de som van M1 en Mtwee: -17329,5 lb-f. voet.
Referenties
- Beardon, T. 2011. Een inleiding tot vectoren. Teruggeplaatst van: nrich.maths.org.
- Bedford, 2000. A. Technische mechanica: statica. Addison Wesley. 38-52.
- Figueroa, D. Series: Physics for Sciences and Engineering. Deel 1. Kinematica 31-68.
- Fysiek. Module 8: Vectoren. Hersteld van: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mechanica voor ingenieurs. Statisch. 6e editie. Continental Publishing Company. 15-53.
- Vector Toevoeging Calculator. Hersteld van: 1728.org
- Vectoren. Hersteld van: en.wikibooks.org


Niemand heeft nog op dit artikel gereageerd.