
Hoeksnelheidsdefinitie, formule, berekening en oefeningen
De hoeksnelheid is een maat voor de rotatiesnelheid en wordt gedefinieerd als de hoek waarin de positievector van het roterende object roteert, per tijdseenheid. Het is een omvang die heel goed de beweging beschrijft van een veelvoud aan objecten die constant overal ronddraaien: cd's, autowielen, machines, de aarde en nog veel meer..
Een diagram van het "London eye" is te zien in de volgende afbeelding. Het vertegenwoordigt de beweging van een passagier vertegenwoordigd door punt P, dat het cirkelvormige pad volgt, genaamd c:
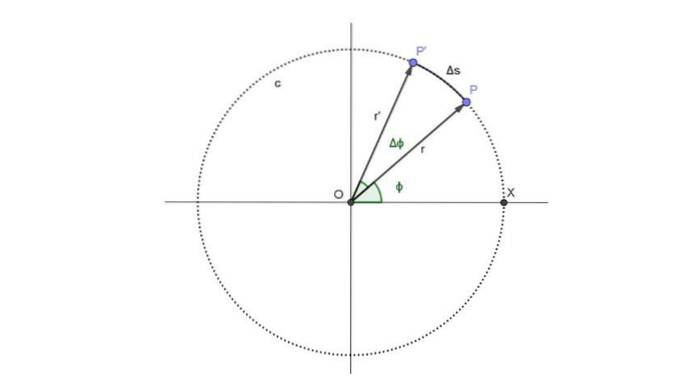
De passagier bezet positie P op moment t en de hoekpositie die overeenkomt met dat moment is ϕ.
Vanaf het moment t verstrijkt een tijdsperiode Δt. In deze periode is de nieuwe positie van de punctuele passagier P 'en is de hoekpositie vergroot met een hoek Δ increased.
Artikel index
- 1 Hoe bereken je de hoeksnelheid ?
- 1.1 Verband tussen lineaire en hoeksnelheid
- 2 Uniforme rotatiebeweging
- 3 Opgeloste problemen van hoeksnelheid
- 3.1 Oefening 1
- 4 Oefening 2
- 4.1 Oefening 3
- 4.2 Oefening 4
- 5 referenties
Hoe bereken je de hoeksnelheid ?
Voor roterende grootheden worden Griekse letters veel gebruikt om ze te onderscheiden van lineaire grootheden. Dus in eerste instantie definiëren we de gemiddelde hoeksnelheid ωm als de hoek die in een bepaalde tijd is afgelegd.
Dan vertegenwoordigt het quotiënt Δϕ / Δt de gemiddelde hoeksnelheid ωm tussen tijden t en t + Δt.
Als u de hoeksnelheid juist op het moment t, dan zullen we het quotiënt Δϕ / Δt moeten berekenen als Δt ➡0:

Verband tussen lineaire en hoeksnelheid
Lineaire snelheid v, is het quotiënt tussen de afgelegde afstand en de tijd die nodig is om deze af te leggen.
In de bovenstaande afbeelding is de afgelegde boog Δs. Maar die boog is evenredig met de afgelegde hoek en de straal, waarbij aan de volgende relatie wordt voldaan, die geldig is zolang Δϕ wordt gemeten in radialen:
Δs = r ・ Δϕ
Als we de vorige uitdrukking delen door de tijdsverloop Δt en de limiet nemen als Δt ➡0, krijgen we:
v = r ・ ω
Uniforme rotatiebeweging

Een rotatiebeweging is uniform als op elk waargenomen moment de afgelegde hoek dezelfde is in dezelfde tijdsperiode.
Als de rotatie uniform is, valt de hoeksnelheid op elk moment samen met de gemiddelde hoeksnelheid.

Bovendien is de afgelegde hoek 2π (gelijk aan 360º) wanneer een volledige bocht is gemaakt. Daarom is in een uniforme rotatie de hoeksnelheid ω gerelateerd aan de periode T, door de volgende formule:

f = 1 / T
Met andere woorden, bij een uniforme rotatie is de hoeksnelheid gerelateerd aan de frequentie door:
ω = 2π ・ f
Problemen met hoeksnelheid opgelost
Oefening 1
De cabines van het grote draaiende wiel dat bekend staat als de 'London Eye”Ze bewegen langzaam. De snelheid van de cabines is 26 cm / s en het wiel heeft een diameter van 135 m.
Bereken met deze gegevens:
i) De hoeksnelheid van het wiel
ii) De frequentie van rotatie
iii) De tijd die een hut nodig heeft om een volledige bocht te maken.
Antwoorden:
ik) De snelheid v in m / s is: v = 26 cm / s = 0,26 m / s.
De straal is de helft van de diameter: r = (135 m) / 2 = 67,5 m
v = r ・ ω => ω = v / r = (0,26 m / s) / (67,5 m) = 0,00385 rad / s
ii) ω = 2π ・ f => f = ω / 2π = (0,00385 rad / s) / (2π rad) = 6,13 x 10-4 beurten / s
f = 6,13 x 10 ^ -4 omwentelingen / s = 0,0368 omwentelingen / min = 2,21 omwentelingen / uur.
iii) T = 1 / f = 1 / 2,21 ronde / uur = 0,45311 uur = 27 min 11 sec
Oefening 2
Een speelgoedauto rijdt op een cirkelvormige baan met een straal van 2 meter. Op 0 s is zijn hoekpositie 0 rad, maar na een tijd t wordt zijn hoekpositie gegeven door:
φ (t) = 2 ・ t
Bepalen:
i) De hoeksnelheid
ii) De lineaire snelheid op elk moment.
Antwoorden:
ik) De hoeksnelheid is de afgeleide van de hoekpositie: ω = φ '(t) = 2.
Dat wil zeggen, de speelgoedauto heeft te allen tijde een constante hoeksnelheid gelijk aan 2 rad / s.
ii) De lineaire snelheid van de auto is: v = r ・ ω = 2 m ・ 2 rad / s = 4 m / s = 14,4 Km / h
Oefening 3
Dezelfde auto uit de vorige oefening begint te stoppen. Zijn hoekpositie als functie van de tijd wordt gegeven door de volgende uitdrukking:
φ (t) = 2 ・ t - 0,5 ・ ttwee
Bepalen:
i) De hoeksnelheid op elk moment
ii) De lineaire snelheid op elk moment
iii) De tijd die nodig is om te stoppen vanaf het moment dat het begint te vertragen
iv) De afgelegde hoek
v) afgelegde afstand
Antwoorden:
ik) De hoeksnelheid is de afgeleide van de hoekpositie: ω = φ '(t)
ω (t) = φ '(t) = (2 ・ t - 0,5 ・ ttwee) '= 2 - t
ii) De lineaire snelheid van de auto op elk moment wordt gegeven door:
v (t) = r ・ ω (t) = 2 ・ (2 - t) = 4 - 2 t
iii) De tijd die nodig is om te stoppen vanaf het moment dat het begint te vertragen, wordt bepaald door het moment te kennen waarop de snelheid v (t) nul wordt.
v (t) = 4 - 2 t = 0 => t = 2
Dat wil zeggen, hij stopt 2 seconden nadat hij is begonnen met remmen.
iv) In de periode van 2 seconden vanaf het moment dat het begint te remmen tot het stopt, wordt een hoek gegeven door φ (2) afgelegd:
φ (2) = 2 ・ 2 - 0,5 ・ 2 ^ 2 = 4 - 2 = 2 rad = 2 x 180 / π = 114,6 graden
v) In de periode van 2 s vanaf het moment dat het begint te remmen tot het stoppen, een afstand s gegeven door:
s = r ・ φ = 2m ・ 2 rad = 4 m
Oefening 4
De wielen van een auto hebben een diameter van 80 cm. Als de auto 100 km / u rijdt. Zoek: i) de rotatiesnelheid van de wielen, ii) de rotatiefrequentie van de wielen, iii) het aantal omwentelingen dat het wiel maakt tijdens een reis van 1 uur.
Antwoorden:
ik) Eerst gaan we de snelheid van de auto omrekenen van Km / u naar m / s
v = 100 km / u = (100 / 3,6) m / s = 27,78 m / s
De rotatiesnelheid van de wielen wordt gegeven door:
ω = v / r = (27,78 m / s) / (0,4 m) = 69,44 rad / s
ii) De rotatiefrequentie van de wielen wordt gegeven door:
f = ω / 2π = (69,44 rad / s) / (2π rad) = 11,05 draai / s
De rotatiefrequentie wordt meestal uitgedrukt in omwentelingen per minuut tpm.
f = 11,05 omwentelingen / s = 11,05 omwentelingen / (1/60) min = 663,15 omwentelingen per minuut
iii) Het aantal ronden dat het wiel maakt in een rit van 1 uur wordt berekend wetende dat 1 uur = 60 min en dat de frequentie het aantal ronden N gedeeld door de tijd waarin die N ronden zijn gemaakt.
f = N / t => N = f ・ t = 663,15 (beurten / min) x 60 min = 39788,7 beurten.
Referenties
- Giancoli, D. Physics. Principes met toepassingen. 6e editie. Prentice Hall. 106-108.
- Resnick, R. (1999). Fysiek. Deel 1. Derde editie in het Spaans. Mexico. Compañía Redactioneel Continental S.A. de C.V. 67-69.
- Serway, R., Jewett, J. (2008). Physics for Science and Engineering. Deel 1. 7e. Editie. Mexico. Cengage Learning Editors. 84-85.
- geogebra.org


Niemand heeft nog op dit artikel gereageerd.