De atomair volume is een relatieve waarde die de relatie aangeeft tussen de molaire massa van een element en zijn dichtheid. Dit volume hangt dus af van de dichtheid van het element, en de dichtheid hangt op zijn beurt af van de fase en hoe de atomen erin zijn gerangschikt..
Het atomaire volume van een element Z is dus niet hetzelfde in een andere fase dan degene die het vertoont bij kamertemperatuur (vloeibaar, vast of gasvormig), of wanneer het deel uitmaakt van bepaalde verbindingen. Het atomaire volume van Z in verbinding ZA is dus anders dan dat van Z in verbinding ZB.
Waarom? Om het te begrijpen, is het nodig om atomen te vergelijken met bijvoorbeeld knikkers. De knikkers hebben, net als de blauwachtige in de bovenstaande afbeelding, een zeer goed gedefinieerde materiaalrand, die te zien is dankzij hun glanzende oppervlak. De grens van de atomen daarentegen is diffuus, hoewel ze op afstand als bolvormig kunnen worden beschouwd.
Wat dus een punt buiten de atomaire grens bepaalt, is de nulkans om een elektron te vinden, en dit punt kan verder of dichter bij de kern liggen, afhankelijk van het aantal naburige atomen rond het betreffende atoom..
Artikel index
Door interactie tussen twee H-atomen in het H-molecuultwee, de posities van hun kernen worden gedefinieerd, evenals de afstanden tussen hen (internucleaire afstanden). Als beide atomen bolvormig zijn, is de straal de afstand tussen de kern en de vage grens:
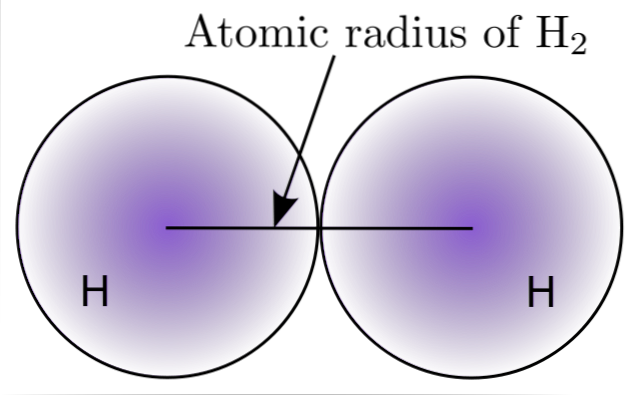
In de afbeelding hierboven kun je zien hoe de kans om een elektron te vinden afneemt naarmate het zich van de kern verwijdert. Door de internucleaire afstand door twee te delen, wordt de atoomstraal verkregen. Vervolgens, uitgaande van een sferische geometrie voor de atomen, wordt de formule gebruikt om het volume van een bol te berekenen:
V = (4/3) (Pi) r3
In deze uitdrukking is r de atoomstraal bepaald voor het H-molecuultwee. De waarde van V berekend met deze onnauwkeurige methode kan veranderen als bijvoorbeeld H in aanmerking wordt genomentwee in vloeibare of metallische toestand. Deze methode is echter erg onnauwkeurig omdat de vormen van de atomen ver verwijderd zijn van de ideale sfeer in hun interacties..
Om de atomaire volumes in vaste stoffen te bepalen, wordt rekening gehouden met veel variabelen met betrekking tot de rangschikking, die worden verkregen door röntgendiffractiestudies..
Molaire massa drukt de hoeveelheid materie uit die een mol atomen van een chemisch element heeft.
De eenheden zijn g / mol. Aan de andere kant is dichtheid het volume dat één gram van het element inneemt: g / ml. Omdat de eenheden van atomair volume ml / mol zijn, moet je met de variabelen spelen om tot de gewenste eenheden te komen:
(g / mol) (ml / g) = ml / mol
Of wat is hetzelfde:
(Molaire massa) (1 / D) = V
(Molaire massa / D) = V
Zo kan het volume van één mol atomen van een element gemakkelijk worden berekend; terwijl met de formule van het bolvormige volume het volume van een individueel atoom wordt berekend. Om vanaf de eerste waarde tot deze waarde te komen, is een conversie nodig via het nummer van Avogadro (6.02 · 10-2. 3.
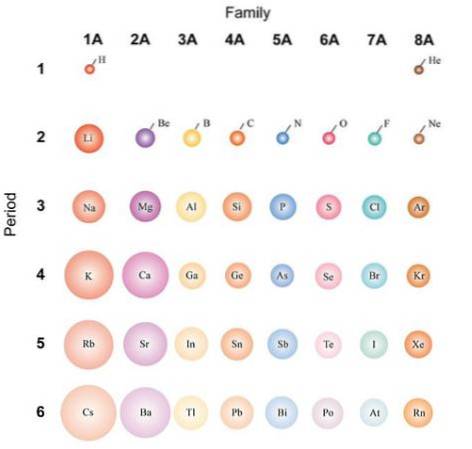
Als de atomen als bolvormig worden beschouwd, zal hun variatie dezelfde zijn als die wordt waargenomen in atoomstralen. In de afbeelding hierboven, die representatieve elementen toont, wordt geïllustreerd dat van rechts naar links de atomen kleiner worden; in plaats daarvan worden ze van boven naar beneden volumineuzer.
Dit komt omdat in dezelfde periode de kern protonen opneemt terwijl deze naar rechts beweegt. Deze protonen oefenen een aantrekkingskracht uit op de externe elektronen, die een effectieve nucleaire lading Z voelenef, minder dan de werkelijke nucleaire lading Z.
De elektronen van de binnenste schil stoten die van de buitenste schil af, waardoor het effect van de kern op hen wordt verminderd; dit staat bekend als het schermeffect. In dezelfde periode kan het schermeffect de toename van het aantal protonen niet tegengaan, dus de elektronen in de binnenschil verhinderen niet dat de atomen samentrekken..
Afdalen in een groep maakt echter nieuwe energieniveaus mogelijk, waardoor elektronen verder van de kern kunnen cirkelen. Evenzo neemt het aantal elektronen in de binnenschil toe, waarvan de afschermende effecten beginnen af te nemen als de kern weer protonen toevoegt..
Om deze redenen wordt erkend dat groep 1A de meest volumineuze atomen heeft, in tegenstelling tot de kleine atomen van groep 8A (of 18), die van de edelgassen..
Overgangsmetaalatomen nemen elektronen op in binnenste d-orbitalen. Deze toename van het schermeffect en, evenals van de werkelijke nucleaire lading Z, heffen bijna evenveel op, zodat hun atomen in dezelfde periode een vergelijkbare grootte behouden..
Met andere woorden: in één periode vertonen overgangsmetalen vergelijkbare atomaire volumes. Deze kleine verschillen zijn echter enorm significant bij het definiëren van metalen kristallen (alsof het metalen knikkers zijn).
Er zijn twee wiskundige formules beschikbaar om het atomaire volume van een element te berekenen, elk met bijbehorende voorbeelden.
Gezien de atoomstraal van waterstof -37 pm (1 picometer = 10-12m) - en cesium -265 pm-, berekenen hun atomaire volumes.
Met behulp van de bolvormige volumeformule hebben we dan:
V.H.= (4/3) (3.14) (37 uur)3= 212.07 uur3
V.Cs= (4/3) (3.14) (265 uur)3= 77912297.67 uur3
Deze volumes uitgedrukt in picometers zijn echter exorbitant, dus worden ze omgezet in eenheden van ångström, vermenigvuldigd met de omrekeningsfactor (1Å / 100pm)3
(212.07 uur3) (1 A / 100 uur)3= 2.1207 × 10-4 NAAR3
(77912297.67 uur3) (1 A / 100 uur)3= 77,912 A3
De verschillen in grootte tussen het kleine H-atoom en het omvangrijke Cs-atoom worden dus numeriek aangetoond. Houd er rekening mee dat deze berekeningen slechts benaderingen zijn onder de stelling dat een atoom volledig bolvormig is, dat voor de werkelijkheid dwaalt.
De dichtheid van puur goud is 19,32 g / ml en de molaire massa is 196,97 g / mol. Door de M / D-formule toe te passen om het volume van één mol goudatomen te berekenen, wordt het volgende verkregen:
V.Au= (196,97 g / mol) / (19,32 g / ml) = 10,19 ml / mol
Dat wil zeggen, 1 mol goudatomen beslaat 10,19 ml, maar welk volume neemt een goudatoom specifiek in? En hoe het uit te drukken in eenheden van pm3? Pas hiervoor gewoon de volgende omrekenfactoren toe:
(10,19 ml / mol) · (mol / 6,02 · 10-2. 3 atomen) · (1 m / 100 cm)3(13.00 uur / 10-12m)3= 16,92 · 106 p.m3
Aan de andere kant is de atoomstraal van goud 166 pm. Als beide volumes worden vergeleken - degene die is verkregen met de vorige methode en degene die is berekend met de bolvormige volumeformule - zal blijken dat ze niet dezelfde waarde hebben:
V.Au= (4/3) (3.14) (166 uur)3= 19,15 · 106 p.m3
Welke van de twee ligt het dichtst bij de geaccepteerde waarde? Degene die het dichtst in de buurt komt van de experimentele resultaten die zijn verkregen door röntgendiffractie van de kristalstructuur van goud.
Niemand heeft nog op dit artikel gereageerd.