
Gepoolde gegevensvoorbeelden en oefening opgelost
De gegroepeerde gegevens zijn die welke zijn ingedeeld in categorieën of klassen, waarbij hun frequentie als criterium wordt genomen. Dit wordt gedaan om de verwerking van grote hoeveelheden gegevens te vereenvoudigen en de trends vast te stellen..
Eenmaal georganiseerd in deze klassen op basis van hun frequentie, vormen de gegevens een frequentieverdeling, waaruit via zijn kenmerken nuttige informatie wordt gehaald.

Hier is een eenvoudig voorbeeld van gegroepeerde gegevens:
Stel dat de lengte van 100 vrouwelijke studenten, geselecteerd uit alle basisvakken natuurkunde van een universiteit, wordt gemeten en de volgende resultaten worden behaald:

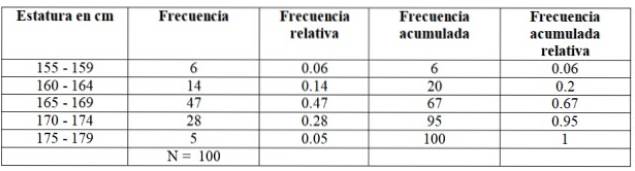
De verkregen resultaten zijn onderverdeeld in 5 klassen, die in de linkerkolom verschijnen.
De eerste klas, tussen 155 en 159 cm, heeft 6 leerlingen, de tweede klas 160 - 164 cm heeft 14 leerlingen, de derde klas van 165 tot 169 cm heeft het grootste aantal leden: 47. Daarna gaat de klas verder 170-174 cm met 28 leerlingen en tenslotte de 175-174 cm met slechts 5.
Het aantal leden van elke klas is precies het frequentie of Absolute frequentie en als je ze allemaal optelt, wordt de totale data verkregen, die in dit voorbeeld 100 is.
Artikel index
- 1 Kenmerken van de frequentieverdeling
- 1.1 Frequentie
- 1.2 Limieten
- 1.3 Grenzen
- 1.4 amplitude
- 1.5 Klassenmerk
- 2 Maatregelen van centrale tendens en spreiding voor gegroepeerde gegevens
- 2,1 gemiddeld
- 2.2 Mediaan
- 2.3 Mode
- 2.4 Variantie en standaarddeviatie
- 3 Oefening opgelost
- 3.1 Oplossing a
- 3.2 Oplossing b
- 3.3 Oplossing d
- 4 referenties
Kenmerken van de frequentieverdeling
Frequentie
Zoals we hebben gezien, is de frequentie het aantal keren dat een gegevensstuk wordt herhaald. En om de berekeningen van de eigenschappen van de verdeling, zoals het gemiddelde en de variantie, te vergemakkelijken, worden de volgende grootheden gedefinieerd:
-Cumulatieve frequentie: het wordt verkregen door de frequentie van een klasse toe te voegen aan de vorige geaccumuleerde frequentie. De eerste van alle frequenties komt overeen met die van het betreffende interval en de laatste is het totale aantal gegevens.
-Relatieve frequentie: berekend door de absolute frequentie van elke klasse te delen door het totale aantal gegevens. En als je vermenigvuldigt met 100, heb je de relatieve frequentie in percentage.
-Cumulatieve relatieve frequentie: is de som van de relatieve frequenties van elke klasse met de vorige opgeteld. De laatste van de verzamelde relatieve frequenties moet gelijk zijn aan 1.
Voor ons voorbeeld zien de frequenties er als volgt uit:
Grenzen
De extreme waarden van elke klasse of interval worden aangeroepen klasse limieten. Zoals we kunnen zien, heeft elke klasse een lagere en een hogere limiet. Zo heeft de eerste klas in de studie over hoogtes een ondergrens van 155 cm en een bovengrens van 159 cm..
Dit voorbeeld heeft limieten die duidelijk zijn gedefinieerd, maar het is mogelijk om open limieten te definiëren: als in plaats van de exacte waarden te definiëren, zeg 'hoogte minder dan 160 cm', 'hoogte minder dan 165 cm' enzovoort.
Grenzen
Hoogte is een continue variabele, dus kan worden aangenomen dat de eerste klas eigenlijk begint bij 154,5 cm, aangezien het afronden van deze waarde op het dichtstbijzijnde gehele getal 155 cm oplevert.
Deze klasse omvat alle waarden tot 159,5 cm, want daarna worden de hoogtes afgerond op 160,0 cm. Een hoogte van 159,7 cm behoort al tot de volgende klasse.
De werkelijke klassengrenzen voor dit voorbeeld zijn in cm:
- 154,5 - 159,5
- 159,5 - 164,5
- 164,5 - 169,5
- 169,5 - 174,5
- 174,5 - 179,5
Amplitude
De breedte van een klasse wordt verkregen door de grenzen af te trekken. Voor het eerste interval van ons voorbeeld hebben we 159,5 - 154,5 cm = 5 cm.
De lezer kan verifiëren dat voor de andere intervallen van het voorbeeld de amplitude ook 5 cm is. Er moet echter worden opgemerkt dat verdelingen kunnen worden geconstrueerd met intervallen van verschillende amplitude.
Klasse merk
Het is het middelpunt van het interval en wordt verkregen door het gemiddelde tussen de bovengrens en de ondergrens.
Voor ons voorbeeld is het eerste klasmerk (155 + 159) / 2 = 157 cm. De lezer kan zien dat de overige klassencijfers zijn: 162, 167, 172 en 177 cm.
Het bepalen van de klassencijfers is belangrijk, omdat ze nodig zijn om het rekenkundig gemiddelde en de variantie van de verdeling te vinden.
Maatregelen van centrale tendens en spreiding voor gepoolde gegevens
De meest gebruikte maten van centrale tendens zijn het gemiddelde, de mediaan en de modus, en ze beschrijven precies de neiging van de gegevens om rond een bepaalde centrale waarde te clusteren..
Voor de helft
Het is een van de belangrijkste maatregelen van centrale tendens. In de gegroepeerde gegevens kan het rekenkundig gemiddelde worden berekend met behulp van de formule:

-X is het gemiddelde
-F.ik is de frequentie van de klas
-mik is het klassenteken
-g is het aantal klassen
-n is het totale aantal gegevens
Mediaan
Voor de mediaan is het nodig om het interval te identificeren waar de waarneming n / 2 wordt gevonden. In ons voorbeeld is deze waarneming nummer 50, omdat er in totaal 100 gegevenspunten zijn. Deze waarneming ligt in het bereik van 165-169 cm.
Dan moet je interpoleren om de numerieke waarde te vinden die overeenkomt met die waarneming, waarvoor de formule wordt gebruikt:

Waar:
-c = breedte van het interval waar de mediaan wordt gevonden
-B.M. = de ondergrens van het interval waartoe de mediaan behoort
-F.m = aantal waarnemingen in het mediaan interval
-n / 2 = de helft van de totale gegevens
-F.BM = totaal aantal waarnemingen voordat mediaan interval
mode
Voor de modus wordt de modale klasse geïdentificeerd, degene die de meeste waarnemingen bevat, waarvan het klassemarkering bekend is.
Variantie en standaarddeviatie
De variantie en standaarddeviatie zijn maatstaven voor spreiding. Als we de variantie aangeven met stwee en de standaarddeviatie, die de vierkantswortel is van de variantie als s, voor gegroepeerde gegevens hebben we respectievelijk:

Y

Oefening opgelost
Bereken voor de in het begin voorgestelde lengteverdeling van vrouwelijke universiteitsstudenten de waarden van:
a) Gemiddeld
b) Mediaan
c) Mode
d) Variantie en standaarddeviatie.

Oplossing voor
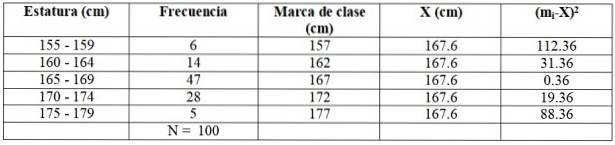
Laten we de volgende tabel bouwen om de berekeningen te vergemakkelijken:


Waarden vervangen en de sommatie direct uitvoeren:
X = (6 x 157 + 14 x 162 + 47 x 167 + 28 x 172+ 5 x 177) / 100 cm =
= 167,6 cm
Oplossing b
Het interval waartoe de mediaan behoort, is 165-169 cm omdat dit het interval is met de hoogste frequentie.

Laten we elk van deze waarden in het voorbeeld identificeren met behulp van tabel 2:
c = 5 cm (zie het gedeelte over amplitude)
B.M. = 164,5 cm
F.m = 47
n / 2 = 100/2 = 50
F.BM = 20
Vervanging in de formule:
Het interval dat de meeste waarnemingen bevat is 165-169 cm, waarvan het klassenteken 167 cm is.
Oplossing d
We breiden de vorige tabel uit door twee extra kolommen toe te voegen:

We passen de formule toe:

En we ontwikkelen de sommatie:
stwee = (6 x 112,36 + 14 x 31,36 + 47 x 0,36 + 28 x 19,36 + 5 x 88,36) / 99 = = 21,35 cmtwee
Daarom:
s = √21,35 cmtwee = 4,6 cm
Referenties
- Berenson, M. 1985. Statistieken voor management en economie. Interamericana S.A.
- Canavos, G. 1988. Waarschijnlijkheid en statistiek: toepassingen en methoden. Mcgraw heuvel.
- Devore, J. 2012. Waarschijnlijkheid en statistiek voor techniek en wetenschap. 8e. Editie. Cengage.
- Levin, R. 1988. Statistieken voor beheerders. 2e. Editie. Prentice hal.
- Spiegel, M. 2009. Statistieken. Schaum-serie. 4e Editie. Mcgraw heuvel.
- Walpole, R. 2007. Waarschijnlijkheid en statistiek voor techniek en wetenschappen. Pearson.



Niemand heeft nog op dit artikel gereageerd.