De additieve ontleding van een positief geheel getal is om het uit te drukken als een som van twee of meer positieve gehele getallen. We hebben dus dat het getal 5 kan worden uitgedrukt als 5 = 1 + 4, 5 = 2 + 3 of 5 = 1 + 2 + 2. Elk van deze manieren om het nummer 5 te schrijven, is wat we additieve ontleding zullen noemen.
Als we opletten, kunnen we zien dat de uitdrukkingen 5 = 2 + 3 en 5 = 3 + 2 dezelfde compositie vertegenwoordigen; ze hebben allebei dezelfde nummers. Gemakshalve wordt echter elk van de addends gewoonlijk geschreven volgens het criterium van laag naar hoog.
Artikel index
Als een ander voorbeeld kunnen we het getal 27 nemen, dat we kunnen uitdrukken als:
27 = 7 + 10 + 10
27 = 9 + 9 + 9
27 = 3 + 6 + 9 + 9
27 = 9 + 18
Additieve ontleding is een zeer nuttige tool waarmee we onze kennis van nummeringsystemen kunnen versterken.
Als we getallen hebben met meer dan twee cijfers, is een bepaalde manier om ze te ontbinden in de veelvouden van 10, 100, 1000, 10 000, enz., Waaruit het bestaat. Deze manier van schrijven van elk nummer wordt canonieke additieve ontleding genoemd. Het getal 1456 kan bijvoorbeeld als volgt worden ontleed:
1456 = 1000 + 400+ 50 + 6
Als we het nummer 20846295 hebben, is de canonieke additieve ontleding:
20846295 = 20.000.000 + 800.000 + 40.000 + 6000 + 200 + 90 +5.
Dankzij deze ontleding kunnen we zien dat de waarde van een bepaald cijfer wordt gegeven door de positie die het inneemt. Laten we de nummers 24 en 42 als voorbeeld nemen:
24 = 20 + 4
42 = 40 +2
Hier kunnen we zien dat in 24 de 2 een waarde heeft van 20 eenheden en de 4 een waarde van 4 eenheden; aan de andere kant heeft in 42 de 4 een waarde van 40 eenheden en de 2 van twee eenheden. Dus hoewel beide nummers dezelfde cijfers gebruiken, zijn hun waarden totaal verschillend vanwege de positie die ze innemen.
Een van de toepassingen die we kunnen geven aan additieve ontleding is in bepaalde soorten bewijzen, waarin het erg handig is om een positief geheel getal te zien als de som van andere.
Laten we als voorbeeld de volgende stelling nemen met zijn respectievelijke bewijzen.
- Laat Z een geheel getal van 4 cijfers zijn, dan is Z deelbaar door 5 als het eenheidsnummer nul of vijf is.
Laten we onthouden wat deelbaarheid is. Als we gehele getallen "a" en "b" hebben, zeggen we dat "a" "b" deelt als er een geheel getal "c" is, zodat b = a * c.
Een van de eigenschappen van deelbaarheid vertelt ons dat als "a" en "b" deelbaar zijn door "c", de aftrekking "a-b" ook deelbaar is..
Laat Z een geheel getal van 4 cijfers zijn; daarom kunnen we Z schrijven als Z = ABCD.
Met behulp van canonieke additieve ontleding hebben we:
Z = A * 1000 + B * 100 + C * 10 + D
Het is duidelijk dat A * 1000 + B * 100 + C * 10 deelbaar is door 5. Om deze reden hebben we dat Z deelbaar is door 5 als Z - (A * 1000 + B * 100 + C * 10) deelbaar is door 5.
Maar Z - (A * 1000 + B * 100 + C * 10) = D en D is een getal van één cijfer, dus de enige manier waarop het deelbaar is door 5 is dat het 0 of 5 is.
Daarom is Z deelbaar door 5 als D = 0 of D = 5.
Merk op dat als Z n cijfers heeft, het bewijs exact hetzelfde is, het verandert alleen dat we nu Z = A schrijven1NAARtwee… NAARn en het doel zou zijn om te bewijzen dat An het is nul of vijf.
We zeggen dat een partitie van een positief geheel getal een manier is waarop we een getal kunnen schrijven als een som van positieve gehele getallen.
Het verschil tussen een additieve ontleding en een scheidingswand is dat, terwijl de eerste probeert dat deze tenminste kan worden ontleed in twee of meer toevoegingen, de scheidingswand deze beperking niet heeft.
We hebben dus het volgende:
5 = 5
5 = 1 + 4
5 = 2 + 3
5 = 1 + 2 + 2
Het bovenstaande zijn partities van 5.
Dat wil zeggen, we hebben dat elke additieve ontleding een partitie is, maar niet elke partitie is noodzakelijkerwijs een additieve ontleding..
In de getaltheorie, de fundamentele stelling van rekenkunde garandeert dat elk geheel getal uniek kan worden geschreven als een product van priemgetallen.
Bij het bestuderen van partities is het doel om te bepalen op hoeveel manieren een positief geheel getal kan worden geschreven als de som van andere gehele getallen. Daarom definiëren we de partitiefunctie zoals hieronder weergegeven.
De partitiefunctie p (n) wordt gedefinieerd als het aantal manieren waarop een positief geheel getal n kan worden geschreven als een som van positieve gehele getallen.
Terugkerend naar het voorbeeld van 5, hebben we dat:
5 = 5
5 = 1 + 4
5 = 2 + 3
5 = 1 + 1 + 3
5 = 1 + 2 + 2
5 = 1 + 1 + 1 + 2
5 = 1 + 1 + 1 + 1 + 1
Dus p (5) = 7.
Zowel partities als additieve decomposities van een getal n kunnen geometrisch worden weergegeven. Stel dat we een additieve ontleding hebben van n. Bij deze decompositie kunnen de bijlagen zo worden gerangschikt dat de leden van de som worden geordend van klein naar groot. Dus oke:
n = een1 + naartwee + naar3 +… + Ar met
naar1 ≤ eentwee ≤ een3 ≤… ≤ ar.
We kunnen deze decompositie op de volgende manier in kaart brengen: in een eerste rij markeren we de a1-punten, dan markeren we in de volgendetwee-punten, enzovoort, totdat u eenr.
Neem bijvoorbeeld het getal 23 en de volgende decompositie:
23 = 5 + 4 + 7 + 3 + 1 +3
We bestellen deze ontbinding en we hebben:
23 = 1 + 3 + 3 + 4+ 5 + 7
De bijbehorende grafiek zou zijn:
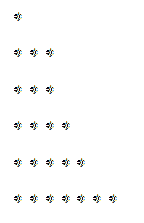
Evenzo, als we de genoemde grafiek verticaal in plaats van horizontaal lezen, kunnen we een decompositie verkrijgen die mogelijk anders is dan de vorige. In het voorbeeld van 23 valt het volgende op:
Dus we hebben er 23, we kunnen het ook schrijven als:
23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.
Niemand heeft nog op dit artikel gereageerd.