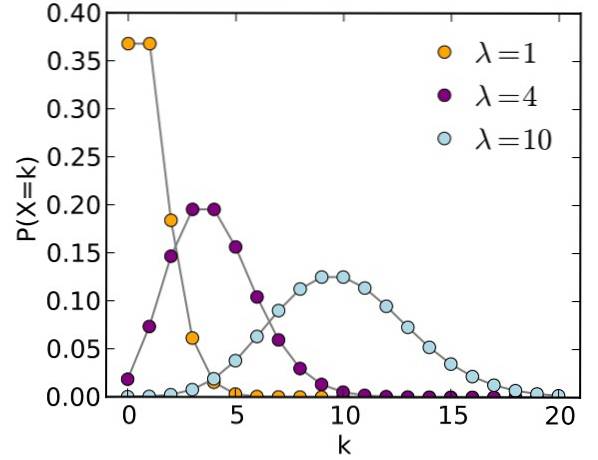
De Poisson-verdeling is een discrete kansverdeling, waardoor het mogelijk is om de kans te kennen dat, binnen een grote steekproefomvang en gedurende een bepaald interval, een gebeurtenis plaatsvindt waarvan de kans klein is.
Vaak kan de Poisson-verdeling worden gebruikt in plaats van de binominale verdeling, zolang aan de volgende voorwaarden wordt voldaan: grote steekproef en kleine kans.
Siméon-Denis Poisson (1781-1840) creëerde deze distributie die zijn naam draagt, erg handig als het gaat om onvoorspelbare gebeurtenissen. Poisson publiceerde zijn resultaten in 1837, een onderzoek naar de waarschijnlijkheid van onjuiste strafrechtelijke straffen.
Later pasten andere onderzoekers de verdeling in andere gebieden aan, bijvoorbeeld het aantal sterren dat in een bepaald volume van de ruimte te vinden was, of de kans dat een soldaat stierf door de trap van een paard..
Artikel index
De wiskundige vorm van de Poisson-verdeling is als volgt:
- μ (ook wel aangeduid als λ) is het gemiddelde of de parameter van de verdeling
- Euler-nummer: e = 2,71828
- De kans om y = k te verkrijgen is P
- k is het aantal successen 0, 1,2,3 ...
- n is het aantal tests of evenementen (de steekproefomvang)
Discrete willekeurige variabelen, zoals hun naam aangeeft, zijn afhankelijk van het toeval en nemen alleen discrete waarden aan: 0, 1, 2, 3, 4 ..., k.
Het gemiddelde van de verdeling wordt gegeven door:
De variantie σ, die de spreiding van de gegevens meet, is een andere belangrijke parameter. Voor de Poisson-verdeling is het:
σ = μ
Poisson stelde vast dat wanneer n → ∞, en p → 0, de gemiddelde μ -ook wordt aangeroepen verwachte waarde- neigt naar een constante:
μ → constant
Belangrijk p is de kans dat de gebeurtenis zich voordoet, rekening houdend met de totale populatie, terwijl P (y) is de Poisson-voorspelling op de steekproef.
De Poisson-verdeling heeft de volgende eigenschappen:
-De steekproefomvang is groot: n → ∞.
-De beschouwde gebeurtenissen of gebeurtenissen zijn onafhankelijk van elkaar en vinden willekeurig plaats.
-Waarschijnlijkheid P. dat bepaalde evenement Y treedt op tijdens een bepaalde periode is erg klein: P → 0.
-De kans dat er meer dan één gebeurtenis plaatsvindt in het tijdsinterval is 0.
-De gemiddelde waarde benadert een constante gegeven door: μ = n.p (n is de steekproefomvang
-Omdat de spreiding σ gelijk is aan μ, naarmate deze grotere waarden aanneemt, wordt de variabiliteit ook groter.
-De gebeurtenissen moeten gelijkmatig worden verdeeld over het gebruikte tijdsinterval.
-De set van mogelijke gebeurteniswaarden Y is: 0,1,2,3,4 ... .
-De som van ik variabelen die een Poisson-verdeling volgen, is ook een andere Poisson-variabele. De gemiddelde waarde is de som van de gemiddelde waarden van deze variabelen.
De Poisson-verdeling verschilt op de volgende belangrijke manieren van de binominale verdeling:
-De binominale verdeling wordt beïnvloed door zowel de steekproefomvang n als de waarschijnlijkheid P., maar de Poisson-verdeling wordt alleen beïnvloed door het gemiddelde μ.
-In een binominale verdeling, de mogelijke waarden van de willekeurige variabele Y zijn 0,1,2,…, N, aan de andere kant is er in de Poisson-verdeling geen bovengrens voor deze waarden.
Poisson paste zijn beroemde distributie aanvankelijk toe op rechtszaken, maar op industrieel niveau was een van zijn vroegste toepassingen het maken van bier. Bij dit proces worden gistculturen gebruikt voor fermentatie.
Gist bestaat uit levende cellen, waarvan de populatie in de tijd varieert. Bij de productie van bier is het noodzakelijk om de benodigde hoeveelheid toe te voegen, daarom is het noodzakelijk om te weten hoeveel cellen er zijn per volume-eenheid.
Tijdens de Tweede Wereldoorlog werd de Poisson-distributie gebruikt om erachter te komen of de Duitsers daadwerkelijk vanuit Calais op Londen mikten, of gewoon willekeurig schoten. Dit was belangrijk voor de geallieerden om te bepalen hoe goed de technologie beschikbaar was voor de nazi's..
De toepassingen van de Poisson-verdeling verwijzen altijd naar tellingen in de tijd of tellingen in de ruimte. En aangezien de kans op voorkomen klein is, staat het ook bekend als de 'wet van zeldzame gebeurtenissen'.
Hier is een lijst met evenementen die in een van deze categorieën vallen:
-Registratie van de deeltjes in een radioactief verval, die net als de groei van gistcellen, een exponentiële functie is.
-Aantal bezoeken aan een bepaalde website.
-Aankomst van mensen in een rij om te betalen of bijgewoond te worden (wachtrijtheorie).
-Aantal auto's dat een bepaald punt op een weg passeert, gedurende een bepaald tijdsinterval.
-Mutaties in een bepaalde DNA-streng na blootstelling aan straling.
-Aantal meteorieten met een diameter groter dan 1 m dat in een jaar is gevallen.
-Defecten per vierkante meter stof.
-Aantal bloedcellen in 1 kubieke centimeter.
-Bellen per minuut naar een telefooncentrale.
-Chocoladeschilfers aanwezig in 1 kg cakebeslag.
-Aantal bomen besmet door een bepaalde parasiet in 1 hectare bos.
Merk op dat deze willekeurige variabelen het aantal keren vertegenwoordigen dat een gebeurtenis plaatsvindt gedurende een vaste tijdsperiode (oproepen per minuut naar de telefooncentrale), of een bepaald gebied in de ruimte (defecten van een stof per vierkante meter.
Deze gebeurtenissen zijn, zoals reeds is vastgesteld, onafhankelijk van de tijd die is verstreken sinds de laatste gebeurtenis..
De Poisson-verdeling is een goede benadering van de binominale verdeling zolang:
-De steekproefomvang is groot: n ≥ 100
-Waarschijnlijkheid p is weinig: p ≤ 0,1
- μ is in de volgorde van: np ≤ 10
In dergelijke gevallen is de Poisson-verdeling een uitstekend hulpmiddel, aangezien de binominale verdeling in deze gevallen moeilijk toe te passen kan zijn..
Een seismologische studie wees uit dat er in de afgelopen 100 jaar 93 grote aardbevingen over de hele wereld waren, minstens 6,0 op de schaal van Richter -logaritmisch-. Stel dat de Poisson-verdeling in dit geval een geschikt model is. Vind:
a) Het gemiddeld voorkomen van grote aardbevingen per jaar.
b) Ja P (y) is de waarschijnlijkheid van voorkomen Y aardbevingen tijdens een willekeurig gekozen jaar, vind de volgende waarschijnlijkheden:
P.(0), P.(1), P. (twee), P. (3), P. (4), P. (5), P. (6) en P. (7).
c) De echte resultaten van het onderzoek zijn de volgende:
- 47 jaar (0 aardbevingen)
- 31 jaar (1 aardbevingen)
- 13 jaar (2 aardbevingen)
- 5 jaar (3 aardbevingen)
- 2 jaar (4 aardbevingen)
- 0 jaar (5 aardbevingen)
- 1 jaar (6 aardbevingen)
- 1 jaar (7 aardbevingen)
Hoe verhouden deze resultaten zich tot die verkregen in deel b? Is de Poisson-verdeling een goede keuze om deze gebeurtenissen te modelleren?
a) Aardbevingen zijn gebeurtenissen waarvan de waarschijnlijkheid p het is klein en we denken aan een beperkte periode van een jaar. Het gemiddelde aantal aardbevingen is:
μ = 93/100 aardbevingen / jaar = 0,93 aardbevingen per jaar.
b) Om de gevraagde kansen te berekenen, worden waarden vervangen in de formule die aan het begin wordt gegeven:
y = 2
μ = 0,93
e = 2,71828
Het is behoorlijk minder dan P (2).
De resultaten zijn hieronder opgesomd:
P (0) = 0,395, P (1) = 0,367, P (2) = 0,171, P (3) = 0,0529, P (4) = 0,0123, P (5) = 0,00229, P (6) = 0,000355, P (7) = 0,0000471.
We zouden bijvoorbeeld kunnen zeggen dat er een kans van 39,5% is dat er in een bepaald jaar geen grote aardbeving zal plaatsvinden. Of dat er in dat jaar 5,29% van de 3 grote aardbevingen plaatsvinden.
c) De frequenties worden geanalyseerd, vermenigvuldigd met n = 100 jaar:
39,5; 36,7; 17,1; 5,29; 1,23; 0.229; 0,0355 en 0,00471.
Bijvoorbeeld:
- Een frequentie van 39,5 geeft aan dat er in 39,5 van de 100 jaar 0 grote aardbevingen plaatsvinden, we zouden kunnen zeggen dat dit vrij dicht in de buurt ligt van het werkelijke resultaat van 47 jaar zonder enige grote aardbeving..
Laten we een ander Poisson-resultaat vergelijken met de werkelijke resultaten:
- De verkregen waarde van 36,7 betekent dat er in een periode van 37 jaar 1 grote aardbeving is. Het daadwerkelijke resultaat is dat er in 31 jaar 1 grote aardbeving heeft plaatsgevonden, een goede match met het model.
- Er worden 17,1 jaar verwacht met 2 grote aardbevingen en het is bekend dat er in 13 jaar, wat een kleine waarde is, inderdaad 2 grote aardbevingen waren.
Daarom is het Poisson-model in dit geval acceptabel.
Eén bedrijf schat dat het aantal componenten dat defect raakt voordat de 100 bedrijfsuren zijn bereikt, een Poisson-verdeling volgt. Als het gemiddelde aantal storingen in die tijd 8 is, zoek dan de volgende kansen:
a) Dat een onderdeel binnen 25 uur uitvalt.
b) Uitval van minder dan twee componenten, binnen 50 uur.
c) Uitval van ten minste drie componenten in 125 uur.
a) Het is bekend dat het gemiddelde aantal storingen in 100 uur 8 is, daarom wordt in 25 uur een kwart van de storingen verwacht, dat wil zeggen 2 storingen. Dit wordt de parameter μ.
De kans dat 1 component faalt wordt aangevraagd, de willekeurige variabele is "componenten die voor 25 uur falen" en de waarde is y = 1. Door de kansfunctie in te vullen:
De vraag is echter hoe waarschijnlijk het is dat ze zullen falen minder dan twee componenten in 50 uur, niet dat precies 2 componenten falen in 50 uur, daarom moeten we de kansen optellen dat:
-Geen enkele mislukt
-Alleen mislukken 1
P (minder dan 2 componenten falen) = P (0) + P (1)
P (minder dan 2 componenten falen) = 0,0183 + 0,0732 = 0.0915
c) Dat ze falen minstens 3 componenten in 125 uur, betekent dat er in die tijd 3, 4, 5 of meer kunnen falen.
De kans dat het voorkomt minstens een van meerdere gebeurtenissen is gelijk aan 1, minus de kans dat geen van de gebeurtenissen zal plaatsvinden.
-De gewenste gebeurtenis is dat 3 of meer componenten binnen 125 uur uitvallen
-Als de gebeurtenis niet plaatsvindt, betekent dit dat minder dan 3 componenten falen, waarvan de kans is: P (0) + P (1) + P (2)
De parameter μ van de verdeling is in dit geval:
μ = 8 + 2 = 10 storingen in 125 uur.
P (3 of meer componenten falen) = 1- P (0) - P (1) - P (2)
Niemand heeft nog op dit artikel gereageerd.