
Kenmerken van discrete kansverdelingen, oefeningen
De discrete kansverdelingen ze zijn een functie die aan elk element van X (S) = x1, x2,…, xi,… toekent, waarbij X een bepaalde discrete willekeurige variabele is en S de steekproefruimte is, de waarschijnlijkheid dat de gebeurtenis plaatsvindt. Deze functie f van X (S) gedefinieerd als f (xi) = P (X = xi) wordt ook wel de waarschijnlijkheidsmassafunctie genoemd.
Deze massa aan kansen wordt doorgaans in tabelvorm weergegeven. Omdat X een discrete willekeurige variabele is, heeft X (S) een eindig aantal gebeurtenissen of een telbare oneindigheid. Onder de meest voorkomende discrete kansverdelingen hebben we de uniforme verdeling, de binominale verdeling en de Poisson-verdeling.
Artikel index
- 1 Kenmerken
- 2 soorten
- 2.1 Uniforme verdeling over n punten
- 2.2 Binominale distributie
- 2.3 Poisson-verdeling
- 2.4 Hypergeometrische distributie
- 3 Opgeloste oefeningen
- 3.1 Eerste oefening
- 3.2 Tweede oefening
- 3.3 Derde oefening
- 3.4 Derde oefening
- 4 referenties
Kenmerken
De kansverdelingsfunctie moet aan de volgende voorwaarden voldoen:
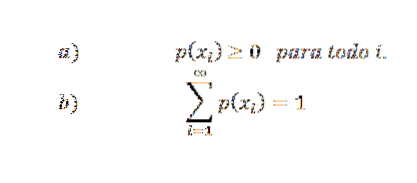
Bovendien, als X slechts een eindig aantal waarden aanneemt (bijvoorbeeld x1, x2, ..., xn), dan p (xi) = 0 als i> ny, wordt daarom de oneindige reeks van voorwaarde b een eindige reeks.
Deze functie vervult ook de volgende eigenschappen:
Laat B een gebeurtenis zijn die is gekoppeld aan de willekeurige variabele X. Dit betekent dat B zich in X (S) bevindt. Stel in het bijzonder dat B = xi1, xi2,…. Daarom:
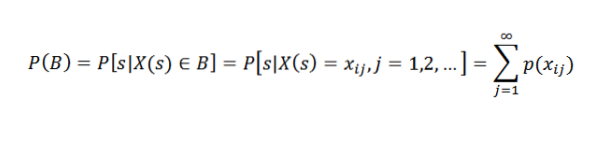
Met andere woorden: de kans op een gebeurtenis B is gelijk aan de som van de waarschijnlijkheden van de individuele uitkomsten geassocieerd met B.
Hieruit kunnen we concluderen dat als a < b, los sucesos (X ≤ a) y (a < X ≤ b) son mutuamente excluyentes y, además, su unión es el suceso (X ≤ b), por lo que tenemos:
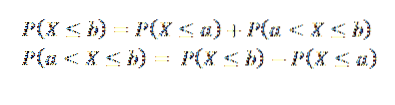
Types
Uniforme verdeling over n punten
Een willekeurige variabele X volgt een verdeling die wordt gekenmerkt door uniform te zijn op n punten als aan elke waarde dezelfde kans wordt toegekend. Zijn waarschijnlijkheidsmassafunctie is:
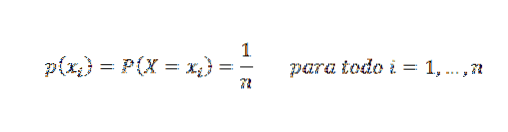
Stel dat we een experiment hebben dat twee mogelijke uitkomsten heeft, dan kan het de worp zijn van een munt waarvan de mogelijke uitkomsten kop of munt zijn, of de keuze van een geheel getal waarvan het resultaat een even of een oneven getal kan zijn; dit type experiment staat bekend als Bernoulli-tests.
Over het algemeen worden de twee mogelijke uitkomsten succes en mislukking genoemd, waarbij p de kans op succes is en 1-p de kans op mislukking. We kunnen de kans op x successen bepalen in n Bernoulli-tests die onafhankelijk van elkaar zijn met de volgende verdeling.
Binominale distributie
Het is de functie die de kans vertegenwoordigt om x successen te behalen in n onafhankelijke Bernoulli-tests, waarvan de kans op succes p is. Zijn waarschijnlijkheidsmassafunctie is:
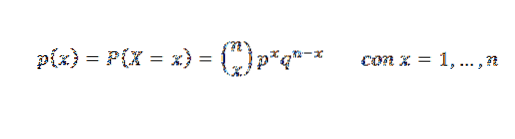
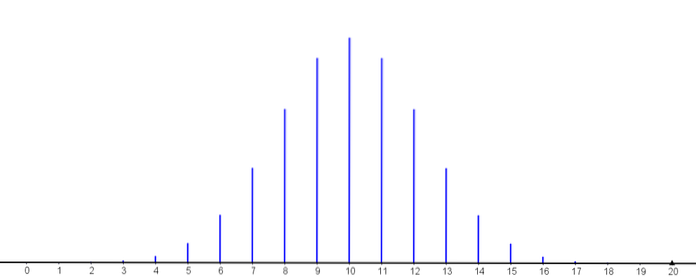
De volgende grafiek geeft de kans-massafunctie weer voor verschillende waarden van de parameters van de binominale verdeling.
De volgende verdeling dankt zijn naam aan de Franse wiskundige Simeon Poisson (1781-1840), die het bekwam als de limiet van de binominale verdeling.
Poisson-verdeling
Een willekeurige variabele X zou een Poisson-verdeling van parameter λ hebben wanneer deze de positieve gehele getallen 0,1,2,3 kan aannemen, ... met de volgende waarschijnlijkheid:
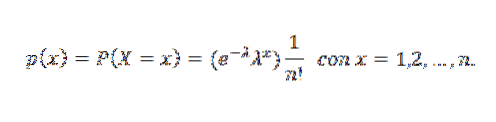
In deze uitdrukking is λ het gemiddelde aantal dat overeenkomt met het aantal keren dat de gebeurtenis voorkomt voor elke tijdseenheid, en x is het aantal keren dat de gebeurtenis voorkomt.
Zijn waarschijnlijkheidsmassafunctie is:
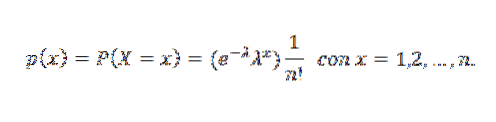
Vervolgens een grafiek die de kansmassafunctie voor verschillende waarden van de parameters van de Poisson-verdeling weergeeft.
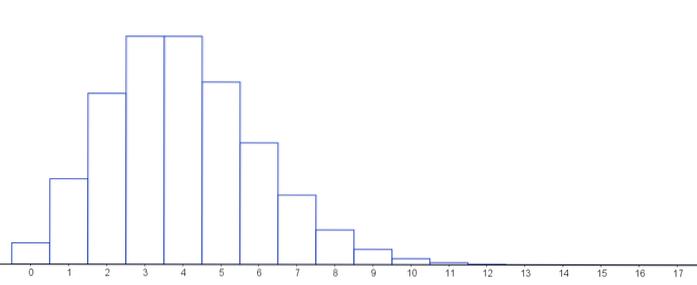
Merk op dat, zolang het aantal successen laag is en het aantal tests uitgevoerd op een binominale verdeling hoog is, we deze verdelingen altijd kunnen benaderen, aangezien de Poisson-verdeling de limiet is van de binominale verdeling..
Het belangrijkste verschil tussen deze twee verdelingen is dat, hoewel de binominale verdeling afhangt van twee parameters - namelijk n en p-, de Poisson alleen afhangt van λ, wat ook wel de intensiteit van de verdeling wordt genoemd..
Tot dusver hebben we het alleen gehad over kansverdelingen voor gevallen waarin de verschillende experimenten onafhankelijk van elkaar zijn; dat wil zeggen, wanneer het resultaat van het ene niet wordt beïnvloed door een ander resultaat.
Als er experimenten zijn die niet onafhankelijk zijn, is de hypergeometrische verdeling erg handig.
Hypergeometrische distributie
Laat N het totale aantal objecten van een eindige verzameling zijn, waarvan we k op de een of andere manier kunnen identificeren, en zo een deelverzameling K vormen, waarvan het complement wordt gevormd door de resterende N-k-elementen.
Als we willekeurig n objecten kiezen, heeft de willekeurige variabele X die het aantal objecten vertegenwoordigt dat in die keuze bij K hoort een hypergeometrische verdeling van parameters N, n en k. Zijn waarschijnlijkheidsmassafunctie is:
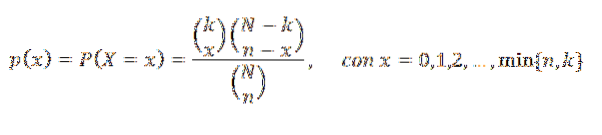
De volgende grafiek geeft de kans-massafunctie weer voor verschillende waarden van de parameters van de hypergeometrische verdeling.
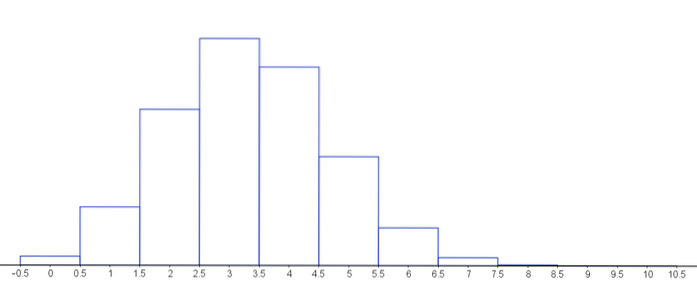
Opgeloste oefeningen
Eerste oefening
Stel dat de kans dat een radiobuis (geplaatst in een bepaald type apparatuur) meer dan 500 uur zal werken 0,2 is. Als er 20 buizen worden getest, wat is dan de kans dat precies k hiervan meer dan 500 uur zullen draaien, k = 0, 1,2, ..., 20?
Oplossing
Als X het aantal buisjes is dat meer dan 500 uur werkt, gaan we ervan uit dat X een binominale verdeling heeft. Dan
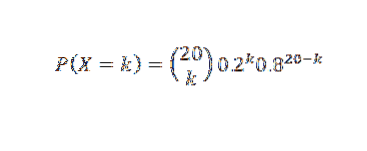
En dus:

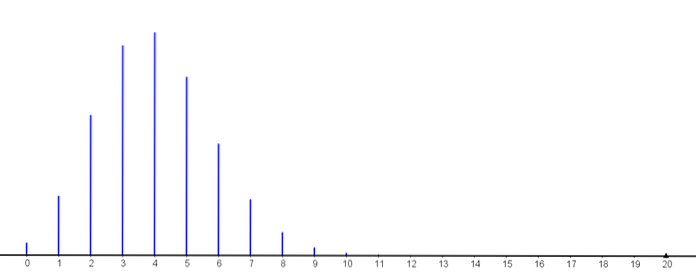
Voor k≥11 zijn de kansen kleiner dan 0,001
We kunnen dus zien hoe de kans dat k van deze meer dan 500 uur werken toeneemt, totdat het zijn maximale waarde bereikt (met k = 4) en dan begint af te nemen..
Tweede oefening
Een munt wordt 6 keer gegooid. Als het resultaat duur is, zullen we zeggen dat het een succes is. Wat is de kans dat er precies twee koppen naar boven komen??
Oplossing
Voor dit geval hebben we n = 6 en zowel de kans op succes als op mislukking is p = q = 1/2
Daarom is de kans dat twee koppen worden gegeven (dat wil zeggen, k = 2)
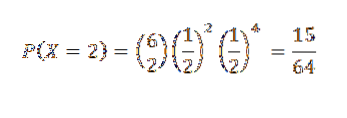
Derde oefening
Wat is de kans om minstens vier hoofden te vinden?
Oplossing
Voor dit geval hebben we dat k = 4, 5 of 6
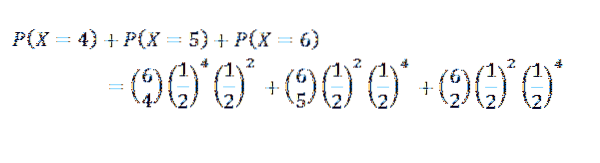
Derde oefening
Stel dat 2% van de artikelen die in een fabriek worden geproduceerd, defect is. Zoek de kans P dat er drie defecte items zijn in een steekproef van 100 items.
Oplossing
Voor dit geval zouden we de binominale verdeling voor n = 100 en p = 0,02 kunnen toepassen, met als resultaat:
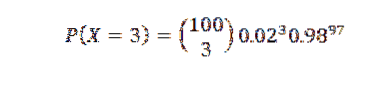
Omdat p echter klein is, gebruiken we de Poisson-benadering met λ = np = 2. A) Ja,
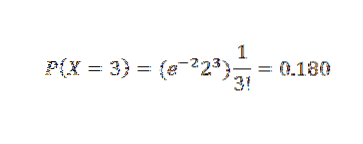
Referenties
- Kai Lai Chung. Elementaire waarschijnlijkheidstheorie met stochastische processen. Springer-Verlag New York Inc.
- Kenneth.H. Rosen Discrete wiskunde en haar toepassingen. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Waarschijnlijkheid en statistische toepassingen. S.A. MEXICAANSE ALHAMBRA.
- Seymour Lipschutz Ph.D. 2000 opgeloste problemen van discrete wiskunde. McGRAW-HILL.
- Seymour Lipschutz Ph.D. Theorie en waarschijnlijkheidsproblemen. McGRAW-HILL.



Niemand heeft nog op dit artikel gereageerd.