Er wordt gezegd dat er een verlengd lichaam is rotatiesaldo wanneer de som van de koppels die erop inwerken nul is. Dit betekent niet dat het object noodzakelijkerwijs in rust is, maar eerder dat er geen netto neiging is om zijn bewegingstoestand voor een ander te veranderen..
Een object dat met constante snelheid beweegt, doet dat langs een rechte lijn en we kunnen het in rotatie-evenwicht beschouwen. Nu roteren objecten omdat er krachten op inwerken op een zodanige manier dat er een rotatie ontstaat. Het vermogen van een kracht om rotatie te produceren, genaamd koppel of torca, hangt niet alleen af van de intensiteit van de kracht, maar ook van waar deze wordt uitgeoefend.
Dit herkennen we direct als een gesloten deur geopend moet worden: er wordt nooit kracht uitgeoefend nabij de scharnieren, maar er vandaan, daarom wordt de kruk zo ver mogelijk aan de andere kant van de deur geplaatst..
De rotatieas van de deur loopt door de scharnieren. Als je erop aandringt het heel dicht bij de scharnieren te duwen, kost het veel moeite om de deur zelfs maar een klein beetje te laten bewegen..
In de literatuur wordt koppel gevonden onder verschillende namen: koppel, torsie, moment van een kracht en koppel. Ze zijn allemaal synoniem.
We moeten dus de koppels kennen die op een object inwerken om de toestand van het rotatie-evenwicht vast te stellen.
Artikel index
De toestand van het rotatie-evenwicht is:
De som van alle momenten of koppels die op een lichaam inwerken, berekend met betrekking tot elke as, moet nul zijn.
Het object in kwestie moet worden uitgerekt, aangezien deeltjes per definitie alleen translationeel evenwicht hebben.
Er kunnen krachten op het lichaam worden uitgeoefend en nog steeds een rotatie-evenwicht bestaan, zolang de krachten het niet laten draaien.
Er kan ook beweging zijn, zelfs versneld, maar altijd langs een rechte lijn, aangezien niet alle krachten het optreden van koppels veroorzaken. Deze verschijnen wanneer de krachten niet allemaal langs dezelfde actielijn werken..
Koppel wordt aangegeven met de Griekse letter τ, Aan dikgedrukt lettertype omdat het een vector is en daarom onderscheiden we het van zijn grootte of module, die een scalair is. Het hangt af van de uitgeoefende kracht F., vector r dat is gericht van de rotatie-as O naar het punt waarop de kracht wordt uitgeoefend en tenslotte vanuit de hoek tussen deze twee vectoren.
Het vectorproduct legt de juiste relatie tussen deze grootheden vast:
τ = r X F.
En de koppelmodule, aangegeven zonder vetgedrukt, is:
τ = r⋅F⋅sen θ
Waar θ de hoek tussen is r Y F.. De koppeleenheden zijn gewoon N⋅m in het internationale systeem.
In de figuur is er een steeksleutel waarmee het bedoeld is om een moer tegen de klok in (tegen de klok in) te draaien. Hiervoor wordt het met twee krachten getest F.NAAR Y F.B..
F.NAAR is dichter bij O en heeft een vector rNAAR of kortere hefboomarm, daarom produceert het niet zoveel koppel als de kracht F.B., die even groot is, maar een vector heeft rB. groter.
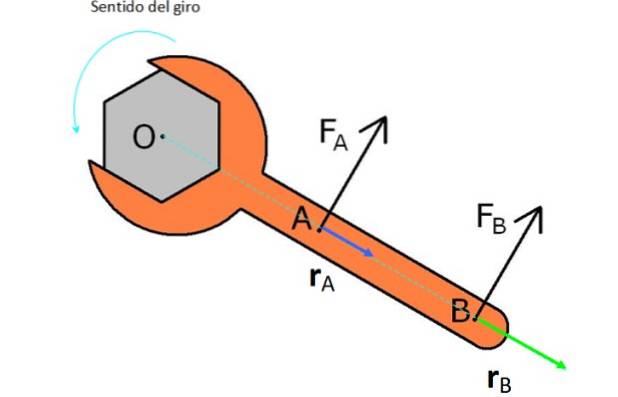
Merk op dat als u de moer met de klok mee wilt draaien, u de krachten in de tegenovergestelde richting moet uitoefenen zoals ze in de afbeelding worden weergegeven.
Aangezien het koppel het resultaat is van het kruisproduct tussen de kracht- en positievectoren, en deze zich in het vlak van de sleutel bevinden, moet het koppel een vector zijn die loodrecht op dat vlak staat, dat wil zeggen gericht naar de lezer of naar de binnenkant van de sleutel. bladzijde.
Volgens afspraak is het koppel positief als het tegen de klok in draait en negatief als het met de klok mee draait..
De richting en het gevoel van het resulterende koppel kunnen gemakkelijk worden bepaald door de rechterhandregel die hieronder wordt weergegeven:
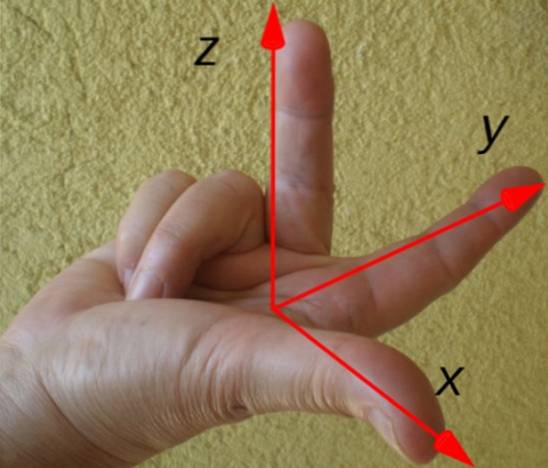
De wijsvinger wijst volgens de positievector r, middelvinger naar sterkte F. en de duim wijst de richting en het gevoel van koppel aan τ. In dit voorbeeld is het koppel gericht langs de x-as, volgens de tekening van de coördinaatassen.
Als koppels op een lichaam inwerken τ1, τtwee, τ3 ... τik, het netto of resulterende koppel τn is de vectorsom van alle:
τn = τ1+ τtwee + τ3 + τik
Met sommatie-notatie blijft het:
τn = τik
De evenwichtstoestand wordt wiskundig als volgt uitgedrukt:
τn 0
O goed:
τik 0
Waar het koppel τ, met betrekking tot een bepaalde as O, wordt deze berekend door:
τ = r X F.
En wiens omvang is:
τ = r⋅F⋅sen θ
-Bij mens en dier is gewicht een kracht die koppel en spin en vallen kan veroorzaken.
Mensen behouden over het algemeen een zodanige houding dat ze hen tijdens het lopen in rotatiebalans houden, tenzij ze sportactiviteiten beoefenen, zoals turnen, schaatsen of sporten in het algemeen..
-Twee jongens die erin slaagden horizontaal te blijven in de rocker of omhoog en omlaag zijn in rotatie-evenwicht.
-Wanneer de balanspannen in balans zijn, bevindt het systeem zich in rotatie-evenwicht.
-Borden en verkeerslichten die op straten en lanen hangen, zijn ook in rotatie-evenwicht. Als de kabels waarmee ze worden vastgehouden, breken, gaat dit evenwicht verloren en blijft het bord hangen of vallen..
-Hangbruggen zoals de Golden Gate in San Francisco en de brug in figuur 1.
De steunbalk die in de afbeelding wordt getoond, is erg licht. De kracht die wordt uitgeoefend door de ondersteuning is F. en bij extreem rechts wordt kracht uitgeoefend NAAR.
Er wordt gevraagd om de grootte van deze krachten te berekenen, aangezien het systeem in translatie- en rotatie-evenwicht is.
Omdat het systeem niet beweegt, wordt de sommatie van krachten geannuleerd. Ze zijn allemaal verticaal en kunnen worden bewerkt met de grootheden. De positieve richting is naar boven en de negatieve richting is naar beneden, dus:
F - 80 - A = 0
Nu wordt de conditie van het rotatie-evenwicht toegepast, waarvoor we een willekeurige rotatieas moeten kiezen. In dit geval wordt uiterst rechts gekozen, zodat de vector rNAAR is nul, op deze manier wordt het koppel uitgeoefend door NAAR, maar alleen die van F. en de kracht van links.
Het koppel geproduceerd door F. is, volgens de rechterhandregel en het getoonde coördinatensysteem:
τF. rF. X F. = 0,9 F (-k) N.m
Het is naar de binnenkant van het scherm gericht en heeft een negatief teken. Terwijl het koppel geproduceerd door de 80 N-kracht is:
τ = 80 x 1,20 (k) N⋅m = 96 (k) N⋅m
Dit koppel wordt van het scherm weggeleid en krijgt een positief teken. Hoe er een rotatie-evenwicht is:
96 - 0.9⋅F = 0
De omvang van F. het is:
F = (96 / 0,9) N = 106,7 N
En aangezien het systeem in translationeel evenwicht is, wordt de som van de krachten opgeheven. Dit stelt ons in staat om de grootte van op te lossen NAAR
F - EEN - 80 N = 0
Daarom:
A = 106,7 - 80 N = 26,7 N.
Niemand heeft nog op dit artikel gereageerd.