EEN vectoriële ruimte is een niet-lege set V.of, v, w,, waarvan de elementen vectoren zijn. Met hen worden enkele belangrijke operaties uitgevoerd, waaronder de volgende opvallen:
- Som tussen twee vectoren u + v welke resultaten z, die bij de set hoort V..
- Vermenigvuldiging van een reëel getal α met een vector v α v wat geeft een andere vector Y die behoort tot V..
Om een vector aan te duiden, gebruiken we vetgedrukte (v is een vector), en voor scalairen of cijfers Griekse letters (α is een getal).
Artikel index
Om een vectorruimte te geven, moet aan de volgende acht axioma's worden voldaan:
1-schakelbaar: of +v v +of
2-overgangsgevoeligheid: of + v + w of + v + w
3-Bestaan van de nulvector 0 zoals dat 0 + v v
4-Bestaan van het tegenovergestelde: het tegenovergestelde van v het is -v , net zo v + -v 0
5-distributiviteit van het product met betrekking tot de vectorsom: α ( of + v ) = αof +αv
6-Distributiviteit van het product met betrekking tot de scalaire som: (α + β)v = αv +βv
7-associativiteit van het scalaire product: α (β v) = (α β)v
8-Het nummer 1 is het neutrale element sinds: 1v v
Vectoren in het (R²) -vlak zijn een voorbeeld van een vectorruimte. Een vector in het vlak is een geometrisch object dat zowel grootte als richting heeft. Het wordt weergegeven door een georiënteerd segment dat tot het vlak behoort en met een grootte die evenredig is met de grootte ervan.
De som van twee vectoren in het vlak kan worden gedefinieerd als de geometrische translatieoperatie van de tweede vector na de eerste. Het resultaat van de som is het georiënteerde segment dat begint vanaf de oorsprong van het eerste en het puntje van het tweede bereikt.
In de figuur is te zien dat de som in R² commutatief is.
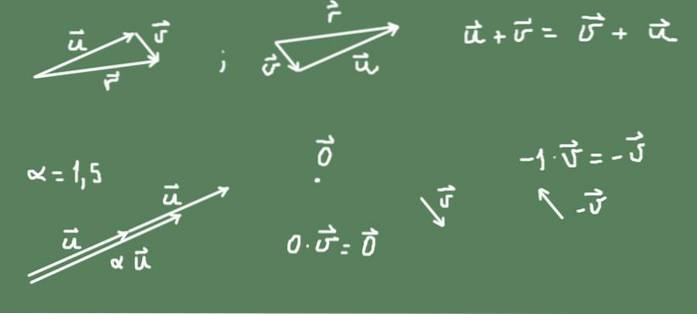
Het product van een getal α en een vector wordt ook gedefinieerd. Als het getal positief is, wordt de richting van de originele vector behouden en is de grootte α maal de originele vector. Als het getal negatief is, is de richting het tegenovergestelde en is de grootte van de resulterende vector de absolute waarde van het getal.
De vector die tegenover elke vector staat v het is -v = (- 1) v.
De nulvector is een punt in het R²-vlak en het getal nul keer een vector resulteert in de nulvector.
Alles wat gezegd is, wordt geïllustreerd in figuur 2.
Set P. van alle polynomen van graad kleiner dan of gelijk aan twee, inclusief graad nul, vormen een verzameling die voldoet aan alle axioma's van een vectorruimte.
Laat het polynoom P (x) = a x² + b x + c en Q (x) = d x² + e x + f
De som van twee polynomen wordt gedefinieerd: P (x) + Q (x) = (a + d) x² + (b + e) x + (c + f)
De som van veeltermen die bij de verzameling horen P. is commutatief en transitief.
De nulpolynoom die bij de verzameling hoort P. is degene waarvan alle coëfficiënten gelijk zijn aan nul:
0 (x) = 0 x² + 0 x + 0
De som van een scalair α door een polynoom wordt gedefinieerd als: α P (x) = α ∙ a x² + α ∙ b x + α ∙ c
Het tegenovergestelde polynoom van P (x) is -P (x) = (-1) P (x).
Uit al het bovenstaande volgt dat de set P. van alle polynomen met een graad kleiner dan of gelijk aan twee, is een vectorruimte.
Set M. van alle matrices van m rijen x n kolommen waarvan de elementen reële getallen zijn, vormen een reële vectorruimte, met betrekking tot de bewerkingen van optellen van matrices en product van een getal door een matrix.
De verzameling F van continue functies van reële variabele, vormt een vectorruimte, aangezien het mogelijk is om de som van twee functies te definiëren, de vermenigvuldiging van een scalair met een functie, de nulfunctie en de symmetrische functie. Ze vervullen ook de axioma's die een vectorruimte kenmerken.
De basis van een vectorruimte wordt gedefinieerd als een reeks lineair onafhankelijke vectoren zodat uit een lineaire combinatie van hen elke vector van die vectorruimte kan worden gegenereerd.
Het lineair combineren van twee of meer vectoren bestaat uit het vermenigvuldigen van de vectoren met een aantal scalair en vervolgens vectorieel optellen.
Bijvoorbeeld, in de vectorruimte van vectoren in drie dimensies gevormd door R³, wordt de canonieke basis gedefinieerd door de eenheidsvectoren (van magnitude 1) gebruikt ik, j, k.
Waar ik = (1, 0, 0); j = (0, 1, 0); k = (0, 0, 1). Dit zijn de cartesiaanse of canonieke vectoren.
Elke vector V. behorende tot R³ wordt geschreven als V. = een ik + b j + c k, wat een lineaire combinatie is van de basisvectoren ik, j, k. De scalairen of getallen a, b, c staan bekend als de cartesiaanse componenten van V..
Er wordt ook gezegd dat de basisvectoren van een vectorruimte een generatorset van de vectorruimte vormen.
De afmeting van een vectorruimte is het hoofdtelwoord van een vectorbasis voor die ruimte; dat wil zeggen, het aantal vectoren waaruit de basis bestaat.
Deze kardinaal is het maximale aantal lineair onafhankelijke vectoren van die vectorruimte, en tegelijkertijd het minimale aantal vectoren dat een generatorset van die ruimte vormt..
De bases van een vectorruimte zijn niet uniek, maar alle bases van dezelfde vectorruimte hebben dezelfde dimensie.
Een vectordeelruimte S van een vectorruimte V is een deelverzameling van V waarin dezelfde bewerkingen zijn gedefinieerd als in V en voldoet aan alle vectorruimte-axioma's. Daarom zal de deelruimte S ook een vectorruimte zijn.
Een voorbeeld van een vectorsubruimte zijn de vectoren die tot het XY-vlak behoren. Deze deelruimte is een deelverzameling van een vectorruimte met dimensionaliteit die groter is dan de verzameling vectoren die behoren tot de driedimensionale ruimte XYZ.
Een ander voorbeeld van een vectorsubruimte S1 van de vectorruimte S gevormd door alle 2 × 2 matrices met reële elementen wordt hieronder gedefinieerd:
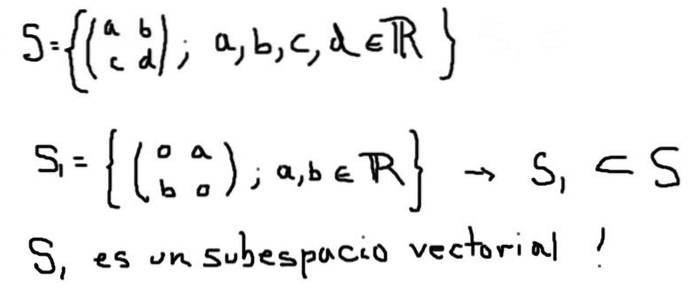
Aan de andere kant, S2 hieronder gedefinieerd, hoewel het een subset van S is, vormt geen vectorsubruimte:
Laat de vectoren zijn V1= (1, 1, 0); V2= (0, 2, 1) en V3= (0, 0, 3) in R³.
a) Laat zien dat ze lineair onafhankelijk zijn.
b) Laat zien dat ze een basis vormen in R³, aangezien elke triple (x, y, z) kan worden geschreven als een lineaire combinatie van V1, V2, V3.
c) Zoek de componenten van de triple V. = (-3,5,4) aan de basis V1, V2, V3.
Het criterium om lineaire onafhankelijkheid aan te tonen bestaat uit het opstellen van de volgende reeks vergelijkingen in α, β en γ
α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)
In het geval dat de enige oplossing voor dit systeem α = β = γ = 0 is, dan zijn de vectoren lineair onafhankelijk, anders niet.
Om de waarden van α, β en γ te verkrijgen, stellen we het volgende stelsel vergelijkingen voor:
α ∙ 1 + β ∙ 0 + γ ∙ 0 = 0
α ∙ 1 + β ∙ 2 + γ ∙ 0 = 0
α ∙ 0 + β ∙ 1 + γ ∙ 3 = 0
De eerste leidt tot α = 0, de tweede α = -2 ∙ β maar aangezien α = 0 dan β = 0. De derde vergelijking impliceert dat γ = (- 1/3) β, maar aangezien β = 0 dan γ = 0.
Er wordt geconcludeerd dat het een set lineair onafhankelijke vectoren in R³ is .
Laten we nu de triple (x, y, z) schrijven als een lineaire combinatie van V1, V2, V3.
(x, y, z) = α V1 + β V2 + γ V3 = α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)
α ∙ 1 + β ∙ 0 + γ ∙ 0 = x
α ∙ 1 + β ∙ 2 + γ ∙ 0 = y
α ∙ 0 + β ∙ 1 + γ ∙ 3 = z
Waar heb je:
α = x
α + 2 β = y
β + 3 γ = z
De eerste geeft α = x aan, de tweede β = (y-x) / 2 en de derde γ = (z- y / 2 + x / 2) / 3. Op deze manier hebben we de generatoren van α, β en γ van elk triplet van R³ gevonden
Laten we verder gaan om de componenten van de triple te vinden V. = (-3,5,4) aan de basis V1, V2, V3.
We vervangen de overeenkomstige waarden in de bovenstaande uitdrukkingen voor de generatoren.
In dit geval hebben we: α = -3; β = (5 - (- 3)) / 2 = 4; γ = (4- 5/2 + (- 3) / 2) / 3 = 0
Dat is:
(-3,5,4) = -3 (1, 1, 0) + 4 (0, 2, 1) + 0 (0, 0, 3)
Op laatst:
V. = -3 V1 + 4 V2 + 0 V3
We concluderen dat V1, V2, V3 vormen een basis in de vectorruimte R³ van dimensie 3.
Druk het polynoom P (t) = t² + 4t -3 uit als een lineaire combinatie van P1 (t) = t² -2t + 5, P2 (t) = 2t² -3t en P3 (t) = t + 3.
P (t) = X P1 (t) + Y P2 (t) + z P3 (t)
waar de getallen x, y, z moeten worden bepaald.
Het vermenigvuldigen en groeperen van termen met dezelfde graad in t geeft:
t² + 4 t -3 = (x + 2y) t² + (-2x -3y + z) t + (5x + 3z)
Dat leidt ons tot het volgende stelsel van vergelijkingen:
x + 2y = 1
-2x -3y + z = 4
5x + 3z = -3
De oplossingen van dit stelsel vergelijkingen zijn:
x = -3, y = 2, z = 4.
Dat is:
P (t) = -3 P1 (t) + 2 P2 (t) + 4 P3 (t)
Laat zien dat de vectoren v1= (1, 0, -1, 2); v2= (1, 1, 0, 1) en v3= (2, 1, -1, 1) van R⁴ zijn lineair onafhankelijk.
We combineren de drie vectoren lineair v1, v2, v3 en we eisen dat de combinatie het nulelement van R⁴ toevoegt
naar v1 + b v2 + c v3 0
Namelijk,
a (1, 0, -1, 2) + b (1, 1, 0, 1) + c (2, 1, -1, 1) = (0, 0, 0, 0)
Dit leidt ons tot het volgende stelsel van vergelijkingen:
een + b + 2 c = 0
b + c = 0
-a - c = 0
2 een + b + c = 0
Als we de eerste en de vierde aftrekken, hebben we: -a + c = 0 wat a = c impliceert.
Maar als we naar de derde vergelijking kijken, hebben we dat a = -c. De enige manier waarop a = c = (- c) geldt, is dat c 0 is en dus a ook 0 zal zijn.
a = c = 0
Als we dit resultaat in de eerste vergelijking vervangen, concluderen we dat b = 0.
Tenslotte a = b = c = 0, zodat geconcludeerd kan worden dat de vectoren v1, v2 en v3 lineair onafhankelijk zijn.
Niemand heeft nog op dit artikel gereageerd.