
De wet van Gauss

Wat is de wet van Gauss??
De de wet van Gauss stelt vast dat de flux van het elektrische veld door een denkbeeldig gesloten oppervlak evenredig is met de netto ladingswaarde van de deeltjes die zich in dat oppervlak bevinden.
Geeft de elektrische flux door een gesloten oppervlak aan als ΦEN en de netto lading die door het oppervlak wordt omsloten door Qenc, dan wordt de volgende wiskundige relatie gelegd:
ΦEN = c ∙ Qenc
Waar c is de constante van evenredigheid.
Verklaring van de wet van Gauss
Om de betekenis van de wet van Gauss te begrijpen, is het nodig om de concepten uit te leggen die in zijn verklaring zijn betrokken: elektrische lading, elektrisch veld en elektrisch veld stromen door een oppervlak..
Elektrische lading
Elektrische lading is een van de fundamentele eigenschappen van materie. Een geladen object kan een van twee soorten lading hebben: positief of negatief, hoewel de objecten normaal gesproken neutraal zijn, dat wil zeggen dat ze dezelfde hoeveelheid negatieve lading hebben als positief..
Twee geladen objecten van hetzelfde type stoten elkaar af, zelfs als er geen contact tussen is en ze zich in een vacuüm bevinden. Integendeel, als elk van de lichamen ladingen van een ander teken heeft, trekken ze elkaar aan. Dit type interactie op afstand staat bekend als een elektrische interactie..
In het internationale systeem van SI-eenheden wordt elektrische lading gemeten in coulombs (C). De negatieve elementaire ladingsdrager is de elektron met lading van -1,6 x 10-19C en de positieve elementaire ladingsdrager is het proton met een ladingswaarde +1,6 x 10-19C. Typisch geladen lichamen hebben tussen 10-9C Y 10-3C.
elektrisch veld
Een elektrisch geladen lichaam verandert de ruimte in zijn omgeving en vult deze met iets onzichtbaars, een elektrisch veld genaamd. Om te weten dat dit veld aanwezig is, is een positieve lading op het testpunt vereist.
Als de testlading op een plaats wordt geplaatst waar een elektrisch veld is, verschijnt er een kracht op in een bepaalde richting, die dezelfde is als die van het elektrische veld. Veldsterkte is de kracht op de testlading gedeeld door de hoeveelheid lading op de testlading. Dan de eenheden van het elektrische veld EN in het internationale systeem van eenheden zijn Newton Kom binnen coulomb [E] = N / C.
Positieve puntladingen produceren een naar buiten gericht radiaal veld, terwijl negatieve ladingen een radiaal naar binnen gericht veld produceren. Bovendien vervalt het veld dat wordt geproduceerd door een puntlading met de inverse van het kwadraat van de afstand tot die lading.
Elektrische veldlijnen
Michael Faraday (1791 - 1867) was de eerste die een mentaal beeld had van het elektrische veld en het zich voorstelde als lijnen die de richting van het veld volgen. In het geval van een positieve puntlading zijn deze lijnen radiaal beginnend vanuit het midden naar buiten. Waar de lijnen dichter bij elkaar zijn, is het veld intenser en minder intens waar ze verder uit elkaar staan.
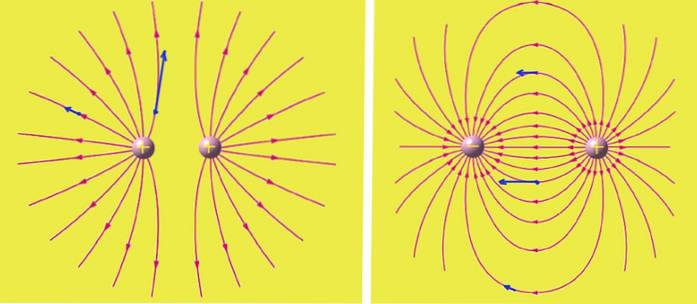
Positieve ladingen zijn de bronnen waaruit de elektrische veldlijnen komen, terwijl negatieve ladingen de putten van de lijnen zijn..
Elektrische veldlijnen sluiten zichzelf niet aan. In een reeks ladingen verlaten de lijnen de positieve ladingen en voeren de positieve in, maar ze kunnen ook oneindig reiken of komen.
Ze snijden elkaar ook niet en op elk punt in de ruimte raakt de vector van het elektrische veld de veldlijn en evenredig met de dichtheid van de lijnen daar..

Flux van elektrisch veld
Elektrische veldlijnen lijken op de stroomlijnen van een zacht stromende rivier, vandaar dat het concept van elektrische veldstroom werd geboren..
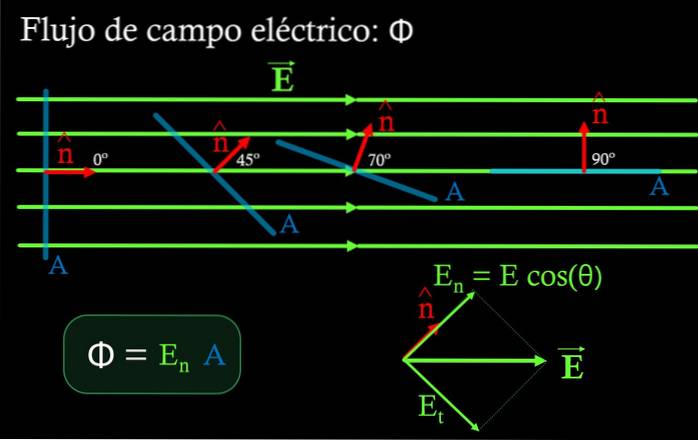
In een gebied waar het elektrische veld uniform is, is de flux Φ door een plat oppervlak het product van de normale component van het veld En naar dit oppervlak, vermenigvuldigd met het oppervlak NAAR Van hetzelfde:
Φ = En ∙ A
Onderdeel En wordt verkregen door de grootte van het elektrische veld te vermenigvuldigen met de cosinus van de hoek die wordt gevormd tussen het veld en de eenheidsnormaalvector met het oppervlak NAAR. (zie figuur 4).
Gauss 'wettoepassingen
De wet van Gauss kan worden toegepast om het elektrische veld te bepalen dat wordt geproduceerd door ladingsverdelingen met een hoge mate van symmetrie.
Elektrisch veld van een puntlading
Een puntlading produceert een radiaal elektrisch veld dat uitgaand is als de lading positief is en anders inkomend..
Door als Gaussiaans oppervlak een denkbeeldige bol met straal R te kiezen en concentrisch met de lading Q, is op alle punten op het oppervlak van die bol het elektrische veld even groot en is de richting altijd loodrecht op het oppervlak. Dus in dit geval is de flux van het elektrische veld het product van de grootte van het veld en het totale oppervlak van het bolvormige oppervlak:
Φ = E ∙ A = E ∙ 4πRtwee
Aan de andere kant stelt de wet van Gauss dat: Φ = c ∙ Q, de constante van evenredigheid is c. Bij het werken in eenheden van het internationale meetsysteem, de constante c is het omgekeerde van de permittiviteit van het vacuüm, en de wet van Gauss is als volgt geformuleerd:
Φ = (1 / εof) ∙ Q
Als we het resultaat meenemen dat is verkregen voor de stroom naar de wet van Gauss, hebben we:
E ∙ 4πRtwee = (1 / εof) ∙ Q
En voor de omvang van EN resultaat:
E = (1 / 4πεof) ∙ (Q / Rtwee
Wat volledig overeenkomt met de wet van Coulomb van het elektrische veld van een puntlading.
Opleiding
Oefening 1
Twee puntladingen liggen willekeurig binnen een Gaussiaans oppervlak S. Van één ervan is bekend dat deze een waarde heeft van +3 nC (3 nano-coulomb). Als de netto elektrische veldflux door het Gaussiaanse oppervlak 113 (N / C) m istwee, Wat wordt de waarde van de andere belasting?
Oplossing
De wet van Gauss stelt dat
ΦEN = (1 / εof) ∙ Qenc
Daarom is de netto ingesloten lading:
Qenc = ΦEN ∙ εof
Vervanging van de dataresultaten:
Qenc = 113 (N / C) mtwee ∙ 8,85 x 10-12 (C.twee m-twee N-1) = 1 x 10-9 C = 1 nC.
Maar Qenc = + Q - q, waar de positieve lading een bekende waarde van +3 nC heeft, zal de lading dus noodzakelijk -2 nC zijn.
Oefening 2
In figuur 2 is er een opstelling (aan de linkerkant) van twee positieve ladingen, elk met een waarde + q en een andere opstelling (aan de rechterkant) met een lading + q en de andere -q. Elk arrangement is ingesloten in een denkbeeldige doos met al zijn randen van 10 cm. Als | q | = 3 μC, zoek dan de netto elektrische veldflux door de doos voor elke opstelling.
Oplossing
In de eerste opstelling is de nettostroom:
ΦEN = (1 / εof) ∙ (+ q + q) = 678000 (N / C) mtwee
In de opstelling aan de rechterkant is de nettostroom door de denkbeeldige doos met het paar ladingen nul..
Referenties
- Cosenza, M. elektromagnetisme. Universiteit van de Andes.
- Díaz, R. Electrodynamics: lesnotities. Nationale universiteit van Colombia.
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 6. Elektromagnetisme. Bewerkt door Douglas Figueroa (USB).
- Jackson, J. D. Klassieke elektrodynamica. 3e. Ed Wiley.
- Tarazona, C. Inleiding tot elektrodynamica. Redactioneel Manuela Beltrán University.



Niemand heeft nog op dit artikel gereageerd.