De impulsmoment of impulsmoment is, voor rotatiebeweging, wat lineair momentum is voor translatiebeweging. Het is een vectorgrootheid die de rotatie kenmerkt van een puntdeeltje of een object dat zich uitstrekt rond een as die door een punt gaat.
Dit betekent dat wanneer het impulsmoment moet worden berekend, de rotatie-as op de juiste manier moet worden gespecificeerd.
Beginnend met een materieel massapunt m, wordt het impulsmoment aangegeven door L., lineair momentum als p en de positie van het deeltje ten opzichte van een as die door een bepaald punt O loopt is r, dan:
L. r X p
De vetgedrukte letters zijn gereserveerd voor vectorgrootheden en het kruis betekent dat het impulsmoment het vectorproduct is tussen de positievector r en het lineaire moment p van het deeltje. De vector die het resultaat is van een vectorproduct staat loodrecht op het vlak dat wordt gevormd door de deelnemende vectoren.
Dit betekent dat de richting en het gevoel van L. kan worden gevonden met behulp van de rechterhandregel voor het kruisproduct.
In het internationale systeem van eenheden SI zijn de eenheden van impulsmoment kg⋅mtwee/ s, die geen speciale naam hebben. En voor een uitgebreid lichaam, dat is samengesteld uit vele deeltjes, wordt de bovenstaande definitie gemakkelijk uitgebreid.
Artikel index
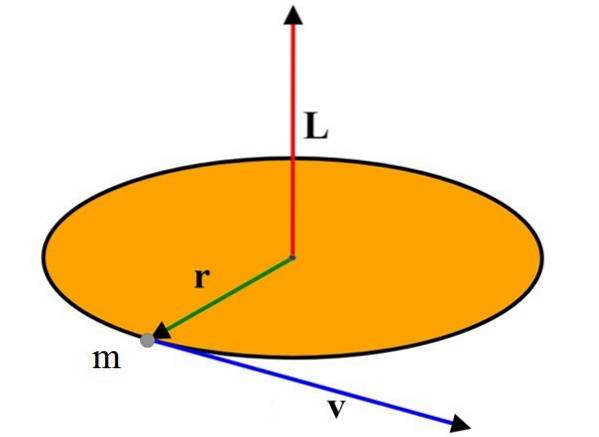
De grootte van de impulsmomentvector is volgens de definitie van het vectorproduct:
L = r⋅m⋅v⋅sen ϕ = mv (r⋅sen ϕ) = mvℓ
Waar ϕ de hoek tussen de vectoren is r Y v. Dan is ℓ = r sin ϕ de loodrechte afstand tussen de lijn van v en punt O.
Voor het geval van het deeltje dat beweegt en de omtrek beschrijft die in de bovenste afbeelding wordt weergegeven, is deze hoek 90 °, aangezien de snelheid altijd raakt aan de omtrek en dus loodrecht op de straal..
Daarom sin 90º = 1 en de grootte van L. het is:
L = m⋅r⋅v
Het traagheidsmoment van een star lichaam beschrijft de traagheid van het lichaam tegen rotatie om een bepaalde as.
Het hangt niet alleen af van de massa van het lichaam, maar ook van de afstand tot de rotatieas. Dit is gemakkelijk te begrijpen als je denkt dat het voor sommige objecten gemakkelijker is om om de ene as te draaien dan om andere..
Voor een systeem van deeltjes wordt het traagheidsmoment, aangeduid met de letter I, gegeven door:
Ik = ∑ riktwee Δmik
Waar Δmik is een kleine portie deeg en rik is de afstand tot de rotatieas. Een uitgestrekt lichaam is samengesteld uit talrijke deeltjes, daarom is het totale traagheidsmoment de som van alle producten tussen de massa en de afstand, van de deeltjes waaruit het bestaat..
Als het een uitgebreid lichaam is, verandert de sommatie in een integraal en Δm wordt een massadifferentiaal dm. De integratiegrenzen zijn afhankelijk van de geometrie van het object:
Ik = ∫M. (rtwee) dm
Het concept van traagheidsmoment hangt nauw samen met het impulsmoment van een verlengd object, zoals we hieronder zullen zien.
Beschouw een systeem van deeltjes, samengesteld uit massa's Δmik die roteert volgens een omtrek in het vlak xy, elk heeft een lineaire snelheid gerelateerd aan zijn hoeksnelheid, de laatste hetzelfde voor alle deeltjes:
vik = ωrik
Waar rik is de afstand tot de rotatieas O.Dan is de grootte van het impulsmoment:
L.ik Δmik. rik. (ωrik riktweeω Δmik
Het impulsmoment van het systeem wordt gegeven door de som:
L = ω ∑ riktwee Δmik
We identificeren snel het traagheidsmoment, zoals gedefinieerd in de vorige sectie, en daarom is de grootte van het impulsmoment als volgt:
L = Iω
Zoals we hebben gezegd dat het deeltjessysteem zich in het xy-vlak bevond, blijkt dat het impulsmoment is gericht langs de z-as, loodrecht op dat vlak. De richting wordt gegeven door die van de rotatie: het impulsmoment is positief als de rotatie tegen de klok in wordt uitgevoerd.
Een verlengd lichaam kan worden onderverdeeld in plakjes, elk met een impulsmoment gegeven door L = Iω gericht langs de z-as. Als de symmetrieas van het object samenvalt met de z-as, is er geen probleem, aangezien zelfs voor punten die niet in het xy-vlak liggen, de componenten van het impulsmoment loodrecht op die as opheffen.
Vectorieel:
L. = Ikω
Deze vergelijking is geldig voor driedimensionale objecten die rond een symmetrieas draaien.
Wanneer een netto kracht op een deeltje of lichaam inwerkt, kan zijn momentum veranderen, en dus ook zijn impulsmoment. Om te weten wanneer het varieert, gebruiken we de afgeleide, die ons de snelheid van verandering in de tijd geeft, als die er is:
De productregel toepassen op het derivaat:
De voorwaarde v x mv is nul, omdat het het product is van een vector met zichzelf, en in de tweede term vinden we de nettokracht F. = mnaar, Dus:
Het vectorproduct r X F. is niets anders dan het koppel of het nettokoppel, soms aangeduid met de Griekse letter τ of zoals M., altijd vetgedrukt, aangezien het een vectorgrootheid is. Dus, analoog aan lineair momentum, varieert het impulsmoment zolang er een netto koppel of koppel is:
dL./ dt = M.
Uit de voorgaande secties hebben we gezien dat:
dL./ dt = M.
Dat wil zeggen, het impulsmoment varieert wanneer er een netto koppel is. Als er geen nettokoppel is, dan:
dL./ dt = 0 → L. het is constant
Met andere woorden:
Initial impulsmoment = Final impulsmoment
Dit resultaat is nog steeds geldig, zelfs in het geval dat een lichaam niet star is, zoals we in de volgende voorbeelden zullen zien.
Impulsmoment is een belangrijke omvang die in veel situaties wordt onthuld, wat laat zien hoe universeel het is:
Wanneer een roterend lichaam samentrekt, neemt zijn rotatiesnelheid toe, dit is goed bekend bij schaatsers..
Dit komt door het feit dat wanneer armen en benen samentrekken, het traagheidsmoment I afneemt, aangezien de afstand tussen hun delen afneemt, maar aangezien het impulsmoment behouden blijft, om het product Iω constant te houden, moet de hoeksnelheid toenemen.
Dit geldt niet alleen bij het schaatsen, maar ook bij sporten en activiteiten waarbij het nodig is om beurten te maken, zoals duikers en trapezeartiesten in het circus..
Katten slagen er altijd in om op handen en voeten te landen als ze vallen. Hoewel ze geen momentum hebben, zorgen ze ervoor dat ze snel hun benen en staart draaien om hun rotatietraagheid te veranderen en op hun voeten te landen..
Evenzo, terwijl ze manoeuvreren, is hun impulsmoment nul, omdat hun rotatie niet continu is..
Een frisbee moet worden gegooid door hem een draai te geven zodat hij vliegt, anders valt hij. Het impulsmoment dat door de lanceerinrichting wordt geleverd, geeft de puck inderdaad voldoende stabiliteit om verder in de lucht te bewegen..
Ballen in honkbal, voetbal, basketbal en andere sporten hebben een impulsmoment. Omdat ze bolvormig zijn, hebben ze een traagheidsmoment en worden ze tijdens het spel gedraaid. Sinds het traagheidsmoment van een bol is:
I = (2/5) MRtwee
Waar M de massa van de bal is en R zijn straal, is het traagheidsmoment om een bepaalde (vaste) as:
L = (2/5) MRtweeω
De maan beweegt weg van de aarde, omdat de rotatiesnelheid van de aarde afneemt door de wrijving tussen grote watermassa's en de zeebodem.
Het aarde-maan-systeem behoudt zijn impulsmoment, dus als de aarde haar bijdrage afneemt, verhoogt de maan haar bijdrage en beweegt ze weg van de aarde..
Het eerste postulaat van Bohr's atomaire model stelt dat een elektron alleen banen bezet waar het impulsmoment een geheel veelvoud is van h / 2π, waarbij h de constante van Planck is.
Een dunne stalen staaf heeft een massa van 500 gram en een lengte van 30 cm. Het draait rond een as die door het midden gaat met een snelheid van 300 omwentelingen per minuut. Bepaal de modulus van zijn impulsmoment.
We hebben het traagheidsmoment van de staaf nodig dat verwijst naar een as die door het midden gaat. Bij het raadplegen van de tabellen van het traagheidsmoment blijkt dat:
I = (1/12) MLtwee = (1/12) × 0,5 kg x (30 × 10-twee m)twee = 3,75 × 10-3 kg.mtwee
Omdat het een verlengd lichaam is, waarvan we de hoeksnelheid kennen, gebruiken we:
L = Iω
Voordat we de hoeksnelheid of hoekfrequentie transformeren ω naar radialen / s:
ω = (300 omwentelingen / minuut) × (1 minuut / 60 seconden) x (2π radialen / omwenteling) = 10 π rad / s
Vervanging:
L = 3,75 x 10-3 kg⋅mtwee × 10 π rad / s = 0,118 kg⋅mtwee / s
Niemand heeft nog op dit artikel gereageerd.