
Eendimensionale golven wiskundige uitdrukking en voorbeelden
De eendimensionale golven Het zijn degenen die zich in een enkele richting voortplanten, ongeacht of de trilling plaatsvindt in dezelfde voortplantingsrichting of niet. Een goed voorbeeld hiervan is de golf die door een strakke snaar reist als die van een gitaar..
In een vlakke golf kruis, de deeltjes trillen in verticale richting (ze gaan op en neer, zie de rode pijl in figuur 1), maar het is eendimensionaal omdat de verstoring maar in één richting reist, de gele pijl volgend.

Eendimensionale golven komen vrij vaak voor in het dagelijks leven. De volgende sectie beschrijft enkele voorbeelden ervan en ook van golven die niet eendimensionaal zijn, om de verschillen duidelijk vast te stellen.
Artikel index
- 1 Voorbeelden van eendimensionale golven en niet-eendimensionale golven
- 1.1 Eendimensionale golven
- 1.2 Niet-eendimensionale golven
- 2 Wiskundige uitdrukking van een eendimensionale golf
- 2.1 Eendimensionale golfvergelijking
- 2.2 Uitgewerkt voorbeeld
- 3 referenties
Voorbeelden van eendimensionale golven en niet-eendimensionale golven
Eendimensionale golven
Hier zijn enkele voorbeelden van eendimensionale golven die gemakkelijk kunnen worden waargenomen:
- Een geluidspuls die door een rechte staaf gaat, aangezien het een storing is die zich over de gehele lengte van de staaf voortplant.
- Een golf die door een kanaal van water beweegt, ook al is de verplaatsing van het wateroppervlak niet evenwijdig aan het kanaal.
- Golven die zich voortplanten op een oppervlak of door een driedimensionale ruimte kunnen ook eendimensionaal zijn, zolang hun golffronten vlakken zijn die evenwijdig aan elkaar lopen en maar in één richting reizen..
Niet-eendimensionale golven
Een voorbeeld van een niet-eendimensionale golf wordt gevonden in golven die zich vormen op een stilstaand wateroppervlak wanneer een steen valt. Het is een tweedimensionale golf met een cilindrisch golffront.

Een ander voorbeeld van een niet-eendimensionale golf is de geluidsgolf die een voetzoeker opwekt door op een bepaalde hoogte te exploderen. Dit is een driedimensionale golf met bolvormige golffronten.
Wiskundige uitdrukking van een eendimensionale golf
De meest algemene manier om een eendimensionale golf uit te drukken die zich zonder verzwakking voortplant in de positieve richting van de as X en met snelheid v is, wiskundig:
y (x, t) = f (x - v.t)
In deze uitdrukking Y vertegenwoordigt de storing in de positie X Meteen t. De vorm van de golf wordt bepaald door de functie F.. De golffunctie die wordt getoond in figuur 1 is bijvoorbeeld: y (x, t) = cos (x - v t) en het golfbeeld komt overeen met het moment t = 0.
Een golf als deze, beschreven door een cosinus- of sinusfunctie, wordt genoemd harmonische golf. Hoewel het niet de enige golfvorm is die er bestaat, is het van het grootste belang, omdat elke andere golf kan worden weergegeven als een superpositie of een som van harmonische golven. Het gaat over het bekende Stelling van Fourier, zo gebruikt om allerlei soorten signalen te beschrijven.
Wanneer de golf in de negatieve richting van de x-as reist, verandert deze eenvoudig v voor -v in argument, verlaten:
y (x, t) = g (x + v t)
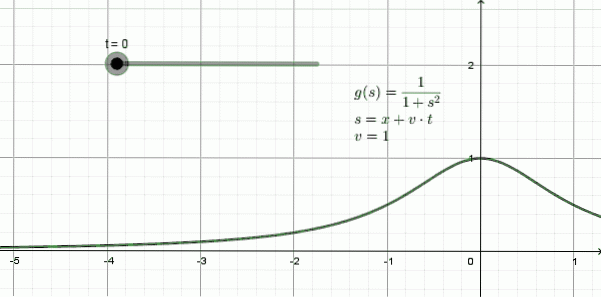
Figuur 3 toont de animatie van een golf die naar links beweegt: het is een vorm die een functie wordt genoemd lorentziana en haar wiskundige uitdrukking is:
y (x, t) = 1 / (1 + (x + 1t)twee
In dit voorbeeld is de voortplantingssnelheid v = 1, -een ruimte-eenheid voor elke tijdseenheid-.
Eendimensionale golfvergelijking
De golfvergelijking is een partiële afgeleide vergelijking, waarvan de oplossing natuurlijk een golf is. Het legt de wiskundige relatie vast tussen het ruimtelijke deel en het tijdelijke deel ervan, en heeft de vorm:

Uitgewerkt voorbeeld
Het volgende is de algemene uitdrukking y (x, t) voor een harmonische golf:
y (x, t) = EENcos (kx ± ωt + θo)
a) Beschrijf de fysieke betekenis van de parameters A, k, ω Y θo.
b) Welke betekenis hebben de ± tekens in het cosinusargument?
c) Controleer of de gegeven uitdrukking inderdaad de oplossing is van de golfvergelijking uit de vorige sectie en zoek de snelheid v voortplanting.
Oplossing voor)
De kenmerken van de golf zijn te vinden in de volgende parameters:
-NAAR vertegenwoordigt de amplitude of "golfhoogte".
-wat zit er in wave nummer en is gerelateerd aan de golflengte λ door k = 2π / λ.
-ω is de fhoekfrequentie en is gerelateerd aan de periode T golf oscillatie door
ω = 2π / T.
-θo is de begin fase, die gerelateerd is aan het startpunt van de golf.
Oplossing b)
Een negatief teken wordt genomen als de golf in de positieve richting van de X-as beweegt en een positief teken anders..
Oplossing c)
Controleer of de gegeven uitdrukking een oplossing is van de golfvergelijking is eenvoudig: de partiële afgeleide van de functie wordt genomen y (x, t) met betrekking tot x tweemaal, gedeeltelijk opnieuw afgeleid met betrekking tot t tweemaal, en vervolgens beide resultaten combineren om een gelijkheid te verkrijgen:
Tweede afgeleide met betrekking tot x: ∂tweey / ∂xtwee= -Ktwee. NAARcos (kx ± ωt + θo)
Tweede afgeleide met betrekking tot t: ∂tweej / ∂ttwee= -Ωtwee. NAARcos (kx ± ωt + θo)
Deze resultaten worden vervangen in de golfvergelijking:
-ktwee. NAARcos (kx ± ωt + θo) = (1 / vtwee) (-ωtwee. NAARcos (kx ± ωt + θo))
Zo veel NAAR omdat de cosinus vereenvoudigd is, omdat ze aan beide zijden van de gelijkheid verschijnen en het argument van de cosinus hetzelfde is, daarom reduceert de uitdrukking tot:
-ktwee = (1 / vtwee) (-ωtwee
Dat maakt het mogelijk om een vergelijking te maken voor v wat betreft ω Y k
vtwee ωtwee / ktwee
v = ω / k
Referenties
- E-educatief. Vergelijking van eendimensionale harmonische golven. Hersteld van: e-ducativa.catedu.es
- De hoek van de natuurkunde. Wave lessen. Hersteld van: fisicaparatontos.blogspot.com.
- Figueroa, D. 2006. Golven en kwantumfysica. Serie: Physics for Science and Engineering. Bewerkt door Douglas Figueroa. Simon Bolivar Universiteit. Caracas, Venezuela.
- Fysica Lab. Golfbeweging. Hersteld van: fisicalab.com.
- Peirce, A. Lezing 21: De eendimensionale golfvergelijking: D'Alembert's oplossing. Hersteld van: ubc.ca.
- Wave vergelijking. Hersteld van: en.wikipedia.com



Niemand heeft nog op dit artikel gereageerd.